Οι πανελλήνιες του '11 είναι πλέον παρελθόν! Σε λίγο καιρό τα άτομα της Β λυκείου θ' αρχίσουνε προετοιμασία. Σ' αυτή την προσπάθειά τους πρέπει να' μαστε σύμμαχοι εμείς οι πλέον "παλιοί", μιας και όλοι έχουμε περάσει το "λούκι" αυτό. Μέσα απ' αυτό το site μπορούμε να βοηθήσουμε ανεβάζοντας ασκήσεις, είτε δική μας επινόησης είτε ασκήσεις που έχουμε πετύχει στο ιντερνετ και έχουνε αυτό το ... κάτι παραπάνω που τις κάνει ξεχωριστές.
Επειδή το προηγούμενο θέμα είναι τεράστιο και η αναζήτηση ασκήσεων στους μιγαδικούς (1ο κομμάτι ύλης) είναι χρονοβόρα (και ως γνωστόν χρόνος ελεύθερος δεν υπάρχει), προτείνω να ξεκινήσουμε ένα θέμα και με τον καιρό να φτιάχνουμε ένα pdf ή ένα αρχείο που να περιέχει όλες τις ασκήσεις που θα μαζευτούν, διευκολύνοντας τη μελέτη των παιδιών.
Αν η Ο.Δ κρίνει ότι είναι περιττό θέμα, ας το μετακινήσει στο παλιό ή να κλείσει το παλιό καλύτερα. :p
Ξεκινάω εγώ λοιπόν με μια άσκηση που έφτιαξα σήμερα στους μιγαδικούς, όση ώρα περίμενα να γίνει το φαγητό

Άσκηση 1
Έστω z οι μιγαδικοί αριθμοί για τους οποίους ισχύει:
i+3)^2=(3-z+Im(z)i)(3+z-Im(z)i) )
Α. Να αποδείξετε ότι οι εικόνες των μιγαδικών z ανήκουν σε κύκλο με Κ(0,3) και ρ=3
Β. Να δείξετε ότι η ευθεία
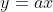
έχει ένα σταθερό σημείο τομής με τον κύκλο και ένα μεταβλητό, του οποίου να βρείτε τις συντεταγμένες. Γιατί δεν μπορούμε να πούμε ότι ο γεωμετρικός τόπος των μιγαδικών που έχουνε εικόνα το μεταβλητό σημείο που ανήκει στον κύκλο είναι ο ίδιος ο κύκλος;
Γ.Έστω
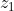
ο μιγαδικός του οποίου η εικόνα είναι το σημείο τομής του κύκλου με την
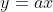
και
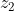
ο μιγαδικός του οποίου η εικόνα είναι το σημείο τομής του κύκλου με την
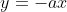
. Να βρείτε τη μέγιστη τιμή του
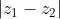
, καθώς και για ποια τιμή του α την λαμβάνει, όταν οι μιγαδικοί
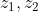
είναι μη μηδενικοί.
Το βράδυ όταν γυρίσω από το γυμναστήριο και με την προυπόθεση ότι δεν βγω για ποτό, θα ανεβάσω τη λύση σε pdf.
Άντε, καλή αρχή!