Έστω
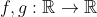
τρεις φορές παραγωγίσιμες με
-2f(1)-f(2) \geq 3g(x)-2g(1)-g(2))
. Δείξτε ότι υπάρχει
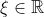
με
=g'''(\xi))
Θεωρούμε την συνάρτηση h(x)=f(x)-g(x), x ανήκει R. Επειδή οι f και g είναι 3 φορές παραγωγίσιμες στο R τότε και η h είναι 3 φορές παραγωγίσιμη στο R και ισχύει:
h΄(x)=f΄(x)-g΄(x)
h΄΄(x)=f΄΄(x)-g΄΄(x)
h΄΄΄(x)=f΄΄΄(x)-g΄΄΄(x)
για κάθε x ανήκει R
Η αρχική ανίσωση γράφεται ισοδύναμα:
3f(x)-2f(1)-f(2)>=3g(x)-2g(1)-g(2) <=> 3f(x)-3g(x)>=2f(1)-2g(1)+f(2)-g(2) <=>
<=> 3(f(x)-g(x))>=2(f(1)-g(1))+(f(2)-g(2)) <=> 3h(x)>=2h(1)+h(2) <=> h(x)>=(2/3)h(1)+(1/3)h(2) για κάθε x ανήκει R
Για x=1 έχουμε:
3h(1)>=2h(1)+h(2) <=> h(1)>=h(2)
Για x=2 έχουμε:
3h(2)>=2h(1)+h(2) <=> 2h(2)>=2h(1) <=> h(2)>=h(1)
Από τις δύο τελευταίες σχέσει προκύπτει ότι h(1)=h(2)=c όπου c ανήκει R
Η h είναι παραγωγίσιμη στο R άρα και συνεχής στο R. Η h είναι συνεχής στο [1,2], οπότε σύμφωνα με το θεώρημα μέγιστης & ελάχιστης τιμής συνεχών συναρτήσεων, υπάρχουν α,β στο [1,2] τέτοια ώστε αν m=h(α) και M=h(β) με m<=M να ισχύει m<=h(x)<=M για κάθε x στο [1,2].
Για x=1 έχουμε
m<=h(1)<=M <=> (1/3)m<=(1/3)h(1)<=(1/3)M
Για x=2 έχουμε
m<=h(2)<=M <=> (2/3)m<=(2/3)h(2)<=(2/3)M
Προσθέτοντας κατά μέλη τις 2 τελευταίες ανισότητες προκύπτει ότι:
m<=(1/3)h(1)+(2/3)h(2)<=M
Επομένως σύμφωνα με το θεώρημα ενδιαμέσων τιμών υπάρχει τουλάχιστον ένα x0 στο (1,2) τέτοιο ώστε h(x0)=(1/3)h(1)+(2/3)h(2)
Έχουμε h(x0)=(1/3)h(1)+(2/3)h(2)=(1/3)c+(2/3)c=c όπου m<=c<=M.
Άρα h(1)=h(x0)=h(2)=c
Η ανισότητα h(x)>=(2/3)h(1)+(1/3)h(2) γράφεται ισοδύναμα h(x)>=c εφόσον h(1)=h(2)=c
Ισχύει h(x)>=h(1) για κάθε x ανήκει R που σημαίνει ότι η h παρουσιάζει ολικό ελάχιστο οποτε και τοπικό ελάχιστο στο x1=1. Επειδή η h είναι ορισμένη στο R, παραγωγίσιμη στο x1=1 και παρουσιάζει τοπικό ελάχιστο στο x1=1 τότε σύμφωνα με το θεώρημα Fermat ισχύει h΄(1)=0.
Ισχύει h(x)>=h(2) για κάθε x ανήκει R που σημαίνει ότι η h παρουσιάζει ολικό ελάχιστο οποτε και τοπικό ελάχιστο στο x2=2. Επειδή η h είναι ορισμένη στο R, παραγωγίσιμη στο x2=2 και παρουσιάζει τοπικό ελάχιστο στο x2=2 τότε σύμφωνα με το θεώρημα Fermat ισχύει h΄(2)=0.
Ισχύει h(x)>=h(x0) για κάθε x ανήκει R που σημαίνει ότι η h παρουσιάζει ολικό ελάχιστο οποτε και τοπικό ελάχιστο στο x0. Επειδή η h είναι ορισμένη στο R, παραγωγίσιμη στο x0 και παρουσιάζει τοπικό ελάχιστο στο x0 τότε σύμφωνα με το θεώρημα Fermat ισχύει h΄(x0)=0.
Άρα h΄(1)=h΄(x0)=h΄(2)
Η h είναι δύο φορές παραγωγίσιμη στο [1,2] οπότε η πρώτη παράγωγος h΄ είναι παραγωγίσιμη στο (1,2) και συνεχής στο [1,2].
H h΄ είναι συνεχής στο [1,x0], παραγωγίσιμη στο (1,x0) και ισχύει h΄(1)=h΄(x0). Επομένως σύμφωνα με το θεώρημα Rolle υπάρχει τουλάχιστον ένα ξ1 στο (1,x0) τέτοιο ώστε h΄΄(ξ1)=0.
H h΄ είναι συνεχής στο [x0,2], παραγωγίσιμη στο (x0,2) και ισχύει h΄(x0)=h΄(2). Επομένως σύμφωνα με το θεώρημα Rolle υπάρχει τουλάχιστον ένα ξ2 στο (x0,2) τέτοιο ώστε h΄΄(ξ2)=0.
Άρα h΄΄(ξ1)=h΄΄(ξ2)=0
Η h είναι τρεις φορές παραγωγίσιμη στο [1,2] οπότε η δεύτερη παράγωγος h΄΄ είναι παραγωγίσιμη στο (1,2) και συνεχής στο [1,2].
H h΄΄ είναι συνεχής στο [ξ1,ξ2], παραγωγίσιμη στο (ξ1,ξ2) και ισχύει h΄΄(ξ1)=h΄΄(ξ2). Επομένως σύμφωνα με το θεώρημα Rolle υπάρχει τουλάχιστον ένα ξ στο (ξ1,ξ2) τέτοιο ώστε h΄΄΄(ξ)=0.
h΄΄΄(ξ)=0 <=> f΄΄΄(ξ)-g΄΄΄(ξ)=0 <=> f΄΄΄(ξ)=g΄΄΄(ξ)
Άρα υπάρχει τουλάχιστον ένα ξ ανήκει R τέτοιο ώστε f΄΄΄(ξ)=g΄΄΄(ξ)