Βοήθεια/Aπορίες στα Μαθηματικά Προσανατολισμού

[t00nS]

Εστω f(X) συνεχής στο [0,5] και έστω f(X) γνησίως φθίνουσα
Να δείξετε ότι υπάρχει μοναδικός ρε(0,5) ώστε: f(p)=3f(0)+2f(4)+15f(5)/20
Μέχρι το απόγευμα αν γίνεται..thx

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[rebel]

Έστω . Τότε
επειδή αφού η f είναι γνησίως φθίνουσα. Όμοια
επειδή
Από το θεώρημα Bolzano για την g στο (0,5) προκύπτει το ζητούμενο.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[antonisd95]

Λύνοντας μια άσκηση χρειάστηκε να χρησιμοποιήσω ότι η F και η F^(-1) έχουν το ίδιο ίδιος μονοτονίας.Το βιβλίο δεν λέει κάτι τέτοιο, άρα φυσικά πρέπει να το αποδείξω πριν συνεχίσω; ;;

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[JKaradakov]

Λύνοντας μια άσκηση χρειάστηκε να χρησιμοποιήσω ότι η F και η F^(-1) έχουν το ίδιο ίδιος μονοτονίας.Το βιβλίο δεν λέει κάτι τέτοιο, άρα φυσικά πρέπει να το αποδείξω πριν συνεχίσω; ;;

Yep.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[mary-blackrose]

Αν f συνεχης στο [0,3] f(0)=α και f(3)=β οπου α,β ε(0,3) να αποδειξετε οτι υπαρχει τουλαχιστον ενας αριθμος κ ε(0,3) f(κ)=κ

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Χαρουλιτα]

Αν f συνεχης στο [0,3] f(0)=α και f(3)=β οπου α,β ε(0,3) να αποδειξετε οτι υπαρχει τουλαχιστον ενας αριθμος κ ε(0,3) f(κ)=κ

Θεωρω συναρτηση g(x)=f(x)-x
Η g ειναι συνεχης στο [0,3] ως διαφορα συνεχων συναρτησεων
Τοτε: g(0)=f(0)-0=f(0)=α και g(3)=f(3)-3=β-3
Eχουμε οτι β ε (0,3) δηλαδη 0<β => -3<β-3<0 (αφαιρω και στα δυο μελη το 3)
Αρα προκυπτει οτι β-ε<0
Δηλαδη g(3)<0
Ομως α ε (0,3), αρα α>0
Επομενως g(0)g(3)<0
Απο θεωρημα Bolzano υπαρχει ενα τουλαχιστον κ ε (0,3) τετοιο ωστε g(κ)=0 => f(κ)-κ=0 => f(κ)=κ

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[mary-blackrose]

θα ηθελα μια βοηθεια στις παρακατω ασκησεις:
1)αν η f συνεχης στο [α,β] δειξτε οτι f(x)+1/(χ-α)+1/(χ-β)=0 εχει μια τουλαχιστον ριζα στο (α,β)
2)Αν για καθε χ ε [0,1] ισχυει 0=<f(x)=<1 δειξτε οτι η f(x) και η g(x)=x^2 εχουν ενα τουλαχιστον σημειο τομης με τετμημενη Χο ε [0,1]
3)εστω f,g συνεχεις συναρτησεις ωστε f(x)-g(x)=αx (α διαφορο του 0).Αν η f εχει δυο ετεροσημες ριζες ρι ,ρ2 δειξτε οτι η g εχει μια τουλαχιστον ριζα στο (ρ1,ρ2).


υ.γ στην 1) εκανα απαλοιφη των παρονομαστων...μετα εθεσα g(x)=f(x)(x-α)(χ-β)+(χ-β)+(χ-α)=0 .......επειτα ειπα g(α)=α-β ,g(β)=β-α ....αλλα πως θα βρω ποιο ειναι θετικο και ποιο αρνητικο.....;;;;

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[antonisd95]

δεν έχω πάει ακόμα στον balzano , αλλά μήπως θεωρεί δεδομένο ότι α<β αφού σου λέει διάστημα (α,β) ...νομίζω δεν έχει νόημα να σου δώσει διάστημα που να " φθίνει "

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[antwwwnis]

θα ηθελα μια βοηθεια στις παρακατω ασκησεις:
1)αν η f συνεχης στο [α,β] δειξτε οτι f(x)+1/(χ-α)+1/(χ-β)=0 εχει μια τουλαχιστον ριζα στο (α,β)
2)Αν για καθε χ ε [0,1] ισχυει 0=<f(x)=<1 δειξτε οτι η f(x) και η g(x)=x^2 εχουν ενα τουλαχιστον σημειο τομης με τετμημενη Χο ε [0,1]
3)εστω f,g συνεχεις συναρτησεις ωστε f(x)-g(x)=αx (α διαφορο του 0).Αν η f εχει δυο ετεροσημες ριζες ρι ,ρ2 δειξτε οτι η g εχει μια τουλαχιστον ριζα στο (ρ1,ρ2).


υ.γ στην 1) εκανα απαλοιφη των παρονομαστων...μετα εθεσα g(x)=f(x)(x-α)(χ-β)+(χ-β)+(χ-α)=0 .......επειτα ειπα g(α)=α-β ,g(β)=β-α ....αλλα πως θα βρω ποιο ειναι θετικο και ποιο αρνητικο.....;;;;

Στο 1: Αν πολλαπλασιάσεις τα g(a) και g(b) βγαίνει -(α-β)²<0

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[antonisd95]

αλλά ούτως ή άλλος ή το ένα θα είναι αρνητικό ή το άλλο, άρα το γινόμενο τους θα είναι < 0

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Civilara]

θα ηθελα μια βοηθεια στις παρακατω ασκησεις:
1)αν η f συνεχης στο [α,β] δειξτε οτι f(x)+1/(χ-α)+1/(χ-β)=0 εχει μια τουλαχιστον ριζα στο (α,β)

Θεωρούμε την συνάρτηση g(x)=f(x)(x-α)(x-β)+2x-α-β=f(x)(x-α)(x-β)+(x-α)+(x-β), x ανήκει [α,β] (προφανώς α<β)

Η g είναι συνεχής στο [α,β] αφού και η f είναι συνεχής στο [α,β]

g(α)=f(α)(α-α)(α-β)+2α-α-β=α-β<0
g(β)=f(β)(β-α)(β-β)+2β-α-β=β-α>0
Άρα g(α)g(β)<0

Επομένως σύμφωνα με το θεώρημα Bolzano υπάρχει τουλάχιστον ένα ξ στο (α,β) τέτοιο ώστε g(ξ)=0. Συνεπώς
g(ξ)=0 => f(ξ)(ξ-α)(ξ-β)+(ξ-α)+(ξ-β)=0 => f(ξ) +(1/(ξ-α))+(1/(ξ-β))=0

2)Αν για καθε χ ε [0,1] ισχυει 0=<f(x)=<1 δειξτε οτι η f(x) και η g(x)=x^2 εχουν ενα τουλαχιστον σημειο τομης με τετμημενη Χο ε [0,1]

Δεν δίνεται στη εκφώνηση αλλά θα θεωρήσουμε ότι η f είναι συνεχής στο [0,1].
Θεωρούμε την συνάρτηση h(x)=f(x)-g(x)=f(x)-(x^2), x ανήκει [0,1]
Η συνάρτηση h είναι συνεχής στο [0,1] αφού η f είναι συνεχής στο [0,1]
h(0)=f(0)-0^2=f(0)>=0
h(1)=f(1)-1^2=f(1)-1<=0

i) Αν f(0)=0 τότε h(0)=0 και επομένως f(0)=g(0)
ii) Αν f(1)=1 τότε h(1)=0 και επομένως f(1)=g(1)
iii) Αν h(0) διάφορο 0 και h(1) διάφορο 0 τότε h(0)>0 και h(1)<0. Επομένως h(0)h(1)<0 και επειδή η h είναι συνεχής στο [0,1] τότε σύμφωνα με το θεώρημα Bolzano υπάρχει τουλάχιστον ένα x0 τέτοιο ώστε h(x0)=0 => f(x0)=g(x0)

Άρα υπάρχει τουλάχιστον ένα x0 στο [0,1] τέτοιο ώστε f(x0)=g(x0)

3)εστω f,g συνεχεις συναρτησεις ωστε f(x)-g(x)=αx (α διαφορο του 0).Αν η f εχει δυο ετεροσημες ριζες ρι ,ρ2 δειξτε οτι η g εχει μια τουλαχιστον ριζα στο (ρ1,ρ2).

Χωρίς βλάβη της γενικότητας θεωρούμε ρ1<0<ρ2 έτσι ώστε f(ρ1)=f(ρ2)=0.
f(x)-g(x)=αx <=> g(x)=f(x)-αx, x ανήκει [ρ1,ρ2]

g(ρ1)=f(ρ1)-αρ1=-αρ1
g(ρ2)=f(ρ2)-αρ2=-αρ2
g(ρ1)g(ρ2)=(α^2)ρ1ρ2<0 αφού α^2>0 επειδή α διάφορο 0 και ρ1ρ2<0 αφού ρ1<0<ρ2

Η g είναι συνεχής στο [ρ1,ρ2] με g(ρ1)g(ρ2)<0. Άρα σύμφωνα με το θεώρημα Bolzano υπάρχει τουλάχιστον ένα ρ στο (ρ1,ρ2) τέτοιο ώστε g(ρ)=0

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Aris90]

1) Aν να αποδειχθει οτι ειναι συνεχης στο R η




δινεται η συναρτηση τετοια ωστε για καθε χΕR να ισχυει:
|f(x)-a|<=(x-a)²
ι) να αποδειξεται οτι η f ειναι συνεχης στο xo=α
ιι) να εξετασετε αν ειναι συνεχης στο χο=α η συναρτηση


παιδια λιγο βοηθεια σε αυτες τις ασκησεις pls


τι κανουμε σε αυτες τις ασκησεις?ξερει κανεις?

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Aris90]

τι κανουμε σε αυτες τις ασκησεις?ξερει κανεις?

ενταξει με την 1 τελικα ηταν πολυ ευκολη

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Civilara]

1) Aν να αποδειχθει οτι ειναι συνεχης στο R η

Για x, x0 ανήκουν R ισχύει:
f(x)-f(x0)=3(x^2)+5-3(x0^2)-5=3((x^2)-(x0^2))=3(x+x0)(x-X0)

Επομένως για x διάφορο x0 ισχύει:
g(x)=(f(x)-f(x0))/(x-x0)=3(x+x0)(x-x0)/(x-x0)=3(x+x0)

Άρα η g είναι συνεχής στο (-άπειρο,x0)U(x0,+άπειρο) ως πολυωνυμική

Γνωρίζουμε ότι g(x0)=6x0
lim(x->x0)g(x)=lim(x->x0)[3(x+x0)]=3(x0+x0)=3*2x0=6x0=g(x0)

Επομένως η g είναι συνεχής στο x0. Συνεπώς η g είναι συνεχής στο R.

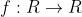
δινεται η συναρτηση τετοια ωστε για καθε χΕR να ισχυει:
|f(x)-a|<=(x-a)²
ι) να αποδειξεται οτι η f ειναι συνεχης στο xo=α
ιι) να εξετασετε αν ειναι συνεχης στο χο=α η συναρτηση

ι) |f(x)-a|<=(x-a)^2 <=> -(x-a)^2<=f(x)-a<=(x-a)^2 <=> a-(x-a)^2<=f(x)<=a+(x-a)^2

lim(x->a)[(x-a)^2]=(a-a)^2=0 => lim(x->a)[-(x-a)^2]=-lim[(x-a)^2]=-0=0
Επειδή lim(x->a)[-(x-a)^2]=lim(x->a)[(x-a)^2]=0 τότε σύμφωνα με το κριτήριο παρεμβολής τότε lim(x->a)(f(x)-a)=0 <=> lim(x->a)f(x)=a

Για x=a προκύπτει a-(a-a)^2<=f(a)<=a+(a-a)^2 <=> a<=f(a)<=a <=> f(a)=a

Επομένως lim(x->a)f(x)=f(a). Άρα η f είναι συνεχής στο a

ιι) -(x-a)^2<=f(x)-a<=(x-a)^2

Έχουμε:
lim(x->a)(x-a)=a-a=0 <=> lim(x->a-)(x-a)=lim(x->a+)(x-a)=0
lim(x->a)[-(x-a)]=-(a-a)=0 <=> lim(x->a-)[-(x-a)]=lim(x->a+)[-(x-a)]=0

Αν x<a τότε
x-a<=(f(x)-a)/(x-a)<=-(x-a)
lim(x->a-)(x-a)=lim(x->a-)[-(x-a)]=0 οπότε σύμφωνα με το κριτήριο παρεμβολής lim(x->a-)[(f(x)-a)/(x-a)]=0

Αν x>a τότε
-(x-a)<=(f(x)-a)/(x-a)<=x-a
lim(x->a+)[-(x-a)]=lim(x->a+)(x-a)=0 οπότε σύμφωνα με το κριτήριο παρεμβολής lim(x->a+)[(f(x)-a)/(x-a)]=0

lim(x->a-)[(f(x)-a)/(x-a)]=lim(x->a+)[(f(x)-a)/(x-a)]=0 <=> lim(x->a)[(f(x)-a)/(x-a)]=0

Άρα lim(x->a)g(x)=lim(x->a)[(f(x)-a)/(x-a)]=0. Γνωρίζουμε ότι g(a)=f(a)=a

Αν a=0 τότε g(0)=f(0)=0 και επομένως lim(x->0)g(x)=g(0) που σημαίνει ότι η g είναι συνεχής στο a=0.
Αν a διάφορο 0 τότε g(a)=a διάφορο lim(x->a)g(x)=0 που σημαίνει ότι η g δεν είναι συνεχής στο a για a διάφορο 0.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Mercury]

Μία ερώτηση στα γρήγορα.
Τί μπορούμε να συμπεράνουμε απο το

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[antwwwnis]

Μία ερώτηση στα γρήγορα.
Τί μπορούμε να συμπεράνουμε απο το

οτι αυτο μείον το συζυγή του μας κάνει μηδεν.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[JKaradakov]

Μία ερώτηση στα γρήγορα.
Τί μπορούμε να συμπεράνουμε απο το

Εκτός και αν θες κάτι πιο ψαγμένο.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[liofagos]

αν η f ειναι συνεχης στο [α,β] και f(a) διαφορο του μηδεν ν.δ.ο υπαρχει ενα τουλαχιστον Χο στο (α,β) τετοιο ωστε
f(Xo)/Χο-α=f(α)+f(β)/β-α

θετω g(x) αλλα δε μπορω να βρω τα προσημα των g(a) και g(b)
απο μπαρλα ειναι σελ 259 η 37..
βοηθεια..

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Giannis721]

αν η f ειναι συνεχης στο [α,β] και f(a) διαφορο του μηδεν ν.δ.ο υπαρχει ενα τουλαχιστον Χο στο (α,β) τετοιο ωστε
f(Xo)/Χο-α=f(α)+f(β)/β-α

θετω g(x) αλλα δε μπορω να βρω τα προσημα των g(a) και g(b)
απο μπαρλα ειναι σελ 259 η 37..
βοηθεια..

Κάνεις απαλοιφή παρονομαστών, τα πας όλα στο πρώτο μέλος και θεωρείς συνάρτηση
Έιναι συνεχής στο [α,β] ως πράξεις συνεχών
αφού
Bolzanoulis μετά κλπ...

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Mercury]

Εκτός και αν θες κάτι πιο ψαγμένο.

Αυτό που είπε ο Αντώνης βοήθησε.

οτι αυτο μείον το συζυγή του μας κάνει μηδεν.

Έπρεπε να αποδείξω πως ο μιγαδικός ανηκει στο R

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.