Ασκήσεις προς επίλυση στους Μιγαδικούς

[nova]

Παραθέτω μια αγαπημένη μου άσκηση στους μιγαδικούς και πιστεύω αξίζει να ασχοληθείτε!!!


Έστω οι μιγαδικοί ώστε να ικανοποιούν τις σχέσεις
και
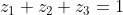
Να δείξετε ότι
ή ή

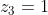
Θεωρούμε την παράσταση

Έχουμε:













Επομένως
ή ή

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 17 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Scandal]

Άσκηση Α
Η εικόνα του μιγαδικοί z κινείται στην ευθεία 3x + 4y - 60 = 0. Να βρείτε την ελάχιστη τιμή του l z-3-4i l.

Λύση: 7

Εύκολη πρέπει να 'ναι αλλά δε ξέρω πως να αξιοποιήσω την ευθεία.

Άσκηση Β
Δίνονται οι μιγαδικοί z και w οι οποίοι ικανοποιούν τις σχέσεις:
l z-3-4i l=5 και l w-6-8i l=10

α) Να βρείτε το μέγιστο μέτρο των μιγαδικών z και w.
β) Να βρείτε τη μέγιστη και την ελάχιστη τιμή του lz-wl
γ) Να βρείτε τους μιγαδικούς αριθμούς για τους οποίους η τιμή του lz-wl γίνεται μέγιστη ή ελάχιστη αντίστοιχα.

Λύσεις: α) το μέγιστο του lzl είναι 10, το μέγιστο του lwl είναι 20 β) 0<= lz-wl <=20 γ) (w1= 12+16i, z1= 0+0i) ή (w2= 0+0i και z2=0+0i)

:thanks:


-petros

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 17 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Kristal]

Άσκηση Α
Η εικόνα του μιγαδικοί z κινείται στην ευθεία 3x + 4y - 60 = 0. Να βρείτε την ελάχιστη τιμή του l z-3-4i l.

Λύση: 7

Εύκολη πρέπει να 'ναι αλλά δε ξέρω πως να αξιοποιήσω την ευθεία.

Άσκηση Β
Δίνονται οι μιγαδικοί z και w οι οποίοι ικανοποιούν τις σχέσεις:
l z-3-4i l=5 και l w-6-8i l=10

α) Να βρείτε το μέγιστο μέτρο των μιγαδικών z και w.
β) Να βρείτε τη μέγιστη και την ελάχιστη τιμή του lz-wl
γ) Να βρείτε τους μιγαδικούς αριθμούς για τους οποίους η τιμή του lz-wl γίνεται μέγιστη ή ελάχιστη αντίστοιχα.

Λύσεις: α) το μέγιστο του lzl είναι 10, το μέγιστο του lwl είναι 20 β) 0<= lz-wl <=20 γ) (w1= 12+16i, z1= 0+0i) ή (w2= 0+0i και z2=0+0i)

:thanks:


-petros

Στην πρώτη άσκηση γνωρίζεις οτι επειδή ο μιγαδικός ανήκει στην ευθεία οι συντεταγμένες του ικανοποιούν την εξίσωση...Άρα απο αυτό θα βρείς την ελάχιστη απόσταση του Ο απο την ευθεία που θα είναι και ο z(min)=[A*0+B*0+Γ]/(Ριζα(Α^2+Β^2))... Απο εκεί και πέρα θα πάρεις για την παράσταση που θέλεις τριγωνική ανισότητα και θα σπάσεις την παράσταση σε μέτρο z και σε μετρο 3+4i οποτε απο εκει θα προκύψει οτι το ελάχιστο μέτρο ειναι 7.
Για την 2η άσκηση έχεις οτι οι γεωμετρικοί τόποι είναι κύκλοι και ξέρεις ακτίνα και κέντρο άρα το μέγιστο μέτρο των μιγαδικών θα είναι η απόσταση Των κέντρων τους απο το Ο αν προσθέσεις την ακτίνα του καθενός...Για το β)ερωτημα κανε σχήμα και παίξε με την διάκεντρο και στο γ θα λύσεις σύστημα ευθείας που διέρχεται απο τα κέντρα με τους κύκλους..
Με κάθε επιφύλαξη...

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 17 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Sior_Tapas]

Έστω ο μιγαδικός αριθμός w με |w|=((|Ζ||Ζ|-{Ζ}w+Z{w})/|w|-3)-3 και |w| διάφορο του 3. Να δείξετε οτι οι εικόνες του w κινούνται στους άπειρους κύκλους με κέντρα τις εικόνες του Ζ και ακτίνα 3.

Σημείωσεις:
1) |Ζ||Ζ|=μέτρο του Ζ στο τετράγωνο
2) {Z}= Ζ συζηγής
3) {w}= w συζυγής

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 17 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[dal_kos]

Σίγουρα είναι -{z}w+z{w} η παράσταση στον αριθμητη? Γιατί κάνοντας όλες τις πράξεις, κολλάω στα πρόσημα
Βασικά πρέπει να δείξουμε ότι

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 17 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[169]

(z^2+w^2)(z^2+w^2+2zw)=0<=>
(z^2+w^2)^2+2zw(z^2+w^2)=0 <=>
(z^2+w^2)(z+w)^2=0(1)
άρα
έστω ότι (z+w)^2=0άτοπο διοτι |(z+w)^2|=1
έστω ότι z^2+w^2=0δεκτή διότι |z^2|=|w^2|
οπότε
(1)<=>0=0 που ισχύει

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 17 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[169]

(z^2+w^2)(z^2+w^2+2zw)=0
έστω ότι (z+w)^2=0άτοπο διότι |(z+w)^2|=1
έστω ότι z^2+w^2=0<=>Z^2=-w^2 μετράρεις και... |z^2|=|w^2|που ισχύει διότι |z|=|w|

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 17 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[who]

Πάρτε και μία από εμένα,
Αν ισχύει z^100+z^99+z^98+...+z+1=0, να αποδείξετε ότι z+1/z E R.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 17 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[169]

για να δω ...τι κανετε σε ενα αληθινο προβλημα

αποδείξτε οτι ο u=(z^2004-i)^2005-(i+(zσυζηγης)^2004)^2005 ειναι φανταστικος

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 17 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[mostel]

Κλασικό , αλλά ωραίο ασκησάκι.


Έχουμε:













Άρα:





Δηλαδή:





Qed!




Στέλιος

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 17 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[gossipgirl]

ενα μαθημα εχω κανει στους μιγαδικους...οποτε αποκλειεται να το λυσω...το σημειωνω ομως!

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 17 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[mostel]

Αρκεί να ζείξουμε ότι :







Stelios



PS: Το πόσταρες σε λάθος τόπικ!

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 17 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[gossipgirl]

ή μαλλον μπορεις να μου στειλεις τη λυση αν δεν ειναι κοπος;;;;;

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 17 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[gossipgirl]

να ρωτησω κατι;;;αυτο οτι u=-u δεν ειναι απο ασκηση στο βιβλιο στη β ομαδα;;;δηλ μπορουμε να το παρουμε έτοιμο;;;;;;ή κανουμε την αποδειξη;;;

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 17 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[mostel]

Η λύση είναι ουσιαστικά πιο πάνω:


Δηλαδή:





Stelios

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 17 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[mostel]

Πρέπει να κάνεις την απόδειξη! Αλλά θεωρείται από τις SOS εφαρμογές.



Στέλιος

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 17 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[gossipgirl]

Πρέπει να κάνεις την απόδειξη! Αλλά θεωρείται από τις SOS εφαρμογές.



Στέλιος

α!οκ!ευχαριστω!θα την μαθω καλα!

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 17 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[169]

το u=uσυζηγης οταν u ειναι πραγματικος θεωρηται αυτονοητη αρχη ομως το θεικο μας βιβλιο δεν την περιεχει αρα πρεπει να την αποδειξεις ομως στις ασκησεις των πανελληνιων δοθηκε οδηγια να μην λαμβανεται ως λαθος αν δεν υπαρχει η αποδειξη

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 17 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[169]

η λυση στηριζεται στο οτι η διαφορα 2 συζηγων μιγαδικων είναι φανταστικος

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 17 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[miv]

Απο τη στιγμή που δεν περιλαμβάνεται στο βιβλίο, πάντως, για μεγαλύτερη σιγουριά, όπου εφαρμόζεται πρέπει ν'αποδεικνύεται.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 17 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.