Εστω:
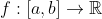
συνεχης και ισχυουν οι σχεσεις :
dx=f(a)-1 \\ \int_a^b f(x)dx<sinb-sina )
νδο
 : f(\xi)=cos{\xi} )
Μπορούμε να θεωρήσουμε συνάρτηση :
h(x) = f(x) - cosx , α <= x <= b .
Ολοκληρώνοντας αριστερά και δεξιά :
H(x) = F(x) - sinx + sinα , α <= x <= b , όπου F(x) = ∫f(x) dx απο α εως x .
H(α) = 0
H(b) = F(b) - sinb + sinα
Απο την δεύτερη συνθήκη ισχύει : F(b) < sinb - sinα => F(b) - sinb + sinα < 0 , οπότε H(b) < 0.
Εφόσον η H είναι παραγωγίσιμη στο (α,β) και συνεχής στο [α,β] , απο το ΘΜΤ υπάρχει τουλάχιστον ένα ζ Ε (α,β) τέτοιο ώστε :
H'(ζ) = h(ζ) = [H(b)-H(α)] / (b-α) = H(b)/(b-α) < 0 , διότι b>α και H(b) < 0 .
Άρα υπάρχει τουλάχιστον ένα ζ Ε (α,β) τέτοιο ώστε h(ζ) < 0 .
Έχουμε επίσης οτι : e^x - x - cosx >= e^x - x -1 .
Απο την γνωστή ανισότητα όμως : e^x >= x + 1 => e^x - x - 1 >= 0 για κάθε x E R , με την ισότητα να ισχύει μόνο για x = 0.
Το ολοκλήρωμα της ποσότητας e^x - x -1 λοιπόν σε ένα διάστημα [α,b] , όπου b > α, θα είναι πάντα θετικό.
Εφόσον η ποσότητα e^x - x - cosx είναι μεγαλύτερη ή ίση της προηγούμενης, και αυτής λοιπόν το ολοκλήρωμα σε ένα διάστημα [α,b] με b>α θα είναι πάντα θετικό. Ας ονοματίσουμε το αποτέλεσμα :
Α = ∫( e^x - x - cosx )dx > 0
Απο την πρώτη συνθήκη λοιπόν αφαιρούμε απο κάθε μέλος το cos(α) και προσθέτουμε 1 :
A + 1 - cos(α) = f(α) - cos(α) = h(α) .
Εφόσον Α > 0 και cos(α) <= 1 => 0 <= 1-cos(α), ξεκάθαρα η συνολική αριστερή ποσότητα : Α + 1 - cos(α) είναι θετική. Εν τέλει, μπορούμε να αποφανθούμε πως h(α) > 0 .
Εφόσον η h είναι συνεχής στο [α,b] ως συνάρτηση συνεχών συναρτήσεων και h(α)h(ζ) < 0 , απο το θεώρημα Bolzano υπάρχει τουλάχιστον ένα ξ Ε (α,ξ) C (α,b) τέτοιο ώστε h(ξ) = 0 . Δηλαδή f(ξ) - cosξ = 0 ή f(ξ) = cosξ .