Έστω
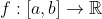
παραγωγίσιμη στο
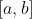
με
=(x-a)(x-b)f'(x),\,\,x \in [a,b])
. Δείξτε ότι
=0 ,\,\, x \in [a,b])
Θεωρούμε την συνάρτηση g(x)=(x-a)(x-b)=(x^2)-(a+b)x+ab, x ανήκει Dg=R. Η g είναι συνεχής στο R ως πολυωνυμική. Για την g ισχύει g(a)=g(b)=0 και g(x)<0 για a<x<b.
Θεωρούμε την συνάρτηση h(x)=1/g(x)=1/[(x-a)(x-b)] με πεδίο ορισμού Dh=(-oo,a)U(a,b)U(b,+oo). Η h είναι συνεχής στο Dh ως ρητή. Στη συνέχεια αναζητούμε πραγματικούς αριθμούς Α, Β έτσι ώστε:
h(x)=[A/(x-a)]+[B/(x-b)] για κάθε x ανήκει Dh.
Έχουμε:
1/[(x-a)(x-b)]=[A/(x-a)]+[B/(x-b)] <=> A(x-b)+B(x-a)=1 <=> (A+B)x+(-Ab-Ba)=1
Για να ισχύει η παραπάνω σχέση για κάθε x ανήκει Dh πρέπει να ισχύουν οι εξής:
A+B=0 (1)
-Ab-Ba=1 (2)
Από την (1) έχουμε:
B=-A (3)
Αντικαθιστώντας στην (2) έχουμε:
-Ab+Aa=1 <=> A(a-b)=1 <=> A=1/(a-b) <=> A=-1/(b-a)
B=-A => B=1/(b-a)
Επομένως
h(x)=[-1/(b-a)][1/(x-a)]+[1/(b-a)][1/(x-b)]=[1/(b-a)]{[1/(x-b)]-[1/(x-a)]}, x ανήκει Dh
Στη συνέχεια θα προσδιοριστεί το αόριστο ολοκλήρωμα της h στο διάστημα Δ=(a,b). Έχουμε
dx=\int \frac{1}{(x-a)(x-b)}dx=\frac{1}{b-a}\left(-\int \frac{1}{x-a}dx+\int \frac{1}{x-b}dx \right)=\frac{1}{b-a}\left(-ln|x-a|+ln|x-b| \right)+C=\frac{1}{b-a}[-ln(x-a)+ln(b-x)]+C=\frac{1}{b-a}ln\left(\frac{b-x}{x-a} \right)+C)
Θεωρούμε την συνάρτηση
=\frac{1}{b-a}ln\left(\frac{b-x}{x-a} \right)=\frac{1}{b-a}ln\left(-\frac{x-b}{x-a} \right))
με πεδίο ορισμού (α,β). Η H είναι παραγωγίσιμη και αρχική της h στο (α,β), δηλαδή:
H΄(x)=h(x) για κάθε x ανήκει (α,β)
Για κάθε x ανήκει [α,β] ισχύει f(x)=g(x)f΄(x). Επειδή g(a)=g(b)=0 έχουμε f(a)=g(a)f΄(a)=0 και f(b)=g(b)f΄(b)=0. Στη συνέχεια θα προσδιοριστεί ο τύπος της f στο (a,b). Για κάθε x ανήκει (α,β) ισχύει g(x)<0 οπότε έχουμε:
f(x)=g(x)f΄(x) <=> f(x)/g(x)=f΄(x) <=> f(x)h(x)=f΄(x) <=> f(x)H΄(x)=f΄(x) <=> f΄(x)-f(x)H΄(x)=0
Θεωρούμε την συνάρτηση F(x)=f(x)[e^(-H(x))], x ανήκει (a,b). Επειδή οι f και H είναι παραγωγίσιμες στο (a,b), οπότε η F είναι παραγωγίσιμη στο (a,b), οπότε και συνεχής στο (α,β), με παράγωγο:
F΄(x)=f΄(x)[e^(-H(x)]-f(x)H΄(x)[e^(-H(x))]=[f΄(x)-f(x)H΄(x)][e^(-H(x))]=0*[e^(-H(x))]=0
Η F είναι συνεχής και παραγωγίσιμη στο (a,b) και ισχύει F΄(x)=0 για κάθε x ανήκει (α,β). Επομένως υπάρχει σταθερά c έτσι ώστε να ισχύει F(x)=0 για κάθε x ανήκει (a,b). Άρα:
F(x)=c <=> f(x)[e^(-H(x))]=c <=> f(x)=c[e^H(x)] <=> f(x)=c{[-(x-b)/(x-a)]^[1/(b-a)]}
Επομένως f(a)=f(b)=0 και f(x)=c{[-(x-b)/(x-a)]^[1/(b-a)]} για x ανήκει (a,b).
Η f είναι παραγωγίσιμη στο (a,b) με πρώτη παράγωγο:
f΄(x)=-[c/((x-b)^2)]{[-(x-b)/(x-a)]^[(a-b+1)/(b-a)]}
Από την εκφώνηση γνωρίζουμε ότι η f είναι παραγωγίσιμη στο [a,b]. Επομένως η f είναι συνεχής στο [a,b] και παραγωγίσιμη στο (a,b).
Η f είναι συνεχής στο [a,b], παραγωγίσιμη στο (a,b) και ισχύει f(a)=f(b). Επομένως σύμφωνα με το θεώρημα του Rolle υπάρχει τουλάχιστον ένα ξ ανήκει (a,b) τέτοιο ώστε f΄(ξ)=0. Έχουμε
f΄(ξ)=-[c/((ξ-b)^2)]{[-(ξ-b)/(ξ-a)]^[(a-b+1)/(b-a)]}
Συνεπώς
f΄(ξ)=0 <=> -[c/((ξ-b)^2)]{[-(ξ-b)/(ξ-a)]^[(a-b+1)/(b-a)]}=0 <=> c=0
Άρα f(x)=0 για κάθε x ανήκει (a,b) και επειδή f(a)=f(b)=0 τότε f(x)=0 για κάθε x ανήκει [a,b].