Για μία συνάρτηση
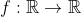
ισχύει
\right)=\alpha x+\beta,\,\,\forall x \in \mathbb{R})
όπου
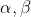
δύο δοσμένοι πραγματικοί αριθμοί με
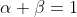
και
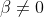
. Να αποδείξετε ότι η εξίσωση
=x)
έχει μία μοναδική ρίζα στο
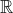
Επειδή α+β=1 τότε β=1-α και επειδή β διάφορο 0 τότε α διάφορο 1.
(i) Αν α=0 τότε β=1 και η σχέση γίνεται f(f(x))=1 για κάθε x ανήκει R. Αν η συνάρτηση f δεν είναι σταθερή τότε υπάρχουν x1, x2 με x1 διάφορο x2 ώστε f(x1) διάφορο f(x2). Τότε έχουμε:
f(x1) διάφορο f(x2) => f(f(x1)) διάφορο f(f(x2)) που είναι άτοπο αφού f(f(x1))=f(f(x2))=1
Άρα η f είναι σταθερή, δηλαδή υπάρχει c ανήκει R ώστε f(x)=c για κάθε x ανήκει R. Άρα f(f(x))=c και επειδή f(f(x))=1 για κάθε x ανήκει R τότε c=1 που σημαίνει ότι f(x)=1 για κάθε x ανήκει R.
f(x)=x => x=1
Άρα η εξίσωση f(x)=x έχει μοναδική ρίζα την x=1
(i) Αν α διάφορο 0 τότε επειδή β διάφορο 0 και β=1-α ισχύει α διάφορο 1. Άρα α ανήκει (-οο,0)U(0,1)U(1,+oo).
Ισχύει f(f(x))=αx+1-α, x ανήκει R
Θεωρούμε x1, x2 ανήκουν R με f(x1)=f(x2). Έχουμε
f(x1)=f(x2) => f(f(x1))=f(f(x2)) => αx1+1-α=αx2+1-α => αx1=αx2 => x1=x2
Άρα η f είναι 1-1.
Από την σχέση f(f(x))=αx+1-α, έχουμε:
f(f(f(x)))=f(αx+1-α), x ανήκει R
f(f(f(x)))=αf(x)+1-α, x ανήκει R
Άρα f(αx+1-α)=αf(x)+1-α για κάθε x ανήκει R
Για x=1 προκύπτει
f(α+1-α)=αf(1)+1-α => f(1)=αf(1)+1-α => αf(1)-f(1)+1-α=0 => (α-1)f(1)-(α-1)=0 => (α-1)(f(1)-1)=0 => f(1)-1=0 => f(1)=1 (α διάφορο 1)
Έστω η συνάρτηση g(x)=f(x)-x, x ανήκει R. Θεωρούμε x1, x2 με f(x1)=f(x2). Επειδή η f είναι 1-1 προκύπτει x1=x2. Από τις 2 τελευταίες σχέσεις προκύπτει f(x1)-x1=f(x2)-x2 => g(x1)=g(x2).
Επομένως η g είναι 1-1. Για x=1 έχουμε g(1)=f(1)-1=1-1=0
Άρα ο x=1 είναι ρίζα της g(x)=0 και επειδή η g είναι 1-1 τότε είναι και η μοναδική ρίζα της εξίσωσης g(x)=0 <=> f(x)=x.
Συνεπώς σε κάθε περίπτωση η εξίσωση f(x)=x έχει μοναδική λύση την x=1.