Αντε να βαλω και μια πανω στις συναρτησεις.....για να αναψουν τα αιματα.....




!!!!
1]Δινεται η συναρτηση
=\frac{1+e^x}{1+{e}^{x+1}})
(i)Να βρεθει το πεδιο ορισμου της f
(ii)Να μελετηθει η f ως προς την μονοτονια και τα ακροτατα
(iii)Να λυθει η εξισωση
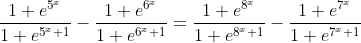
2]Δινεται η συνεχης συναρτηση
...για την οποια ισχυει οτι:

+\left|z+i \right|f(1-x)=\left|z-i \right|+\left|z+i \right|,\; z\epsilon C^*)
(i)Να δειχθει οτι ο z ειναι πραγματικος αριθμος

(ii)Να βρεθει για ποια χ ισχυει οτι
> 1)
(iii)Να αποδειξετε οτι
\;dx=1)
(iv)Να αποδειξετε οτι
\;dt+xf(x)=1)
Y.Γ: Η δευτερη ασκηση ειναι απο διαγωνισμα ΠΑΛΟΥΚΙ στο σχολειο



!!!!!
με αμφιβολιες παραθετω την λυση μου.
2]
α) θετω |z-i|=αΕR , |z+i|=βER
και εχω
α f(x) + β f(1-x) = α+β (1)
στην συνεχεια θετω 1-x=u και εχω
α f(1-u) + β f(u)= α+β
αλλαζω την μεταβλητη σε x και γινεται
α f(1-x) + β f(x) = α + β (2)
αφαιρω κατα μελη τις (1) , (2) και εχω
α f(x) - α f(1-x) + β f(1-x) - β f(x) = 0 <=>
α ( f(x) - f(1-x) ) - β ( f(x) - f(1-x) ) =0 <=>
(α-β) ( f(x) - f(1-x) ) = 0 (3)
αν f(x)-f(1-x)=0 τοτε f(x)=f(1-x) τοτε x=1/2 αφου f 1-1
αρα για x≠1/2 ειναι και f(x)-f(1-x)≠0
οποτε απο την σχεση (3) για x≠1/2 εχω
α=β αρα |z-i|=|z+i| και με λιγες πραξεις z=z' οπου z' ο συζυγης του z αρα zER
ομως επειδη ο μιγαδικος z δεν ειναι συναρτηση του x θα ισχυει για καθε xER οτι zER και |z-i|=|z+i|
β) απεδειξα οτι ειτε |z-i|=|z+i| και αφου zEC* z≠0
αρα η αρχικη γινεται
f(x)+f(1-x)=1+1
f(x)+f(1-x)=2 (4)
για x=1/2 , 2f(1/2)=2 => f(1/2)=1
αρα f(x)>1 => f(x) > f(1/2) => x>1/2
γ) βαζωντας ολοκληρωμα στην (4) με τα απαιτουμενα ακρα, σπαζωντας το ενα ολοκληρωμα και κανωντας αλλαγη μεταβλητης βγαινει το αλλο ολοκληρωμα και με λιγες πραξεις βγαινει, ας το κανουν οι μικροι
δ) για x=0 εχω 0=1 αδυνατο να το αποδειξεις :-P