Mα εμεις δεν πρεπει να φτασουμε στο εξης?:Αν χ2>χ1>0 τοτε:x1^x1 * x2^x2>(x1/2 +x2/2)^x1+x2
Από την τελευταία σχέση που ισχύει, μέσω των ισοδυναμιών φθάνει σε αυτήν που λές, στην αρχική. Πολλές φορές όταν θέλουμε να αποδείξουμε έναν ισχυρισμό, προχωράμε με ισοδυναμίες μέχρι να φθάσουμε σε κάτι που ισχύει. Τότε λόγω των ισοδυναμιών θα ισχύει ο αρχικός ισχυρισμός.
Παράδειγμα
Να δειχθεί ότι
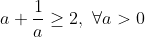
H σχέση που πρέπει να αποδειχθεί γίνεται ισοδύναμα για κάθε α>0:
^2 \geq 0)
Η τελευταία σχέση είναι αληθής άρα μέσω των ισοδυναμιών και η αρχική σχέση θα είναι αληθής.
Βοηθησε με.Επισης μπορεις να μου εξηγησεις την νοοτροπια του 1ου ερωτηματος?Τα ορια και τα λοιπα.Τα επαιξα ολιγον.
Γενικά η νοοτροπία είναι ότι αφού μου δίνουν μία ανισότητα και ψάχνω να βρω τον τύπο της συνάρτησης f(η οποία ελπίζω ότι έιναι παραγωγίσιμη κάτι που δεν αναφέρεται στην εκφώνησή σου) πρέπει να δουλέψω με πλευρικά όρια ώστε να καταλήξω σε σχέση της μορφής
\leq 1/x \,\forall x>0 \kappa\alpha\iota\,g'(x) \geq 1/x \, \forall x>0)
που αυτό συνεπάγεται
=1/x \,\forall x>0)
. Σταθεροποιώ λοιπόν ένα
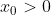
. Η f είναι παραγωγίσιμη στο
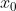
άρα και η g είναι παραγωγίσιμη στο
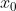
. Αυτό σημαίνει σύμφωνα με τον ορισμό της παραγώγου ότι
-g(x_0)}{x-x_0}=\lim_{x\to x_0^+}\frac{g(x)-g(x_0)}{x-x_0}=g'(x_0)\,\,(1))
Για
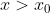
είναι
-g(x_0)}{x-x_0}\stackrel{x=x_0h,\,h>1}{=}\lim_{h\to 1^+}\frac{g(x_0h)-g(x_0)}{x_0(h-1)}\,(2))
Αυτό προκύπτει από το θεώρημα σχετικά με το όριο σύνθετης συνάρτησης(σελ. 173 σχολικό). Tώρα επειδή
=0)
, από την ανισότητα
\leq g(x_0)+g(h))
έχω
-g(x_0)\leq g(h) \Rightarrow \frac{g(x_0h)-g(x_0)}{x_0(h-1)} \leq \frac{g(h)}{x_0(h-1)} \Rightarrow \frac{g(x_0h)-g(x_0)}{x_0(h-1)} \leq \frac{g(h)-g(1)}{x_0(h-1))})
.
Από το θεώρημα 2 σελ. 166 σχολικού μπορώ σε αυτή την ανισότητα να περάσω όρια οπότε
-g(x_0)}{x_0(h-1)} \leq \lim_{h\to1^+}\frac{g(h)-g(1)}{x_0(h-1)}\,(3))
Όμως
-g(1)}{x_0(h-1)}=\frac{1}{x_0}\lim_{h\to1^+}\frac{g(h)-g(1)}{(h-1)}=\frac{1}{x_0}g'(1)=\frac{1}{x_0})
Άρα από τις σχέσεις (1),(2),(3) και την τελευταία έχω
 \leq \frac{1}{x_0})
. Εντελώς όμοια αποδεικνύεται και ότι
 \geq \frac{1}{x_0})
. To μόνο που αλλάζει είναι παίρνω αριστερά πλευρικά όρια(για
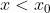
) κι ότι επειδή h<1 όταν διαιρώ την ανισότητα με h-1 αλλάζει η φορά και γίνεται
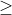
. Άρα για το τυχαίο
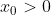
απέδειξα ότι
=\frac{1}{x_0})
. Αυτό σημαίνει ότι
=\frac{1}{x},\,\forall x>0)
. Από εδώ για κάθε χ>0 έχουμε
=\frac{1}{x} \Rightarrow g'(x)=(\ln x)' \Rightarrow g(x)= \ln x + c)
H τελευταία συνεπαγωγή προέκυψε από το πόρισμα σελ 251 σχολικού.
Επειδή
=0)
αντικαθιστώντας στην τελευταία σχέση χ=1 έχω
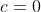
. Άρα τελικά
=\ln x \Rightarrow \frac{f(x)}{x}=\ln x \Rightarrow f(x)=x \ln x)
. Ένα τελευταίο βήμα είναι να επαληθεύσουμε ότι η συνάρτηση αυτή ικανοποιεί την αρχική ανισότητα για κάθε χ,y>0. Πράγματι
= xy (\ln x + \ln y ) = xy \ln x + xy \ln y )
. Τελειώσαμε!