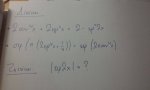manolis_98
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Guest 190013
Επισκέπτης
SnowLover
Νεοφερμένο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 9 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
αυγή όντος
Διάσημο μέλος


Μια άσκηση που έπεσε σήμερα σε ενδοσχολικές. Ιδέες κανείς;
κάνε fermat κάτω από τριγωνικό ραντάρ και μετά ψήσε σε προθερμασμενο φούρνο για δέκα λεπτά στους 200.
Σημείωση: Το μήνυμα αυτό γράφτηκε 9 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
lkjhgfdsa
Δραστήριο μέλος


Γράψε τη δεεύτερη σχέση σε μορφή λόγων ημιτόνων-συνημιτόνων.Μια άσκηση που έπεσε σήμερα σε ενδοσχολικές. Ιδέες κανείς;
Κάνε πολλαπλασιασμούς κατά μέλη, ώστε να φέρεις τα δύο "συν" πολλαπλασιαστικά μαζί (συνα*συνβ) και το ίδιο και για τα ημίτονα.
Φέρε τα όλα στο ένα μέλος μέ τέτοιο τρόπο ώστε τα δύο ημ να έχουν το πλην.
Χρησιμοποίησε τη σχέση συνημιτόνου αθροίσματος γωνιών.
Θα έρθεις σε μία μορφή συν[α+β]=0, τη λύνεις (κπ+π/2), χρησιμοποιείς και την ταυτότητα που σου δίνει στην αρχή, μετά το συν^2+ημ^2=1 και τελείωσες.
Αυτή η σχέση, βέβαια, δεν είναι γενική, ισχύει για τα χ που ικανοποιούν την εξίσωση που σου δίνει (τη 2η σχέση).
Σημείωση: Το μήνυμα αυτό γράφτηκε 9 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Guest 190013
Επισκέπτης


Υ.Γ. Είσαι μεγάλος

Σημείωση: Το μήνυμα αυτό γράφτηκε 9 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
ougka pougka
Εκκολαπτόμενο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 7 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Samael
Τιμώμενο Μέλος


Γιατι στην εξισωση 3lnx+2=0 η στην log(2x-1)+1=0 δεν παιρνουμε περιορισμους, ενω στην ln(x-2)-1=0 παιρνουμε?
Εαν θεωρησεις συναρτησεις πρεπει να παρεις περιορισμους.Στην πρωτη θες x>0 στην δευτερη x >1/2 ενω στην αλλη x>2.Εαν προκυψουν σαν εξισωσεις οπως παραπανω δεν ειναι αναγκη να μιλησεις για περιορισμους καθως οι λυσεις και φυσικα υπαρχουν,οποτε απλα λυνεις.
Εαν εχεις ομως ενα συστημα για παραδειγμα οπως αυτο :
ln(x-2)=1
x+3=0
Πρεπει x=-3 απο την δευτερη. Ομως τοτε x-2 = -3-2=-5 . Αλλα δεν οριζεται λογαριθμος αρνητικου αριθμου.
Επομενως δεν υπαρχει λυση του συστηματος.Εδω λοιπον χρειαστηκε να μιλησεις για περιορισμο.
Αλλα η 1η εξισωση εχει λυση x=e+2 και δεν χρειαζεται να παρεις περιορισμους εαν την εβλεπες σαν μεμονωμενη εξισωση.
Σημείωση: Το μήνυμα αυτό γράφτηκε 7 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
ougka pougka
Εκκολαπτόμενο μέλος


Πωπω καπως ετσι μπερδευομουν και στην τριγωνομετρια, ποτε θα πω κατευθειαν οτι το ημιτονο αυτης της γωνιας κανει τοσο και ποτε θα λυσω τριγωνομετρικη εξισωση

Σημείωση: Το μήνυμα αυτό γράφτηκε 7 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Samael
Τιμώμενο Μέλος


Μα και το ln(x-2)-1=0 μεμονωμενο ειναι..
Πωπω καπως ετσι μπερδευομουν και στην τριγωνομετρια, ποτε θα πω κατευθειαν οτι το ημιτονο αυτης της γωνιας κανει τοσο και ποτε θα λυσω τριγωνομετρικη εξισωση
Αυτο σου εξηγησα,οτι απο την στιγμη που ειναι μεμονωμενο δεν εχει τοοοση σημασια να μιλησεις για περιορισμους.Να στο πω αλλιως η f(x) = lnx οριζεται για x>0 αρα πεδιο ορισμου το Af = (0,+oo) και εχει συνολο τιμων f(A) = R .
Επομενως καθε εξισωση της μορφης lnx - c =0 η lnx = c θα εχει ΠΑΝΤΑ λυση εντος του πεδιου ορισμου αρα δεν χρειαζεται να μιλας για περιορισμο απλα λυνεις.Εαν θες το λες αλλα το θεωρω περιττο.
Εαν γενικευσουμε μια συναρτηση g(x) με συνολο τιμων το g(A) = (1,+oo) και πεδιο ορισμου Αg = R οταν γινει συνθεση με την f (μπει μεσα στην f που ειναι η lnx) θα ειναι η προηγουμενη εξισωση της μορφης :
ln(g(x)) = c .
Η εικονα της g ειναι το (1,+oo) αρα μεσα στο ln θα βρεθουν τιμες >1.
Εαν σου θεσω η σταθερα c = 0 . Τοτε εχεις την ln(g(x)) = 0 που βρισκεις οτι πρεπει g(x)=1.Κατι που δεν θα γινει ποτε αφου δεν ανηκει στο συνολο τιμων της.
Οπως και γενικα για οποιοδηποτε c<0 γιατι για να δωσει λογαριθμος αρνητικο αποτελεσμα πρεπει μεσα του να βρεθει αριθμος x τετοιος ωστε 0<x<1.
Στην περιπτωση της lnx = c το c μπορει να ειναι οτι θελει απο το πλην απειρο ως το συν απειρο διοτι σου δινω πεδιο ορισμου το (0,+οο) - σημειωση καθως το x πλησιαζει το 0 η lnx εκτοξευεται στο -οο στην γραφικη της παρασταση οποτε μην σου κανει εντυπωση. Στο +οο ειναι πιο διαισθητικα αντιληπτο οτι παει στο +οο.
Ελπιζω να κατανοεις λιγο τι λεω και να μην σε μπερδευω.Οτι δεν καταλαβαινεις πες μου.
Σημείωση: Το μήνυμα αυτό γράφτηκε 7 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Nia Skg
Εκκολαπτόμενο μέλος


Σε λίγες μέρες ξεκινάω την Β λυκείου και έχω αγχωθεί πάρα πολύ με το θέμα της άλγεβρας. Είμαι μαθήτρια του 3ου πεδίου που σημαίνει ότι θα δώσω βιολογία κι όχι μαθηματικά, γι'αυτό και θα πάω φροντιστήριο μόνο στα μαθήματα που με ενδιαφέρουν. Δεν υπάρχει δυνατότητα να κάνω ιδιαίτερα ή κάτι τέτοιο στα υπόλοιπα.. Τέλος πάντων, ο μαθηματικός που θα έχουμε στο σχολείο είναι αρκετά καλός (από όσο ξέρω) ωστόσο φοβάμαι ότι δεν θα καταφέρω να γράψω έναν καλό βαθμό στις εξετάσεις. Δε θέλω να χαλάσει ο μέσος όρος μου που σημαίνει ότι πρέπει να παίρνω 19-20 και χωρίς κάποια βοήθεια είναι σχεδόν ανέφικτο. Έχετε κάποιο καλό βοήθημα να μου προτείνετε για την άλγεβρα (γενικής); Κι αν ναι, ποιο; Ευχαριστώ εκ των προτέρων!!
Σημείωση: Το μήνυμα αυτό γράφτηκε 6 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Δημ.Μοσχόπουλος
Νεοφερμένο μέλος


Γεια σας ^^
Σε λίγες μέρες ξεκινάω την Β λυκείου και έχω αγχωθεί πάρα πολύ με το θέμα της άλγεβρας. Είμαι μαθήτρια του 3ου πεδίου που σημαίνει ότι θα δώσω βιολογία κι όχι μαθηματικά, γι'αυτό και θα πάω φροντιστήριο μόνο στα μαθήματα που με ενδιαφέρουν. Δεν υπάρχει δυνατότητα να κάνω ιδιαίτερα ή κάτι τέτοιο στα υπόλοιπα.. Τέλος πάντων, ο μαθηματικός που θα έχουμε στο σχολείο είναι αρκετά καλός (από όσο ξέρω) ωστόσο φοβάμαι ότι δεν θα καταφέρω να γράψω έναν καλό βαθμό στις εξετάσεις. Δε θέλω να χαλάσει ο μέσος όρος μου που σημαίνει ότι πρέπει να παίρνω 19-20 και χωρίς κάποια βοήθεια είναι σχεδόν ανέφικτο. Έχετε κάποιο καλό βοήθημα να μου προτείνετε για την άλγεβρα (γενικής); Κι αν ναι, ποιο; Ευχαριστώ εκ των προτέρων!!
Μην κοιτάτε μόνο το τι βαθμό θα πρέπει να γράφετε, αλλά το τι πρέπει να αποκομίσετε από την πλουσιότατη θεωρία της Άλγεβρας Β΄Λυκείου και για τις μετέπειτα σπουδές σας.
Ως προς το βοήθημα που ζητάτε δεν θα σας συστήσω κάποιο συγκεκριμένο και διαφωνώ με όποιον το κάνει. Λόγοι, δύο:
1ος
Αποτελεί άμεση διαφήμιση του βιβλίου που κάποιος θα προτείνει, αδικώντας άλλα εξίσου καλά ή και καλύτερα του προτεινόμενου.
2ος
Δεν ταιριάζουν όλα τα βοηθήματα σε όλους τους μαθητές.
Το καλύτερο που έχετε να κάνετε είναι να συμβουλευτείτε τον καθηγητή σας, στο σχολείο ή στο φροντιστήριο, που ξέρει την δυναμική σας. Αυτός/-ή θα σας προτείνει ένα βιβλίο κατάλληλο για σας.
Ελπίζω ο καθηγητής στο σχολείο σας να είναι όσο καλός σάς είπαν ότι είναι και, σε συνδυασμό με το βιβλίο που θα σας προτείνει, να έχετε καλή κατανόηση και δυνατότητα αντιμετώπισης βασικών θεμάτων Άλγεβρας.
Σημείωση: Το μήνυμα αυτό γράφτηκε 6 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Samael
Τιμώμενο Μέλος


Γεια σας ^^
Σε λίγες μέρες ξεκινάω την Β λυκείου και έχω αγχωθεί πάρα πολύ με το θέμα της άλγεβρας. Είμαι μαθήτρια του 3ου πεδίου που σημαίνει ότι θα δώσω βιολογία κι όχι μαθηματικά, γι'αυτό και θα πάω φροντιστήριο μόνο στα μαθήματα που με ενδιαφέρουν. Δεν υπάρχει δυνατότητα να κάνω ιδιαίτερα ή κάτι τέτοιο στα υπόλοιπα.. Τέλος πάντων, ο μαθηματικός που θα έχουμε στο σχολείο είναι αρκετά καλός (από όσο ξέρω) ωστόσο φοβάμαι ότι δεν θα καταφέρω να γράψω έναν καλό βαθμό στις εξετάσεις. Δε θέλω να χαλάσει ο μέσος όρος μου που σημαίνει ότι πρέπει να παίρνω 19-20 και χωρίς κάποια βοήθεια είναι σχεδόν ανέφικτο. Έχετε κάποιο καλό βοήθημα να μου προτείνετε για την άλγεβρα (γενικής); Κι αν ναι, ποιο; Ευχαριστώ εκ των προτέρων!!
Φιλικη συμβουλη. Ασε τα 20αρια για μ.ο. και δωσε βαση στα μαθηματα που θα πας για πανελληνιες. Μετα απο χρονια ουτε θα θυμασαι ουτε θα σε αφορα η διανυσματικη αλγεβρα. Με αυτο το σκεπτικο οποιοδηποτε γνωστο βοηθημα θα σε καλυψει με το παραπανω
Σημείωση: Το μήνυμα αυτό γράφτηκε 6 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Dimitris_Gr
Νεοφερμένο μέλος


Γεια σας ^^
Σε λίγες μέρες ξεκινάω την Β λυκείου και έχω αγχωθεί πάρα πολύ με το θέμα της άλγεβρας. Είμαι μαθήτρια του 3ου πεδίου που σημαίνει ότι θα δώσω βιολογία κι όχι μαθηματικά, γι'αυτό και θα πάω φροντιστήριο μόνο στα μαθήματα που με ενδιαφέρουν. Δεν υπάρχει δυνατότητα να κάνω ιδιαίτερα ή κάτι τέτοιο στα υπόλοιπα.. Τέλος πάντων, ο μαθηματικός που θα έχουμε στο σχολείο είναι αρκετά καλός (από όσο ξέρω) ωστόσο φοβάμαι ότι δεν θα καταφέρω να γράψω έναν καλό βαθμό στις εξετάσεις. Δε θέλω να χαλάσει ο μέσος όρος μου που σημαίνει ότι πρέπει να παίρνω 19-20 και χωρίς κάποια βοήθεια είναι σχεδόν ανέφικτο. Έχετε κάποιο καλό βοήθημα να μου προτείνετε για την άλγεβρα (γενικής); Κι αν ναι, ποιο; Ευχαριστώ εκ των προτέρων!!
WTF!? Για ποιο λόγο να φοβάσαι να χάσεις το μέσο όρο σου;
Σημασία έχουν μόνο οι πανελλαδικές και άντε λίγο το απολυτήριο που θα ασχοληθείς με αυτό του χρόνου.
Σημείωση: Το μήνυμα αυτό γράφτηκε 6 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Μάρκος Βασίλης
Πολύ δραστήριο μέλος


Φιλικη συμβουλη. Ασε τα 20αρια για μ.ο. και δωσε βαση στα μαθηματα που θα πας για πανελληνιες. Μετα απο χρονια ουτε θα θυμασαι ουτε θα σε αφορα η διανυσματικη αλγεβρα. Με αυτο το σκεπτικο οποιοδηποτε γνωστο βοηθημα θα σε καλυψει με το παραπανω
Σε σχέση με το μαρκαρισμένο, να πω ότι, εν πολλοίς, διαφωνώ. Ναι, δε χρειάζεται να κυνηγάμε βαθμούς κ.λπ., γιατί δεν είναι αυτή η ουσία της εκπαίδευσης, αλλά, αν μία μαθήτρια/ένας μαθητής θέλει να έχει έναν στόχο, δεν είναι κακό, εφ' όσον ο στόχος δε γίνεται αυτοσκοπός, να την/τον παροτρύνουμε να τον πετύχει. Αντ' αυτού, εγώ θα σε συμβούλευα (προς Nia Skg), να πάρεις, στο βαθμό που το πρόγραμμά σου και τα διαβάσματά σου στο επιτρέπουν, όσα περισσότερα μπορείς από τα μαθήματα γενικής παιδείας που θα δεις φέτος (ειδικότερα, και από την άλγεβρα). Άλλωστε, η γενική παιδεία είναι (ή θα έπρεπε να είναι, Ελλάδα γαρ) αυτό ακριβώς που λέει: «Γενική Παιδεία».
Μην αποκτήσεις, τουλάχιστον από φέτος, τη νοοτροπία του «δεν το δίνω, δε με νοιάζει», γιατί, πραγματικά, δε θα σε ωφελήσει στη ζωή σου, μακροπρόθεσμα. Αλλά, από την άλλη, όπως σωστά επισημαίνουν και ο κ. Μοσχόπουλος αλλά και ο Samael (ως προς αυτήν την κατεύθυνση), μη βρεθείς να «τρέχεις» πίσω από τους βαθμούς. Και 18 και 17 και 16 να έχεις λ.χ. στη λογοτεχνία, αν δεν είναι το «φόρτε» σου ή ο έρωτας της ζωής σου ή, εν πάσει περιπτώσει, σε δυσκολεύει, δε χάλασε κι ο κόσμος!
Πίσω στην άλγεβρα, το καλύτερο που έχεις να κάνεις είναι, και κατ' εμέ, να εξηγήσεις την κατάσταση στον καθηγητή σου και να ζητήσεις και τη δική του συμβουλή.
Ό,τι κι αν κάνεις, καλή τύχη φέτος!
Σημείωση: Το μήνυμα αυτό γράφτηκε 6 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Samael
Τιμώμενο Μέλος


Δεν ανέφερε καν να ανησυχεί για το πως θα καταλαβαίνει φυσική του χρόνου που θα την δίνει εαν δεν τα πάει καλά στην διανυσματική άλγεβρα της Β λυκείου . Επομένως σε εμένα το θέλω να βγάλω 20 μου ακούγεται αυτοσκοπόςΣε σχέση με το μαρκαρισμένο, να πω ότι, εν πολλοίς, διαφωνώ. Ναι, δε χρειάζεται να κυνηγάμε βαθμούς κ.λπ., γιατί δεν είναι αυτή η ουσία της εκπαίδευσης, αλλά, αν μία μαθήτρια/ένας μαθητής θέλει να έχει έναν στόχο, δεν είναι κακό, εφ' όσον ο στόχος δε γίνεται αυτοσκοπός, να την/τον παροτρύνουμε να τον πετύχει. Αντ' αυτού, εγώ θα σε συμβούλευα (προς Nia Skg), να πάρεις, στο βαθμό που το πρόγραμμά σου και τα διαβάσματά σου στο επιτρέπουν, όσα περισσότερα μπορείς από τα μαθήματα γενικής παιδείας που θα δεις φέτος (ειδικότερα, και από την άλγεβρα). Άλλωστε, η γενική παιδεία είναι (ή θα έπρεπε να είναι, Ελλάδα γαρ) αυτό ακριβώς που λέει: «Γενική Παιδεία».
Μην αποκτήσεις, τουλάχιστον από φέτος, τη νοοτροπία του «δεν το δίνω, δε με νοιάζει», γιατί, πραγματικά, δε θα σε ωφελήσει στη ζωή σου, μακροπρόθεσμα. Αλλά, από την άλλη, όπως σωστά επισημαίνουν και ο κ. Μοσχόπουλος αλλά και ο Samael (ως προς αυτήν την κατεύθυνση), μη βρεθείς να «τρέχεις» πίσω από τους βαθμούς. Και 18 και 17 και 16 να έχεις λ.χ. στη λογοτεχνία, αν δεν είναι το «φόρτε» σου ή ο έρωτας της ζωής σου ή, εν πάσει περιπτώσει, σε δυσκολεύει, δε χάλασε κι ο κόσμος!
Πίσω στην άλγεβρα, το καλύτερο που έχεις να κάνεις είναι, και κατ' εμέ, να εξηγήσεις την κατάσταση στον καθηγητή σου και να ζητήσεις και τη δική του συμβουλή.
Ό,τι κι αν κάνεις, καλή τύχη φέτος!
 .
.Σε κάθε περίπτωση σημασία δεν έχει να μπορεί να λύσει κάθε hardcore άσκηση που θα βρει σε κάποιο βοήθημα ή να γράψει 20 στο τέλος αλλά να αντιληφθεί τις ιδέες που διέπουν τα ευκλείδεια διανύσματα . Στην πράξη δεν θα χρειαστεί κάτι παραπάνω απο πρόσθεση και αφαίρεση διανυσμάτων και άντε με το ζόρι κανένα εσωτερικό γινόμενο(που δεν...εδώ δεν ήξεραν το εμβαδόν του κύκλου) . Αντίθετα πρέπει να κατανοεί πλήρως τις έννοιες του μέτρου & της κατεύθυνσης .
Σημείωση: Το μήνυμα αυτό γράφτηκε 6 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Nia Skg
Εκκολαπτόμενο μέλος


Δεν ανέφερε καν να ανησυχεί για το πως θα καταλαβαίνει φυσική του χρόνου που θα την δίνει εαν δεν τα πάει καλά στην διανυσματική άλγεβρα της Β λυκείου . Επομένως σε εμένα το θέλω να βγάλω 20 μου ακούγεται αυτοσκοπός.
Σε κάθε περίπτωση σημασία δεν έχει να μπορεί να λύσει κάθε hardcore άσκηση που θα βρει σε κάποιο βοήθημα ή να γράψει 20 στο τέλος αλλά να αντιληφθεί τις ιδέες που διέπουν τα ευκλείδεια διανύσματα . Στην πράξη δεν θα χρειαστεί κάτι παραπάνω απο πρόσθεση και αφαίρεση διανυσμάτων και άντε με το ζόρι κανένα εσωτερικό γινόμενο(που δεν...εδώ δεν ήξεραν το εμβαδόν του κύκλου) . Αντίθετα πρέπει να κατανοεί πλήρως τις έννοιες του μέτρου & της κατεύθυνσης .
Παιδιά, ο μέσος όρος με προβληματίζει καθαρά επειδή έχω αυστηρό πατέρα και δεν δέχεται βαθμούς κάτω του 19 (δεν κάνω πλάκα). Εμένα φυσικά και με ενδιαφέρουν περισσότερο οι γνώσεις που θα αποκτήσω στην άλγεβρα κι όχι ένας αριθμός στο χαρτί με τους ελέγχους. Ευχαριστώ πάντως!
Σημείωση: Το μήνυμα αυτό γράφτηκε 6 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Samael
Τιμώμενο Μέλος


Παιδιά, ο μέσος όρος με προβληματίζει καθαρά επειδή έχω αυστηρό πατέρα και δεν δέχεται βαθμούς κάτω του 19 (δεν κάνω πλάκα). Εμένα φυσικά και με ενδιαφέρουν περισσότερο οι γνώσεις που θα αποκτήσω στην άλγεβρα κι όχι ένας αριθμός στο χαρτί με τους ελέγχους. Ευχαριστώ πάντως!
Δεν είμαι ακριβώς σίγουρος για το τι πρέπει να σου πω τώρα . Πες στον πατέρα σου απλά να συνειδητοποιήσει τι συμβαίνει έξω στον κόσμο, με τρόπο
 . Δεν χρειάζεσαι το απόλυτο 20 ούτε το 17 ή το 16 είναι ντροπής βαθμός .
. Δεν χρειάζεσαι το απόλυτο 20 ούτε το 17 ή το 16 είναι ντροπής βαθμός .Σημείωση: Το μήνυμα αυτό γράφτηκε 6 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Μάρκος Βασίλης
Πολύ δραστήριο μέλος


Δεν ανέφερε καν να ανησυχεί για το πως θα καταλαβαίνει φυσική του χρόνου που θα την δίνει εαν δεν τα πάει καλά στην διανυσματική άλγεβρα της Β λυκείου . Επομένως σε εμένα το θέλω να βγάλω 20 μου ακούγεται αυτοσκοπός.
Σε κάθε περίπτωση σημασία δεν έχει να μπορεί να λύσει κάθε hardcore άσκηση που θα βρει σε κάποιο βοήθημα ή να γράψει 20 στο τέλος αλλά να αντιληφθεί τις ιδέες που διέπουν τα ευκλείδεια διανύσματα . Στην πράξη δεν θα χρειαστεί κάτι παραπάνω απο πρόσθεση και αφαίρεση διανυσμάτων και άντε με το ζόρι κανένα εσωτερικό γινόμενο(που δεν...εδώ δεν ήξεραν το εμβαδόν του κύκλου) . Αντίθετα πρέπει να κατανοεί πλήρως τις έννοιες του μέτρου & της κατεύθυνσης .
Κοίτα, ως μαθηματικός οφείλω να πω ότι δεν έχει νόημα να μαθαίνεις τα μαθηματικά που θα δεις στην «πράξη». Εξηγούμαι. Στην πράξη, αν αυτή είναι η καθημερινή ζωή, αρκούν οι τρεις πράξεις και, επί της ουσίας, μεταξύ ρητών. Στην πράξη, αν αυτή είναι η καθημερινότητα ενός βιολόγου, του αρκεί να χειρίζεται το SPSS. Δεν είναι όμως αυτός ο λόγος που βάλαμε τα παιδιά να ταλαιπωρούνται επί 2 και κάτι χιλιετίες για 12 χρόνια της ζωής τους με τα μαθηματικά.
Για παράδειγμα, η παρεξηγημένη κατεύθυνση της Β' λυκείου έχει έναν πολύ βαθύτερο σκοπό (που συνήθως πάει άκλαφτος). Παίρνει ένα αντικείμενο που ο μαθητής το έβλεπε υπό μία δεδομένη μορφή (την Ευκλείδεια Γεωμετρία) και του αλλάζει τα φώτα. Από εκεί που μία άσκηση γεωμετρίας ήταν ένα σχήμα και μία παράγραφος με επιχειρήματα (γυμναστική στην προτασιακή λογική - γι' αυτό είναι η γεωμετρία στο αναλυτικό πρόγραμμα, όχι για να μετρήσω το χωράφι του παππού μου) τώρα γίνεται ένα σύστημα εξισώσεων. Δηλαδή, αλγεβροποιεί το Ευκλείδειο επίπεδο, παρέχοντάς μας ένα μοντέλο των αξιωμάτων της Ευκλείδειας Γεωμετρίας (το R^2). Στην ουσία, αυτή η διαδικασία της μοντελοποίησης είναι που πρέπει κανείς να τονίζει σε όλη τη διάρκεια της Β' λυκείου (σε ό,τι έχει να κάνει με τα μαθηματικά κατεύθυνσης). Το πώς, δηλαδή, στην προκειμένη, κάτι εν γένει δύσκολο και δύσχρηστο (την κλασσική γεωμετρία) την ανάγουμε σε κάτι που χειριζόμαστε πιο εύκολα (την άλγεβρα).
Με λίγα λόγια, όλη η ύλη της κατεύθυνσης της Β' είναι η κατασκευή ενός μοντέλου της Ευκλείδειας Γεωμετρίας. Αυτό όμως δεν κάνει κανείς και στα τρία χρόνια Φυσικής του λυκείου; Ιδανικές συνθήκες, αγνοούμε τριβές και, γενικά, κατασκευάζουμε ένα μαθηματικό μοντέλο του φυσικού κόσμου. Προφανώς και δεν είναι η ίδια διαδικασία, καθώς στη φυσική υπεισέρχεται η έννοια της προσέγγισης, αλλά η ιδέα της μοντελοποίησης μιας κατάστασης μέσω μιας άλλης γνωστής κατάστασης είναι αυτή που εμφανίζεται και στα δύο.
Κλείνοντας την επιστημολογική παρένθεση και για να γυρίσουμε και στο θέμα μας, Nia Skg, μπορείς, όπως σε συμβούλεψε κι ο Samael, να εξηγήσεις στον πατέρα σου πώς έχει η κατάσταση και τα συναφή. Μια ιδέα θα ήταν, για παράδειγμα, να ζητήσεις και τη στήριξη ενός ατόμου (π.χ. καθηγητή; ) που εμπιστεύεσαι και νιώθεις ότι σε καταλαβαίνει, για να αισθανθείς κι εσύ πιο ασφαλής! Όπως και να έχει, καλή σχολική χρονιά!

Σημείωση: Το μήνυμα αυτό γράφτηκε 6 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Samael
Τιμώμενο Μέλος


Κοίτα, ως μαθηματικός οφείλω να πω ότι δεν έχει νόημα να μαθαίνεις τα μαθηματικά που θα δεις στην «πράξη». Εξηγούμαι. Στην πράξη, αν αυτή είναι η καθημερινή ζωή, αρκούν οι τρεις πράξεις και, επί της ουσίας, μεταξύ ρητών. Στην πράξη, αν αυτή είναι η καθημερινότητα ενός βιολόγου, του αρκεί να χειρίζεται το SPSS. Δεν είναι όμως αυτός ο λόγος που βάλαμε τα παιδιά να ταλαιπωρούνται επί 2 και κάτι χιλιετίες για 12 χρόνια της ζωής τους με τα μαθηματικά.
Για παράδειγμα, η παρεξηγημένη κατεύθυνση της Β' λυκείου έχει έναν πολύ βαθύτερο σκοπό (που συνήθως πάει άκλαφτος). Παίρνει ένα αντικείμενο που ο μαθητής το έβλεπε υπό μία δεδομένη μορφή (την Ευκλείδεια Γεωμετρία) και του αλλάζει τα φώτα. Από εκεί που μία άσκηση γεωμετρίας ήταν ένα σχήμα και μία παράγραφος με επιχειρήματα (γυμναστική στην προτασιακή λογική - γι' αυτό είναι η γεωμετρία στο αναλυτικό πρόγραμμα, όχι για να μετρήσω το χωράφι του παππού μου) τώρα γίνεται ένα σύστημα εξισώσεων. Δηλαδή, αλγεβροποιεί το Ευκλείδειο επίπεδο, παρέχοντάς μας ένα μοντέλο των αξιωμάτων της Ευκλείδειας Γεωμετρίας (το R^2). Στην ουσία, αυτή η διαδικασία της μοντελοποίησης είναι που πρέπει κανείς να τονίζει σε όλη τη διάρκεια της Β' λυκείου (σε ό,τι έχει να κάνει με τα μαθηματικά κατεύθυνσης). Το πώς, δηλαδή, στην προκειμένη, κάτι εν γένει δύσκολο και δύσχρηστο (την κλασσική γεωμετρία) την ανάγουμε σε κάτι που χειριζόμαστε πιο εύκολα (την άλγεβρα).
Με λίγα λόγια, όλη η ύλη της κατεύθυνσης της Β' είναι η κατασκευή ενός μοντέλου της Ευκλείδειας Γεωμετρίας. Αυτό όμως δεν κάνει κανείς και στα τρία χρόνια Φυσικής του λυκείου; Ιδανικές συνθήκες, αγνοούμε τριβές και, γενικά, κατασκευάζουμε ένα μαθηματικό μοντέλο του φυσικού κόσμου. Προφανώς και δεν είναι η ίδια διαδικασία, καθώς στη φυσική υπεισέρχεται η έννοια της προσέγγισης, αλλά η ιδέα της μοντελοποίησης μιας κατάστασης μέσω μιας άλλης γνωστής κατάστασης είναι αυτή που εμφανίζεται και στα δύο.
Κλείνοντας την επιστημολογική παρένθεση και για να γυρίσουμε και στο θέμα μας, Nia Skg, μπορείς, όπως σε συμβούλεψε κι ο Samael, να εξηγήσεις στον πατέρα σου πώς έχει η κατάσταση και τα συναφή. Μια ιδέα θα ήταν, για παράδειγμα, να ζητήσεις και τη στήριξη ενός ατόμου (π.χ. καθηγητή; ) που εμπιστεύεσαι και νιώθεις ότι σε καταλαβαίνει, για να αισθανθείς κι εσύ πιο ασφαλής! Όπως και να έχει, καλή σχολική χρονιά!
Τα μαθηματικά που θα δει κάποιος στην πράξη δεν έχουν λιγότερη αξία απο αυτά που θα δει σε ένα πιο καθαρό μάθημα μαθηματικών . Μάλιστα ίσα ίσα που στην σημερινή εποχή λόγω του τεράστιου όγκου της ύλης,δεν γίνεται να μάθει κανείς τα πάντα,και το να αναλώνεται σε όλες τις μαθηματικές λεπτομέρειες απλά για να βγάλει απο 19 και πάνω σπανίως προσθέτει παραπάνω ουσία . Γι'αυτό και εμμένω στο οτι δεν θα υπάρξουν τραγικές συνέπειες εαν δεν πάρει 19, όχι τίποτα άλλο .
Καταλαβαίνω τι λέτε και δεν διαφωνώ καθόλου για την σημασία της διανυσματικής άλγεβρας, είναι αδιαμφισβήτητα εφόδιο σε κάθε μαθητή και μετέπειτα φοιτητή και επιστήμονα των θετικών σπουδών. Αλλά, όπως είπα ο χρόνος είναι περιορισμένος και ούτως η άλλως ελάχιστα παιδιά αντιλαμβάνονται τα όσα τονίσατε,πολύ όμορφα και κομψά μάλιστα . Ούτε πρόκειται απο ένα μάθημα που έτυχε να πάρουν στα 16-17 να αντιληφθούν όσα εσείς, μετά απο τόσα μαθήματα που έχετε πάρει σε διαφορετικούς τομείς και έχετε πλήρη εικόνα απο τις "ρίζες" αυτού του πολύ ωραίου και χρήσιμου κλάδου που επεκτείνονται και σε άλλους .
Ιδιαίτερα δε στην βιολογία κάτι παραπάνω απο τις βασικές πράξεις δεν έχω δει να χρησιμοποιούν . Στην χημεία ομοίως,λογάριθμους απο καθαρά υπολογιστική σκοπιά και λύση πρωτοβάθμιων και δευτεροβάθμιων εξισώσεων .Μαθήματα απο την άλλη όπως η στατιστική σε μια dumbed down έκδοση χωρίς λογισμό,φαίνονται εξαιρετικά χρήσιμα σε αυτά τα τμήματα . Δεν νομίζω οτι διαφωνούμε επι της ουσίας πάρα αυτά .Το νόημα μας είναι κοινό : εφόσον έχει θέμα και δυσκολεύεται δεν πρέπει να αγχώνεται και να πιέζεται να βγάλει άριστα σε ένα μάθημα που ούτως ή άλλως δεν θα χρειαστεί ποτέ της ή θα δεί καλύτερα στο πανεπιστήμιο στην χειρότερη . Επειδή όμως θα το χρειαστεί σίγουρα για να αντιληφθεί καλύτερα την φυσική του χρόνου,εννοείται οτι δεν πρέπει να το αφήσει και στο έλεος του Θεου ,εφόσον δεν της είναι παντελώς άσχετο με το εγγύτερο μέλλον .
Εξαίρεση στην εξής περίπτωση,εαν στοχεύει και σε χημικά,τότε κατα την γνώμη μου πρέπει οπωσδήποτε να δώσει βάση και να μην κάνει κενά χωρίς πάλι να σφαχτεί να βγάλει ντε και καλά άριστα γιατί είναι πολύ βασικές γνώσεις για να καταλάβει όταν με το καλό είναι φοιτήτρια, θέματα όπως η κρυσταλλογραφία . Βέβαια θα τα ακούσει ξανά αργότερα,αλλά γιατί να μην έχει μια ιδέα ήδη απο πριν
 .
.Σημείωση: Το μήνυμα αυτό γράφτηκε 6 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 1 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 46 μέλη διάβασαν αυτό το θέμα:
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki