Όπως ειπώθηκε και παραπάνω, το σύμβολο της συνεπαγωγής
)
σημαίνει στην ουσία ΑΝ ισχύει ό,τι είναι αριστερά του ΤΟΤΕ ΥΠΟΧΡΕΩΤΙΚΑ θα ισχύει και ό,τι είναι δεξιά του. Στην περίπτωση που ισχύει και η αντίστροφη πορεία της συνεπαγωγής και μόνο τότε χρησιμοποιείται το σύμβολο της ισοδυναμίας
)
, το οποίο στην ουσία σημαίνει ότι η πρόταση δεξιά του συμβόλου ισχύει ΑΝ ΚΑΙ ΜΟΝΟ ΑΝ ισχύει η πρόταση αριστερά του συμβόλου (ικανή και αναγκαία συνθήκη).
Η αλήθεια είναι ότι όποιος θέλει να γράφει σωστά μαθηματικά πρέπει να είναι πολύ προσεκτικός με αυτά τα σύμβολα. Για παράδειγμα θα ήταν μεγάλο λάθος να γράψει κάποιος
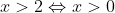
και αυτό γιατί
δεν ισχύει απαραίτητα ότι
αν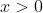 
τότε υποχρεωτικά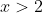 
. Ωστόσο δεν υπάρχει λογικό σφάλμα με το να γράψει ότι
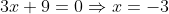
έστω και αν είναι ισοδύναμες εκφράσεις.
Είναι προφανές, λοιπόν, ότι η ισοδυναμία είναι πιο απαιτητική από την απλή συνεπαγωγή.
Κάπου εδώ μπαίνει και ο σκοπός των όσων γράφουμε. Αν κάποιος ζητάει να βρεθούν οι ρίζες της εξίσωσης
, ή η τιμή της συνάρτησης
=sin(\pi \sqrt{2}\cos(x)) )
στο
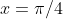
εμείς δεν είμαστε υποχρεωμένοι να του πούμε ποιες από τις εκφράσεις που θα γράψουμε είναι ισοδύναμες μεταξύ τους. Δεν χρειάζεται να «γυρίζει προς τα πίσω» η διαδικασία όπως λέμε απλοϊκά. Αρκεί να είναι σωστά τα προς τα εμπρός βήματα.
Από την άλλη μεριά, όταν χρησιμοποιούμε ή αποδεικνύουμε προτάσεις και θεωρήματα, τις περισσότερες φορές είναι ζήτημα ορθότητας η έννοια της ισοδυναμίας και της συνεπαγωγής. Για παράδειγμα, στο θεώρημα του Bolzano, ο άνθρωπος είπε ξεκάθαρα ότι ΑΝ οι τιμές μιας συνεχούς συνάρτησης στα άκρα ενός διαστήματος είναι ετερόσημες και μη μηδενικές ΤΟΤΕ ΥΠΟΧΡΕΩΤΙΚΑ η συνάρτηση αυτή έχει τουλάχιστον μία ρίζα στο διάστημα αυτό. Αν κάποιος βάλει ισοδυναμία εκεί είναι σαν λαμβάνει υπόψη του λάθος θεώρημα!
Η δική μου συμβουλή είναι αντί να γράφει κανείς, σύμβολα που δεν είναι βέβαιος αν είναι σωστά, να γράφει με λέξεις αυτό που θέλει να πει. Είναι ίσως το πλέον αποδεκτό από τους καθηγητές-διορθωτές. Μάλιστα, κατά τη γνώμη μου, βελτιώνει αρκετά και την εικόνα του γραπτού.
Δηλαδή για μια συνεπαγωγή ή ισοδυναμία μπορούμε να γράψουμε τη λέξη "έπεται" ή "επομένως", ενώ για πιο πολλές εκφράσεις μπορεί να χρησιμοποιηθεί στην αρχή η φράση "Έχουμε διαδοχικά:" και να γράψουμε τις εκφράσεις τη μία κάτω από την άλλη χωρίς σύμβολα συνεπαγωγής ή ισοδυναμίας. (Το διαζευκτικό "ή" δεν το προτείνω γιατί προσωπικά μου θυμίζει υπερβολικά την λογική διάζευξη (ή το Α ή το Β, ή και τα δύο), αλλά δεν παύει να είναι κι αυτό μια εν γένει αποδεκτή επιλογή.)
Δείγμα γραφής:
(1)
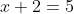έπεται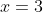 
.
(2)
Έχουμε διαδοχικά:
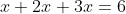
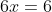
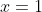
(3) Είναι
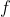
συνεχής στο
,
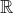
=1 )
και
=-5 )
.
Επομένως από θεώρημα Bolzano υπάρχει τουλάχιστον μία ρίζα στο διάστημα
 )
.
Τέλος θέλω να τονίσω ότι αυτά είναι λεπτομέρειες. Ίσως είναι το τελευταίο που πρέπει να σας αγχώνει/προβληματίζει ως μαθητές. Αν έχετε γράψει τις λύσεις κομψά θα είναι ακραίο να σας κόψουν έστω και 1% για αυτό το λόγο.
Sorry for the long post.
