Θεμα απο Ρουμανικο Διαγωνισμο
Κατι μου θυμιζει...εσας;
Έστω f συνεχής συνάρτηση στο [0,1] με
.Να αποδείξετε ότι:
α) Η συνάρτηση
που είναι ορισμένη στο [0,1] με
για x
διάφορο του μηδενός και
πληρεί τις προϋποθέσεις του θεωρήματος
Rolle στο [0 , 1]
β) Υπάρχει
τέτοιο , ώστε :
α) Η f είναι συνεχής στο [0,1], οπότε η συνάρτηση
=\int_{0}^{x}f(t)dt)
είναι παραγωγίσιμη στο [0,1] και ισχύει F'(x)=F(x) για κάθε
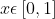
Η f είναι συνεχής στο [0,1], οπότε η συνάρτηση g(x)=xf(x) είναι συνεχής στο [0,1] και επομένως η συνάρτηση
=\int_{0}^{x}g(t)dt=\int_{0}^{x}tf(t)dt)
είναι παραγωγίσιμη στο [0,1] και ισχύει
=g(x)=xf(x))
για κάθε
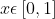
.
Η συνάρτηση
=\frac{G(x)}{x})
είναι παραγωγίσιμη στο (0,1] ως γινόμενο παραγωγίσιμων στο (0,1] συναρτήσεων και ισχύει
=\frac{xG'(x)-G(x)}{{x}^{2}}=\frac{{x}^{2}f(x)-G(x)}{{x}^{2}}=f(x)-\frac{G(x)}{{x}^{2}}=F'(x)-\frac{G(x)}{{x}^{2}})
Συνεπώς η συνάρτηση H απόκτά την μορφή
=\Phi (x)-F(x))
για κάθε

και επομένως είναι παραγωγίσιμη στο (0,1] με παράγωγο:
=\Phi' (x)-F'(x)=-\frac{G(x)}{{x}^{2}})
για κάθε

.
Οι συναρτήσεις F και G είναι συνεχείς στο [0,1] αφού είναι παραγωγίσιμες στο [0,1]. Συνεπώς είναι παραγωγίσιμες και συνεχείς στο 0 (από δεξιά).
=F(0)=\int_{0}^{0}f(t)dt=0)
=\int_{0}^{0}tf(t)dt=0)
=0f(0)=0)
-G(0)}{x-0}=G'(0)\Rightarrow \lim_{x\rightarrow {0}^{+}}\frac{G(x)}{x}=0)
=\lim_{x\rightarrow {0}^{+}}\frac{G(x)}{x}=0)
Έχουμε:
=\lim_{x\rightarrow {0}^{+}}\Phi (x)-\lim_{x\rightarrow {0}^{+}}F(x)=0-0=0=H(0))
Άρα η H είναι συνεχής (από δεξιά) στο 0
Η H είναι συνεχής στο (0,1] και ισχύει
=H(0))
, συνεπώς η H είναι συνεχής στο [0,1]
=\int_{0}^{1}tf(t)dt-\int_{0}^{1}f(t)dt=\int_{0}^{1}\left( tf(t)-f(t)\right)dt=\int_{0}^{1}(t-1)f(t)dt=\int_{0}^{1}(x-1)f(x)dx=0=H(0))
Η H είναι συνεχής στο [0,1], παραγωγίσιμη στο (0,1) και ισχύει H(0)=H(1). Άρα η H ικανοποιεί τις προϋποθέσεις του θεωρήματος Rolle στο διάστημα [0,1].
β) Σύμφωνα με το θεώρημα Rolle, υπάρχει τουλάχιστον ένα
)
τέτοιο ώστε
=0\Rightarrow -\frac{G(\xi )}{{\xi }^{2}}=0\Rightarrow G(\xi )=0)
Θεωρώ την συνάρτηση h με τύπο
=G(x){e}^{-x})
. Η συνάρτηση h είναι παραγωγίσιμη στο [0,1] ως γινόμενο παραγωγίσιμων συναρτήσεων στο [0,1] και ισχύει
=\left( G'(x)-G(x)\right){e}^{-x})
για κάθε

. Άρα η h είναι συνεχής στο [0,1] και παραγωγίσιμη στο (0,1).
=G(0){e}^{-0}=0)
=G(\xi ){e}^{-\xi }=0)
Συνεπώς
=h(\xi )=0)
Η h είναι συνεχής στο [0,ξ], παραγωγίσιμη στο (0,ξ) και ισχύει h(0)=h(ξ). Επομένως σύμφωνα με το θεώρημα Rolle υπάρχει τουλάχιστον ένα
)
τέτοιο ώστε:
=0\Rightarrow \left(G'(\alpha )-G(\alpha ) \right){e}^{-\alpha }=0\Rightarrow G(\alpha )=G'(\alpha )\Rightarrow \int_{0}^{\alpha }tf(t)dt=\alpha f(\alpha )\Rightarrow \int_{0}^{\alpha }xf(x)dx=\alpha f(\alpha ))
αφού το σύμβολο της σταθεράς ολοκλήρωσης δεν παίζει κανένα ρόλο.
Άρα υπάρχει τουλάχιστον ένα
)
εφοσον
)
τέτοιο ώστε
dx=\alpha f(\alpha ))
-----------------------------------------
Παραθέτω μία άσκηση η οποία ήταν σήμερα ένα πολύ καλό θεματάκι στο Πανεπιστήμιο Πειραιά.
Να υπολογισθεί το ολοκλήρωμα

.
Θεωρώ την συνάρτηση
=\frac{1}{{x}^{2}-8x+15}=\frac{1}{(x-3)(x-5)})
. Το πεδίο ορισμού της συνάρτησης είναι το
\bigcup \left(3,5 \right)\bigcup (5,+\propto ))
και είναι συνεχής στο Α ως ρητή. Άρα η f είναι συνεχής σε κάθε διάστημα
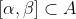
και επομένως ολοκληρώσιμη στο διάστημα αυτό. Θα υπολογιστεί το αόριστο ολοκλήρωμα της f στο [α,β]:
dx=\int \frac{dx}{{x}^{2}-8x+15}=\int \frac{dx}{(x-3)(x-5)}=\frac{1}{2}\int \frac{(x-3)-(x-5)}{(x-3)(x-5)}dx=\frac{1}{2}\int \frac{dx}{x-5}+\frac{1}{2}\int \frac{dx}{x-3}=\frac{1}{2}ln\left|x-5 \right|+\frac{1}{2}ln\left|x-3 \right|+c=\frac{1}{2}ln\left|\frac{x-5}{x-3} \right|+c)
όπου
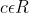
Θεωρώ την συνάρτηση
=\int_{7}^{t}f(x)dx)
η οποία είναι παραγωγίσιμη σε κάθε διάστημα
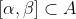
τέτοιο ώστε
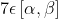
. Έχουμε
=\int_{7}^{t}\frac{dx}{{x}^{2}-8x+15}=\frac{1}{2}\left(ln\left|\frac{t-5}{t-3}\right|-ln\left|\frac{2}{4} \right| \right)=\frac{1}{2}ln\left|\frac{2t-10}{t-3}\right|)
.
Η F είναι παραγωγίσιμη στο διάστημα
)
καθώς η f είναι συνεχής σε αυτό και ισχύει F'(t)=f(t) για κάθε
)
Είναι
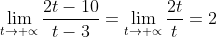
Θέτω
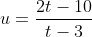
. Έχουμε
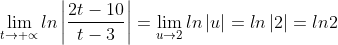
Άρα
=\frac{ln2}{2})
. Συνεπώς υπάρχει το γενικευμένο ολοκλήρωμα και ισχύει
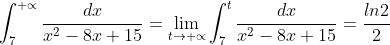
.