εγώ όταν είχα ρωτήσει μου χαν πει πρέπει με κάποιον τρόπο να εμφανίσεις το f(Xo)
πχ εδώ το όριο αν το σπάγαμε σε
=0)
( το δεύτερο όριο κάνει f(0) λόγω συνέχειας από το πρώτο ερώτημα). Τώρα βέβαια κι αυτό δεν ξέρω αν είναι απόλυτα σωστό.
Ωπ, φάουλ. Μπορεί και να είσαι σωστός,
αλλά δεν σπάμε ΠΟΤΕ όρια εάν δεν έχουμε πρώτα βεβαιωθεί ότι υπάρχουν και είναι πραγματικά!
Που σημαίνει ότι είναι "λάθος" να γράψεις εξ' αρχής:
=\frac{1}{2}\lim_{x\rightarrow 0}x\cdot\lim_{x\rightarrow 0}x\ln{x}=\ldots)
Θα πρέπει πρώτα να γράψεις ότι:
=f(0)\in\mathbb{R})
, λόγω συνέχειας
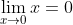
Και μετά λες ότι επειδή τα επιμέρους όρια
υπάρχουν και είναι πραγματικά τότε λες και ότι:
=\frac{1}{2}\lim_{x\rightarrow 0}x\cdot\lim_{x\rightarrow 0}x\ln{x}=\frac{1}{2}\cdot 0 \cdot f(0)=0)
-----------
Χαρακτηριστικό αντι-παράδειγμα είναι το:
=0)
Το οποίο υπάρχει και είναι και πραγματικό και ίσο με μηδέν. Όμως ΔΕΝ μπορείς να τα σπάσεις, γιατί το ...
=0)
ΔΕΝ ΥΠΑΡΧΕΙ καν! Πρόσεξε, δεν είναι ούτε μηδέν, ούτε άπειρο. ΔΕΝ υπάρχει.
Η συνάρτηση αυτή κοντά στο μηδέν, μουρλαίνεται απίστευτα και ταλαντώνεται πάνω-κάτω μεταξύ των +/- 1 με αποτέλεσμα να μην "στέκεται" κάπου.
Εάν πας και το σπάσεις και πεις "ωραία, είναι μηδέν επί κάτι άλλο, άρα μηδέν" θα σε πάρουν με τις πέτρες. Γιατί αυτό το "κάτι άλλο" δεν υπάρχει καν...
Αν σου δώσει ο άλλος Σ-Λ που να λέει.
" Η συνάρτηση f(x)=1/x , δεν είναι συνεχής στο μηδέν."
Εδώ τι είναι; γιατί από τη μία συνεχής δεν είναι, αλλά από την άλλη δεν ορίζεται καν για να μιλάμε για συνέχεια.
Η πρόταση αυτή δεν είναι ούτε Σωστή, ούτε Λάθος, συνεπώς δεν θα στο δώσει. Να είσαι 100% σίγουρος.
Είναι σαν να σε ρωτάει ότι "Ισχύει 3/0 = 0", που δεν είναι ούτε σωστό, ούτε λάθος. Δεν έχει καν νόημα!
Μην αγχώνεσαι για τέτοια πράγματα. Αν 1 στις 100 το βάλουν, ζήτα εκείνη την ώρα διευκρίνιση και προσπέρνα το. Εάν είναι έξυπνοι, θα ακυρώσουν επί τόπου το ερώτημα. Αλλιώς ... κάνε ό,τι καταλαβαίνεις.
Αλλά είπαμε, τόσο μουρλοί δεν είναι, οπότε μην αγχώνεστε.