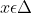Επειδή η f είναι κοίλη (και παραγωγίσιμη) στο R, τότε η πρώτη παράγωγος f' είανι γνησίως φθίνουσα στο R που σημαίνει ότι για κάθε
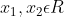
με
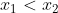
ισχύει
>f\left( {x}_{2}\right))
>f'\left( {x}_{0}\right))
<f'\left( {x}_{0}\right))
Άρα
>f'\left( {x}_{0}\right))
για κάθε
)
και
<f'\left( {x}_{0}\right))
για κάθε
)
όπου
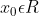
Θεωρώ την συνάρτηση
=f(x)-xf'\left( {x}_{0}\right)-f\left({x}_{0} \right)+{x}_{0}f'\left( {x}_{0}\right))
Η g είναι συνεχής και παραγωγίσιμη στο R αφού είναι και η f και ισχύει
=f'(x)-f'\left( {x}_{0}\right))
για κάθε
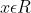
Για
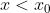
είναι
>0)
και για
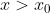
είναι
<0)
Η g είναι συνεχής στο
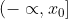
, παραγωγίσιμη στο
)
και ισχύει
>0)
για κάθε
)
. Συνεπώς η g είναι γνησίως αύξουσα στο
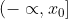
Η g είναι συνεχής στο
)
, παραγωγίσιμη στο
)
και ισχύει
<0)
για κάθε
)
. Συνεπώς η g είναι γνησίως φθίνουσα στο
)
.
Άρα η g παρουσιάζει ολικό μέγιστο στο
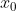
\leq g({x}_{0})\Rightarrow f(x)\leq xf'({x}_{0})+f({x}_{0})-{x}_{0}f'({x}_{0}))
για κάθε
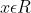
, που σημαίνει ότι η γραφική παράσταση της f βρίσκεται κάτω από την ευθεία της εφαπτομένης της στο σημείο
\right))
με μοναδικό κοινό σημείο το σημείο επαφής.
Αν υπάρχει ένα
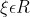
τέτοιο ώστε
=0)
τότε αυτό είναι μοναδικό καθώς η f' είναι γνησίως φθίνουσα, άρα και 1-1. Τότε
>f'(\xi )\Rightarrow f'(x)>0)
<f'(\xi )\Rightarrow f'(x)<0)
Δηλαδή σε αυτήν την περίπτωση ισχύει
>0)
για
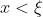
και
<0)
για
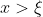
Άρα στην αυτή περίπτωση υπάρχουν
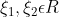
με
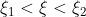
τέτοια ώστε
>0)
και
<0)
Αν
\neq 0)
για κάθε
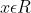
, τότε δεν είναι δυνατόν να υπάρχουν
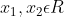
με
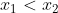
τέτοια ώστε
<0<f'({x}_{2}))
γιατί τότε σύμφωνα με το θεώρημα Darboux θα υπήρχε τουλάχιστον ένα
)
τέτοιο ώστε
=0)
(είτε είναι συνεχής είτε δεν είναι συνεχής η πρώτη παράγωγος της f στο
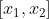
ισχύει αυτό. Το θεώρημα Darboux δεν το διδάσκεστε στο λύκειο)
Άρα σε αυτήν την περίπτωση η πρώτη παράγωγος f' της f διατηρεί σταθερό πρόσημο στο R που σημαίνει ότι η f είναι γνησίως μονότονη στο R. Δηλαδή ισχύει είτε f'(x)>0 για κάθε
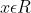
είτε f'(x)<0 για κάθε
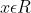
Σε κάθε περίπτωση, υπάρχει
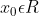
τέτοιο ώστε
\neq 0)
, οπότε είτε
>0)
είτε
<0)
Η εφαπτομένη της γαρφικής παράστασης της συνάρτησης f στο σημείο
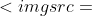
" /> παριστάνεται από την εξίσωση y=h(x) όπου h συνάρτηση με τύπο
=xf'({x}_{0})+f({x}_{0})-{x}_{0}f'({x}_{0}))
Αν
>0)
τότε έχουμε
<0\Rightarrow xf'({x}_{0})+f({x}_{0})-{x}_{0}f'({x}_{0})<0\Rightarrow x<\alpha )
όπου
-f({x}_{0})}{f'({x}_{0})})
Συνεπώς υπάρχει δ>0 τέτοιο ώστε
<0)
για κάθε
)
Συνεπώς επειδή
\leq h(x))
για κάθε
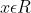
και
<0)
για κάθε
)
τότε
<0)
για κάθε
)
Αν
<0)
τότε έχουμε
<0\Rightarrow xf'({x}_{0})+f({x}_{0})-{x}_{0}f'({x}_{0})<0\Rightarrow x>\alpha )
όπου
-f({x}_{0})}{f'({x}_{0})})
Συνεπώς υπάρχει δ>0 τέτοιο ώστε
<0)
για κάθε
)
Συνεπώς επειδή
\leq h(x))
για κάθε
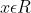
και
<0)
για κάθε
)
τότε
<0)
για κάθε
)
Άρα σε κάθε περίπτωση υπάρχει διάστημα Δ στο οποίο ισχύει f(x)<0 για κάθε