xf(y)+yf(x)=(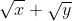
)f(xy)
x,y>1
f συνεχης
Να δειξετε οτι f(x)=0
Να πω παιδια οτι η ασκηση αυτη θεωρειτε πολυ δυσκολη και επιπλεον επειδη μου την εδωσε ενας συμμαθητης μου στο φροντιστηριο δεν ειμαι και βεβαιος αν ειναι ακριβως οπως την γραφει το βιβλιο απο οπου την βρηκε.
Γνωρίζουμε ότι η συνάρτηση f είναι ορισμένη και συνεχής στο (1,+οο) και ότι για κάθε x,y στο (1,+οο) ισχύει:
xf(y)+yf(x)=(SQRT(x)+SQRT(y))f(xy)
Για y=x>1 προκύπτει:
xf(x)+xf(x)=(SQRT(x)+SQRT(x))f(x*x) => 2xf(x)=2SQRT(x)f(x^2) => f(x^2)=f(x)SQRT(x), x>1
Επειδή η f είναι συνεχής στο (1,+οο) τότε για κάθε x0>1 ισχύει lim(x->x0)f(x)=f(x0)
Αν θέσουμε u=xy (x>1,y>1) τότε έχουμε:
lim(y->1+)(xy)=x*1=x
lim(y->1+)f(xy)=lim(u->x+)f(u)=f(x) εφόσον η f είναι συνεχής στο (1,+οο)
lim(y->1+)(SQRT(x)+SQRT(y))=SQRT(x)+SQRT(1)=SQRT(x)+1
Άρα lim(y->1+)[(SQRT(x)+SQRT(y))f(xy)]=[lim(y->1+)(SQRT(x)+SQRT(y))]*[lim(y->1+)f(xy)]=(SQRT(x)+1)f(x)
Από την αρχική συναρτησιακή εξίσωση, προκύπτει:
lim(y->1+)[xf(y)+yf(x)]=lim(y->1+)[(SQRT(x)+SQRT(y))f(xy)]
lim(y->1+)[xf(y)+yf(x)]=(SQRT(x)+1)f(x)
Για κάθε x,y στο (1,+οο) ισχύει η ταυτότητα:
f(y)=(xf(y)+yf(x)-yf(x))/x
Άρα
lim(y->1+)f(y)=lim(y->1+)[(xf(y)+yf(x)-yf(x))/x]=(1/x)*lim(y->1+)(xf(y)+yf(x)-yf(x))=
=(1/x)*[lim(y->1+)(xf(y)+yf(x))+lim(y->1+)(-yf(x))]=(1/x)*[lim(y->1+)(xf(y)+yf(x))-f(x)*lim(y->1+)y]=
=(1/x)*[(SQRT(x)+1)*f(x)-f(x)*1]=(1/x)*SQRT(x)*f(x)=f(x)/SQRT(x)
Άρα υπάρχει το lim(y->1+)f(y) και είναι πραγματικός αριθμός. Παρατηρούμε ότι lim(y->1+)f(y)=f(x)/SQRT(x)=g(x) που είναι αδύνατο καθώς θα πρέπει να είναι ένας σταθερός πραγματικός αριθμός και να μη μεταβάλλεται συναρτήσει του x. Άρα πρέπει να ισχύει lim(y->1+)f(y)=c όπου c ανήκει R. Συνεπώς προκύπτει:
lim(y->1+)f(y)=f(x)/SQRT(x) => c=f(x)/SQRT(x) => f(x)=c*SQRT(x), x>1
Αν αντικαταστήσουμε την συνάρτηση f(x)=c*SQRT(x) στην αρχική συναρτησιακή εξίσωση τότε παρατηρούμε ότι ικανοποιείται ταυτοτικά για κάθε x>1, y>1. Επίσης ικανοποιείται για κάθε x>1 όταν y->1+.
Άρα f(x)=c*SQRT(x), x>1 όπου c ανήκει R.
