Αυτό δεν ισχύει. Θα μπορούσε για παράδειγμα να είναι
=\begin{cases} \eta \mu ^2 x+ \eta \mu x + 1 & x < 0 \\ \eta \mu x- \eta \mu ^2 x-1 & x \geq 0 \end{cases})
Άλλωστε αν είχες εξαρχής αυτό το αποτέλεσμα, αυτό σημαίνει ότι θα ήξερες πως η f διατηρεί πρόσημο οπότε με βάση την τιμή
>0)
θα συμπέραινες ότι
=g(x) \,\,\,\forall x \in \mathbb{R})
και τελειώσαμε. Δεν θα χρειαζόταν δηλαδή ότι γράφεις παρακάτω.
Σωστή είναι η δεύτερη. Γενικά ισχύει το εξής:
Αν
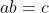
με
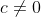
τότε ισχύει ότι
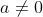
. Αυτό συμβαίνει γιατί αν το α ήταν 0 τότε προφανώς και το c θα ήταν 0, οποίο είναι άτοπο. Κατ' αναλογία έχουμε
(f(x)-2\eta\mu x)=\eta\mu^4 x+\eta \mu ^2 x+1)
με
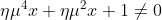
για κάθε
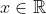
. Αυτό σημαίνει ότι
\neq 0)
για κάθε
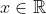
. Γιατί συμβαίνει αυτό; Γιατί αν υπήρχε
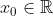
με
=0)
τότε αν βάλουμε στην σχέση όπου
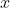
το
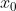
θα πάρουμε
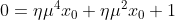
κάτι το οποίο είναι άτοπο.
Το υπερανάλυσα για να το χωνέψεις αλλά στην πραγματικότητα εκείνο που αρκεί να πεις είναι ότι εφ' όσον η παράσταση στο δεξί μέλος είναι διάφορη του 0 τότε υποχρεωτικά θα είναι και
\neq 0)
για κάθε
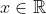
. Τα υπόλοιπα τα έχεις απλά στο μυαλό σου σαν εξήγηση.
Κι εδώ θα προσπαθήσω να είμαι αναλυτικός και ελπίζω να το πετύχω με το παρακάτω παράδειγμα. Ας θεωρήσουμε την συνάρτηση
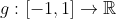
(το διάστημα [-1,1] είναι τυχαίο. Θα μπορούσα να πάρω κάποιο άλλο) για την οποία ισχύει ότι
=x^2+1)
για κάθε
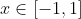
(*). Δεν ξέρω τίποτε άλλο γι'αυτήν πέρα απ' το ότι
 \neq 0)
αφού
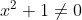
. Ούτε αν είναι συνεχής ούτε τίποτα. Αν σου έλεγα να μου βρεις κάποιες τέτοιες συναρτήσεις που ικανοποιούν τις υποθέσεις (*) ποια θα ήταν η απάντησή σου;
Η
=\sqrt{x^2+1}\,\,\,x \in [-1,1])
; Βεβαίως!
Η
=-\sqrt{x^2+1}\,\,\,x \in [-1,1])
; Γιατί όχι;!
Μήπως η
=\begin{cases}-\sqrt{x^2+1} & x \in [-1,0) \\ \sqrt{x^2+1} & x \in [0,1]\end{cases})
Φαίνεται λίγο περίεργη αλλά και αυτή την κάνει την δουλειά. Ας πάρουμε αυτή την τελευταία να την δούμε λίγο προσεκτικά.
Αυτή η συνάρτηση λοιπόν η τελευταία τι χαρακτηριστικά έχει; Ισχύει για παράδειγμα ότι
 \neq 0 \,\,\, \forall x \in [-1,1])
. Φυσικά! Δεν μηδενίζεται πουθενά, φαίνεται άλλωστε. Διατηρεί πρόσημο στο [-1,1];
ΟΧΙ Για άλλες τιμές είναι θετική για άλλες αρνητική.
Τι άλλο μπορούμε να πούμε για την
; Δεν είναι συνεχής σε όλο το διάστημα [-1,1] . Πράγματι η
δεν είναι συνεχής στο 0 αφού
=-1 \neq 1=\lim_{x \to 0^+}g(x))
. Αυτές οι τρεις συναρτήσεις λοιπόν όλες ικανοποιούν τις υποθέσεις (*), άρα η απάντηση θα μπορούσε να είναι οποιαδήποτε από αυτές.
Ας προσθέσουμε τώρα στις (*) την επιπλέον υπόθεση της συνέχειας για την g σε όλο το [-1,1] και ας ονομάσουμε τις καινούριες υποθέσεις (**). Τι άλλαξε τώρα; Μπορώ να δεχθώ πλέον την
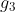
σαν υποψήφια συνάρτηση; Φυσικά και όχι, αφού αυτή δεν είναι συνεχής όπως είδαμε. Η g που ψάχνω πλέον είναι συνεχής και διάφορη του 0 στο διάστημα [-1,1]. Άρα λόγω του γνωστού πορίσματος (σελ 192 πρώτο σχόλιο μετά το θεώρημα Βοlzano ) θα διατηρεί πρόσημο στο [-1,1]. Τι σημαίνει αυτό; Θα είναι είτε
>0,\,\,\forall x \in [-1,1])
οπότε
=g_1(x) \,\,\, x \in [-1,1])
είτε
<0,\,\,\forall x \in [-1,1])
οπότε
=g(x_2)\,\,\, x \in [-1,1])
. Χμ αν είχα μαζί με τις υποθέσεις (**) και μία τιμή για την g για κάποιο
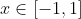
ίσως να μπορούσα τελικά να καταλήξω στον τύπο της g. Πχ αν μου δίνει
=1>0)
μπορώ με σιγουριά να πω ότι
=g_1(x) \,\,\, x \in [-1,1])
. Άρα λοιπόν και για να απαντήσω επιτέλους στο ερώτημα που έβαλες, η συνέχεια σ'αυτές τις περιπτώσεις είναι καταλυτική. Μου εξασφαλίζει
μέσω του πορίσματος του Bolzano ότι μία συνάρτηση με άγνωστο τύπο, που δεν μηδενίζεται πουθενά σε ένα διάστημα και συνεχής, θα βρίσκεται είτε ολόκληρη πάνω από τον άξονα των χ είτε ολόκληρη κάτω απ' αυτόν. Ότι δεν θα σπάει δηλαδή σε ασυνεχή κομμάτια όπως στην περίπτωση της
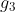
Το ότι διατηρεί πρόσημο το συμπεραίνεις
α) Επειδή έχεις δείξει ότι
 \neq 0)
για κάθε χ πραγματικό.
β) Επειδή η f είναι συνεχής στους πραγματικούς.
Μέχρι τώρα λοιπόν ξέρουμε ότι είτε
>0 \,\, \forall x \in \mathbb{R})
είτε
<0 \,\, \forall x \in \mathbb{R})
Για να αποφασίσουμε τι από τα δύο ισχύει τελικά πρέπει οπωσδήποτε να ξέρω την τιμή της f σε ένα οποιοδήποτε σημείο. Το πρόσημο της τιμής αυτής θα είναι προφανώς και το πρόσημο όλων των τιμών της f (αφού είπαμε η f διατηρεί πρόσημο). Εδώ έχουμε
=3>0)
άρα υποχρεωτικά
>0 \,\, \forall x \in \mathbb{R})
.
Απορίες;
