Civilara
Περιβόητο μέλος


μπορει να με βοηθησει κανενας??
Να βρεθει ο γεωμετρικος τοπος των σημειων Μ(χ,y) του επιπεδου για τα οποια ισχυει : x(στη τριτη) + y(στην τριτη) + x(τετραγωνο)*y + x*y(τετραγωνο) =x+y
*=(επι)
Σωστή μέχρι ενός σημείου η απάντηση του tebelis13 αλλά δεν έχει βρει όλα τα σημεία του ζητούμενου γεωμετρικού τόπου. Εγώ θα επιχειρήσω μια άλλη προσέγγιση με μετασχηματισμό σε πολικές συντεταγμένες που ξεφεύγει κάπως από τη σχολική ύλη.
Οι πολικές συντεταγμένες του σημείου M(x,y) δίνονται από τις σχέσεις:
x=ρ*συνφ
y=ρ*ημφ
όπου για οποιοδήποτε σημείο του επιπέδου Oxy, με εξαίρεση την αρχή Ο(0,0), είναι ρ=(ΟΜ)>0 και 0<=φ<2π η αριστερόστροφη γωνία (αντίθετα από τους δείκτες του ρολογιού) που σχηματίζει το μοναδιαίο διάνυσμα i στον θετικό ημιάξονα Ox με την διανυσματική ακτίνα ΟΜ. Για την αρχή Ο(0,0) είναι ρ=0 και δεν ορίζεται φ.
Αντικαθιστώντας στην αρχική εξίσωση έχουμε:
x^3+y^3+x^2y+xy^2=x+y
(ρσυνφ)^3+(ρημφ)^3+(ρσυνφ)^2ρημφ+ρσυνφ(ρημφ)^2=ρσυνφ+ρημφ
(ρ^3)συν^3φ+(ρ^3)ημ^3φ+(ρ^3)ημφσυν^2φ+ρ^3ημ^2φσυνφ=ρ(ημφ+συνφ)
(ρ^3)(συν^3φ+ημφσυν^2φ+ημ^3φ+ημ^2φσυνφ)-ρ(ημφ+συνφ)=0
(ρ^3)[συν^2φ(ημφ+συνφ)+ημ^2φ(ημφ+συνφ)]-ρ(ημφ+συνφ)=0
(ρ^3)(ημφ+συνφ)(ημ^2φ+συν^2φ)-ρ(ημφ=συνφ)=0
(ρ^3)(ημφ+συνφ)-ρ(ημφσυνφ)=0
ρ(ρ^2-1)(ημφ+συνφ)=0
α) Αν ρ=0 τότε x=y=0, οπότε η αρχή Ο(0,0) είναι σημείο του γεωμετρικού τόπου
β) Αν ρ^2-1=0 => ρ^2=1 τότε ρ=1 αφού ρ>0 που είναι η εξίσωση κύκλου (ρ=σταθερό) με ακτίνα R=1 και κέντρο την αρχή Ο(0,0). Δηλαδή τα σημεία της περιφέρειας του κύκλου με εξίσωση x^2+y^2=1 είναι σημεία του γεωμετρικού τόπου
γ) ημφ+συνφ=0 <=> ημφ=-συνφ
Αν συνφ=0 τότε θα ήταν και ημφ=0 αφού ημφ=-συνφ που είναι άτοπο γιατί τότε θα ήταν ημ^2φ+συν^2φ=0 διάφορο 1. Άρα συνφ διάφορο 0 και συνεπώς ημφ διάφορο 0. Επομένως έχουμε ισοδύναμα:
ημφ=-συνφ <=> εφφ=-1 <=> εφφ=-εφπ/4 <=> εφφ=εφ(-π/4) <=> φ=κπ-π/4 όπου κ ανήκει Z
0<=φ<2π => 0<=κπ-π/4<2π => π/4<κπ<9π/4 => 1/4<κ<9/4 => κ=1 ή κ=2
Αν κ=1 τότε φ=π-π/4=3π/4, οπότε
ημφ=ημ3π/4=ημ(π-π/4)=ημπ/4=SQRT(2)/2
συνφ=συν3π/4=συν(π-π/4)=-συνπ/4=-SQRT(2)/2
x=ρσυνφ=-(SQRT(2)/2)ρ
y=ρημφ=(SQRT(2)/2)ρ
Από τις 2 τελευταίες σχέσεις προκύπτει με απαλοιφή του ρ ότι x=-y => y=-x. Επειδή είναι ρ>0 η λύση αυτή περιλαμβάνει τα σημεία της ευθείας y=-x όπου x<0.
Αν κ=2 τότε φ=2π-π/4=7π/4, οπότε
ημφ=ημ7π/4=ημ(2π-π/4)=ημ(-π/4)=-ημπ/4=-SQRT(2)/2
συνφ=συν7π/4=συν(2π-π/4)=συν(-π/4)=συνπ/4=SQRT(2)/2
x=ρσυνφ=(SQRT(2)/2)ρ
y=ρημφ=-(SQRT(2)/2)ρ
Από τις 2 τελευταίες σχέσεις προκύπτει με απαλοιφή του ρ ότι y=-x. Επειδή είναι ρ>0 η λύση αυτή περιλαμβάνει τα σημεία της ευθείας y=-x όπου x>0.
Επομένως ο ζητούμενος γεωμετρικός τόπος αποτελείται από όλα τα σημεία του κύκλου x^2+y^2=1 και της ευθείας y=-x. Δηλαδή ισχύει (x+y)(x^2+y^2-1)=0.
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
antwwwnis
Διάσημο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
vimaproto
Πολύ δραστήριο μέλος


Ενας τρόπος είναι αυτός που λέει ο Κώστας τον οποίο εγώ εφαρμόζω σπάνια.Ναι αλλά δεν μου αντιγράφονται...
Και δεν μπορώ να πατήσω εκεί που λέει αντιγραφή στο πρόχειρο...
Να σου πω τι κάνω εγώ.(Με την ευκαιρία ούτε και μένα λειτουργεί το αποθήκευση στο πρόχειρο)
Λοιπόν Αφού γράψω αυτά που θέλω με Αγγλικούς χαρακτήρες (τους Ελληνικούς δεν τους γράφεις από το πληκτρολόγιο αλλά, από το πινακάκι με τα γράμματα του Latex) πατώ "προεπισκόπηση"
Πηγαίνω τον κάρσορα στο δεξιό μέρος αυτού που εμφανίζεται από κάτω , και πατημένο το αριστερό κλικ , σέρνω τον κάρσορα προς τα αριστερά. Η Παράσταση γίνεται μπλε. Πατώ πάνω σαυτή δεξιό κλικ και αντιγραφή.
Γυρίζω στο κείμενο που έγραφα και κάνω επικόλληση. Αυτό κάνω μεταφερόμενος συνεχώς μεταξύ πίνακα κειμένου και πίνακα Latex.
Σημείωση. Οταν το κείμενο στο Latex είναι πολύ μεγάλο, πιθανόν να μη το σαρώνει για την αντιγραφή. Τότε αντέγραψε τμηματικά, δηλ με μικρές συναρτήσεις.
Μερικές φορές το σύστημα κολλάει και δεν κάνει αντιγραφή. Αν εξακολουθεί να υπάρχει πρόβλημα εφάρμοσε αυτό που λέει ο Κώστας
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Mercury
Επιφανές μέλος


Οταν δεν μας δινουν το α.Πως διαλεγουμε το καταλληλοτερο α για να κανουμε παραγοντοποιηση??
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Αν κανένας από αυτούς δεν είναι ρίζα του πολυωνύμου δεν σημαίνει ότι δεν έχει καθόλου ρίζες. Σημαίνει ότι δεν έχει ακέραιες ρίζες. Παράδειγμα
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
vimaproto
Πολύ δραστήριο μέλος


Να προσθέσω ότι το σχήμα Horner όπως το μαθαίνουν στο σχολείο λύνει το μισό πρόβλημα (ακέραιες ρίζες) Τις ρητές-αν υπάρχουν - τις αναζητούμε ως πηλίκο των διαιρετών του γνωστού όρου προς τους διαιρέτες του συντελεστή του μεγιστοβαθμίου όρουΚοιτάς τους διαιρέτες του σταθερού όρου και ελπίζεις κάποιος από αυτούς να είναι ρίζα του πολυωνύμου. Για παράδειγμα αν ο σταθερός όρος είναι ο 6 τότε υποψήφιες ακέραιες ρίζες του πολυωνύμου είναι οι 1,-1,2,-2,3,-3,6,-6 . Αν κάποιος από αυτούς είναι ρίζα του πολυωνύμου τότε αυτόν χρησιμοποιείς για α.
Αν κανένας από αυτούς δεν είναι ρίζα του πολυωνύμου δεν σημαίνει ότι δεν έχει καθόλου ρίζες. Σημαίνει ότι δεν έχει ακέραιες ρίζες. Παράδειγμα
(3x-1))
Στο 6χ²-5χ+1=0 οι πιθανές ρίζες είναι +- 1, +- 1/3, +- ½ , +- 1/6
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Mercury
Επιφανές μέλος


Κοιτάς τους διαιρέτες του σταθερού όρου και ελπίζεις κάποιος από αυτούς να είναι ρίζα του πολυωνύμου. Για παράδειγμα αν ο σταθερός όρος είναι ο 6 τότε υποψήφιες ακέραιες ρίζες του πολυωνύμου είναι οι 1,-1,2,-2,3,-3,6,-6 . Αν κάποιος από αυτούς είναι ρίζα του πολυωνύμου τότε αυτόν χρησιμοποιείς για α.
Αν κανένας από αυτούς δεν είναι ρίζα του πολυωνύμου δεν σημαίνει ότι δεν έχει καθόλου ρίζες. Σημαίνει ότι δεν έχει ακέραιες ρίζες. Παράδειγμα
(3x-1))
Χαζη ερωτησουλα:ο σταθερος ορος ποιος ειναι??
πχ.
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Guest 018946
Επισκέπτης


Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Rempeskes
Επιφανές μέλος


Γνωριζετε αν ισχυει το κριτηριο παρεμβολης για συναρτησεις με περισσοτερες απο μια μεταβλητες?
yeap.
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
maria....
Πολύ δραστήριο μέλος


Σταθερός όρος είναι ο συντελεστής τουΧαζη ερωτησουλα:ο σταθερος ορος ποιος ειναι??
πχ.
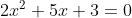
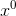
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Mercury
Επιφανές μέλος


Σταθερός όρος είναι ο συντελεστής του, οπού στο παράδειγμα που παρέθεσες είναι το 3.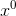
Σας ευχαριστω πολυ!!!


Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
mary-blackrose
Εκκολαπτόμενο μέλος


1) δινεται η εξισωση χ(τετραγωνο)+ψ(τετραγωνο)+4χ-2λψ=0 , λ ανηκει R
ι Ν.Δ.Ο. για καθε λ ανηκει R η εξισωση παριστανει κυκλο
ιι Ν.Δ.Ο το κεντρο του κυκλου βρισκεται πανω σε σταθερη ευθεια
ιιι για ποια τιμη του λ ο κυκλος εχει ακτινα ρ = ριζα 20;
ιν για ποια τιμη του λ ο κυκλος διερχεται απο το σημειο Α (-λ,1);
ν για ποια τιμη του λ ο κυκλος εφαπτεται του αξονα ψ'ψ;
νι να βρεθει ο γεωμετρικος τοπος των κεντρων των κυκλων
νιι Ν.Δ.Ο ολοι οι κυκλοι διερχονται απο δυο σταθερα σημεια
2)δινεται η εξισωση χ(χ-1)+ψ(ψ-1)=λ(χ+ψ-1) , λ ανηκει R
ι ν.δ.ο η εξισωση παριστανει κυκλο ο οποιος διερχεται απο τα σημεια Α(1,0) και Β(0,1)
ιι να βρειτε την εξισωση του κυκλου ο οποιος εχει το κεντρο του στην ευθεια χ+2ψ-6=0
ιιι για ποια τιμη του λ οι κυκλοι εφαπτονται στον αξονα χ'χ
ξερω οτι τα ερωτηματα ειναι
 παρα πολλα και ειναι δυσκολο και κουραστικο ν απαντηθουν ολα
παρα πολλα και ειναι δυσκολο και κουραστικο ν απαντηθουν ολα ....οποιος γνωριζει κατι ας με βοηθησει εστω και σε ενα απο αυτα......
....οποιος γνωριζει κατι ας με βοηθησει εστω και σε ενα απο αυτα......ευχαριστω... προκαταβολικα
 !
!Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
vimaproto
Πολύ δραστήριο μέλος


Παραείναι πολλάΜηπως μπορει καποιος να με βοηθησει σε δυο ασκησεις:
1) δινεται η εξισωση χ(τετραγωνο)+ψ(τετραγωνο)+4χ-2λψ=0 , λ ανηκει R
ι Ν.Δ.Ο. για καθε λ ανηκει R η εξισωση παριστανει κυκλο
ιι Ν.Δ.Ο το κεντρο του κυκλου βρισκεται πανω σε σταθερη ευθεια
ιιι για ποια τιμη του λ ο κυκλος εχει ακτινα ρ = ριζα 20;
ιν για ποια τιμη του λ ο κυκλος διερχεται απο το σημειο Α (-λ,1);
ν για ποια τιμη του λ ο κυκλος εφαπτεται του αξονα ψ'ψ;
νι να βρεθει ο γεωμετρικος τοπος των κεντρων των κυκλων
νιι Ν.Δ.Ο ολοι οι κυκλοι διερχονται απο δυο σταθερα σημεια
2)δινεται η εξισωση χ(χ-1)+ψ(ψ-1)=λ(χ+ψ-1) , λ ανηκει R
ι ν.δ.ο η εξισωση παριστανει κυκλο ο οποιος διερχεται απο τα σημεια Α(1,0) και Β(0,1)
ιι να βρειτε την εξισωση του κυκλου ο οποιος εχει το κεντρο του στην ευθεια χ+2ψ-6=0
ιιι για ποια τιμη του λ οι κυκλοι εφαπτονται στον αξονα χ'χ
ξερω οτι τα ερωτηματα ειναιπαρα πολλα και ειναι δυσκολο και κουραστικο ν απαντηθουν ολα
....οποιος γνωριζει κατι ας με βοηθησει εστω και σε ενα απο αυτα......
ευχαριστω... προκαταβολικα!
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Συνημμένα
Sansy16
Νεοφερμένο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
mary-blackrose
Εκκολαπτόμενο μέλος


δινεται κυκλος
1) να βρεθει η εφαπτομενη στο κυκλο στο σημειο Α (2,4).
2)να βρεθει η εφαπτομενη που ειναι παραλληλη στην εφαπτομενη που βρηκατε στο σημειο Α.
3)να βρεθουν οι εφαπτομενες που περνουν απο το Ο(0,0).
το πρωτο ερωτημα το εχω λυσει και το αποτελεσμα που μου βγηκε ειναι χ+ψ-6=0.Εχω λυσει και το δευτερο αλλα δεν ειμαι σιγουρη για τον τροπο λυσης μου,για αυτο αν μπορει κανεις να μου δωσει μια υποδειξη ή να μου περιγραψει τον τροπο λυσης στο δευτερο κ τριτο ερωτημα θα με βοηθησει παρα πολυ.

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
gregory nub
Διάσημο μέλος


Λοιπόν στο δεύτερο ερώτημα, θα έχεις απο το πρώτο εξίσωση μορφής ψ=λχ+β.γεια σας παιδια θα ηθελα μια βοηθεια-υποδειξη στη παρακατω ασκηση.:
δινεται κυκλος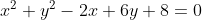
1) να βρεθει η εφαπτομενη στο κυκλο στο σημειο Α (2,4).
2)να βρεθει η εφαπτομενη που ειναι παραλληλη στην εφαπτομενη που βρηκατε στο σημειο Α.
3)να βρεθουν οι εφαπτομενες που περνουν απο το Ο(0,0).
το πρωτο ερωτημα το εχω λυσει και το αποτελεσμα που μου βγηκε ειναι χ+ψ-6=0.Εχω λυσει και το δευτερο αλλα δεν ειμαι σιγουρη για τον τροπο λυσης μου,για αυτο αν μπορει κανεις να μου δωσει μια υποδειξη ή να μου περιγραψει τον τροπο λυσης στο δευτερο κ τριτο ερωτημα θα με βοηθησει παρα πολυ.
κρατάς το λ και κάνεις τον τύπο απόστασης απο το κέντρο του κύκλου με την εφαπτομένη, θα σου βγουν 2 ευθείες, η μία θα είναι αυτή που ήδη έχεις και η άλλη η παράλληλη.
Όσον αφορά την τρίτη, παίρνεις τα σημεία που εφάπτονται οι 2 ευθείες μορφής ψ=λχ, τα βαφτίζεις (στο όνομα του Θεού
 ) και ύστερα αφού ξέρεις πως σχηματίζεται ορθή γωνία κάνεις τον νόμο του εσωτερικού γινομένου διανυσμάτων ( το προτείνω) ή πυθαγόρειο.
) και ύστερα αφού ξέρεις πως σχηματίζεται ορθή γωνία κάνεις τον νόμο του εσωτερικού γινομένου διανυσμάτων ( το προτείνω) ή πυθαγόρειο.Καλή τύχη.
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
*Serena*
Τιμώμενο Μέλος


λοιπον το κεντρο ειναι το (1,-3) οποτε το συμμετρικο του Α ως προς το κεντρο ειναι το Α' ( -1,-10) και βρισκεις την εφαπτομενη σε αυτο το σημειο. το αλλο ερωτημα θα κανω το σχημα, θα το σκεφτω και θα απαντησω σε λιγογεια σας παιδια θα ηθελα μια βοηθεια-υποδειξη στη παρακατω ασκηση.:
δινεται κυκλος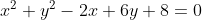
1) να βρεθει η εφαπτομενη στο κυκλο στο σημειο Α (2,4).
2)να βρεθει η εφαπτομενη που ειναι παραλληλη στην εφαπτομενη που βρηκατε στο σημειο Α.
3)να βρεθουν οι εφαπτομενες που περνουν απο το Ο(0,0).
το πρωτο ερωτημα το εχω λυσει και το αποτελεσμα που μου βγηκε ειναι χ+ψ-6=0.Εχω λυσει και το δευτερο αλλα δεν ειμαι σιγουρη για τον τροπο λυσης μου,για αυτο αν μπορει κανεις να μου δωσει μια υποδειξη ή να μου περιγραψει τον τροπο λυσης στο δευτερο κ τριτο ερωτημα θα με βοηθησει παρα πολυ.
 ουπς λαθος υπολογισμοι... ο τροπος ομως νομιζω ειναι σωστος...
ουπς λαθος υπολογισμοι... ο τροπος ομως νομιζω ειναι σωστος...Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
mary-blackrose
Εκκολαπτόμενο μέλος



Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
bond_bill
Νεοφερμένο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
vimaproto
Πολύ δραστήριο μέλος


Την άσκηση δεν την ξέρω γιατί δεν έχω το βιβλίοκαλησπερα προσπαθω να λυσω την ασκηση 3 ομαδα β στην ελλειψη. μετα απο αρκετη ωρα προσπαθεια χωρις αποτελεσμα κατεφυγα να δω την απαντηση στο λυσαρη του σχολειου. απλα δεν βγαζω ακρη απο αυτα που λεει. εδω ειναι το λυσαρη σελ 88 αυτο το r' στο τετραγωνο - r στο τετραγωνο=4γx ειναι τυπος ? που τον βρηκε ? επισης εγω προβλημα με την ασκηση 6 ομαδα β στο ιδιο κεφαλαιο οποιο βοηθεια ευπροσδεκτη
Θα προσπαθήσω να σου εξηγήσω τη γράφει το λυσάρι
r+r'=2α είναι από τον ορισμό της έλλειψης. Ελλειψη είναι ο Γεωμ. Τόπος των σημείων του επιπέδου που απέχουν από δύο σταθερά σημεία (Εστίες με συντεταγμένες Ε(γ,ο) , Ε' (-γ,0) ) σταθερή απόσταση =2α
Η απόσταση μεταξύ δύο σημείων Α και Β μάθατε ότι είναι (ΑΒ)²=(ΧΒ-ΧΑ)²+(YB-YA)². Αρα ένα σημείο Μ πάνω στην έλλειψη με συντεταγμένες (χ,y) Απέχει από τη μία εστία r=ME και από την άλλη r'=ME' και ισχύουν r²=(x-γ)²+y² και r'²=[χ-(-γ)]²+y²=)χ+γ)²+y²
Η συνέχεια δική σου, είναι αλγεβρικές πράξεις.
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
- Status
- Το θέμα δεν είναι ανοιχτό για νέες απαντήσεις.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 1 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 16 μέλη διάβασαν αυτό το θέμα:
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki




