1. Θεωρούμε την
=\alpha x^3+\beta x^2+3x+\beta ^2,\alpha ,\beta \in R)
. Αν η f παρουσιάζει τοπικά ακρότατα στα σημεία
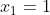
και
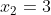
, τότε:
α) να αποδειχθεί ότι
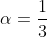
και
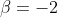
,
β) να μελετηθεί η f ως προς τη μονοτονία και τα ακρότατα
f(x)=α(x^3)+β(x^2)+3x+β^2
α) Η συνάρτηση f είναι συνεχής και παραγωγίσιμη στο R ως πολυωνυμική με πρώτη παράγωγο:
f΄(x)=3α(x^2)+2βx+3, x ανήκει R
Επειδή συνάρτηση f παρουσιάζει τοπικά ακρότατα στα σημεία x1=1 και x2=3 και είναι παραγωγίσιμη σε αυτά τότε σύμφωνα με το θεώρημα του Fermat ισχύει f΄(1)=f΄(3)=0. Έχουμε:
f΄(1)=3α+2β+3
f΄(3)=27α+6β+3=3(9α+2β+1)
f΄(1)=0 <=> 3α+2β+3=0 <=> β=-((3α+3)/2) (1)
f΄(3)=0 <=> 9α+2β+1=0 <=> β=-((9α+1)/2) (2)
Από τις (1) και (2) προκύπτει ότι
-((3α+3)/2)=-((9α+1)/2) <=> 3α+3=9α+1 <=> 6α=2 <=> α=1/3
Αντικαθιστώντας σε οποιαδήποτε από τις (1) και (2) προκύπτει ότι β=-2
Επομένως f(x)=(1/3)(x^3)-2(x^2)+3x+4
β)
f(x)=(1/3)(x^3)-2(x^2)+3x+4
f΄(x)=(x^2)-4x+3=(x-1)(x-3)
Η συνάρτηση f είναι συνεχής στο (-άπειρο,1], παραγωγίσιμη στο (-άπειρο,1) και ισχύει f΄(x)>0 για κάθε x στο (-άπειρο,1). Επομένως η συνάρτηση f είναι γνησίως αύξουσα στο (-άπειρο,1].
Η συνάρτηση f είναι συνεχής στο [1,3], παραγωγίσιμη στο (1,3) και ισχύει f΄(x)<0 για κάθε x στο (1,3). Επομένως η συνάρτηση f είναι γνησίως φθίνουσα στο (1,3].
Η συνάρτηση f είναι συνεχής στο [3,+άπειρο), παραγωγίσιμη στο (3,+άπειρο) και ισχύει f΄(x)>0 για κάθε x στο (3,+άπειρο). Επομένως η συνάρτηση f είναι γνησίως αύξουσα στο (3,+άπειρο].
Συνεπώς η συνάρτηση f παρουσιάζει τοπικό μέγιστο στο x1=1 με τιμή f(1)=16/3 και τοπικό ελάχιστο στο x2=3 με τιμή f(3)=4
2. Δίνεται η
=x^2+2\alpha x+4\alpha ,\alpha \in R)
. Να βρεθούν:
α) η ελάχιστη τιμή της f
β) η τιμή του α για την οποία η ελάχιστη τιμή της f γίνεται μέγιστη.
f(x)=(x^2)+2αx+4α, x ανήκει R
α) Η συνάρτηση f είναι συνεχής και παραγωγίσιμη στο R ως πολυωνυμική με πρώτη παράγωγο f΄(x)=2x+2α=2(x+α)
Η μοναδική ρίζα της εξίσωσης f΄(x)=0 είναι η x=-α.
Η συνάρτηση f είναι συνεχής στο (-άπειρο,-α], παραγωγίσιμη στο (-άπειρο,-α) και ισχύει f΄(x)<0 για x ανήκει στο (-άπειρο,-α). Επομένως η συνάρτηση f είναι γνησίως φθίνουσα στο (-άπειρο,α].
Η συνάρτηση f είναι συνεχής στο [-α,+άπειρο), παραγωγίσιμη στο (-α,+άπειρο) και ισχύει f΄(x)>0 για x ανήκει στο (-α,+άπειρο). Επομένως η συνάρτηση f είναι γνησίως αύξουσα στο [-α,+άπειρο).
Συνεπώς η συνάρτηση f παρουσιάζει ολικό ελάχιστο στο x0=-α με τιμή f(-α)=-(α^2)+4α
β) Θεωρώ την συνάρτηση g(α)=f(-α)=-(α^2)+4α, α ανήκει R
Η συνάρτηση g είναι συνεχής και παραγωγίσιμη στο R ως πολυωνυμική με πρώτη παράγωγο g΄(α)=-2α+4=2(2-α)
Παρατηρούμε ότι g΄(2)=0 και η εξίσωση g΄(α)=0 δεν έχει άλλη ρίζα
Η συνάρτηση g είναι συνεχής στο (-άπειρο,2], παραγωγίσιμη στο (-άπειρο,2) και ισχύει g΄(x)>0 για x ανήκει στο (-άπειρο,2). Επομένως η συνάρτηση g είναι γνησίως αύξουσα στο (-άπειρο,2].
Η συνάρτηση g είναι συνεχής στο [2,+άπειρο), παραγωγίσιμη στο (2,+άπειρο) και ισχύει g΄(x)>0 για x ανήκει στο (2,+άπειρο). Επομένως η συνάρτηση g είναι γνησίως αύξουσα στο [2,+άπειρο).
Συνεπώς η συνάρτηση g παρουσιάζει ολικό μέγιστο στο x3=2 με g(2)=f(-2)=4