eukleidhs1821
Διάσημο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Earendil
Νεοφερμένο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Μάρκος Βασίλης
Πολύ δραστήριο μέλος


ναι την ακουσα την οδηγια αυτη ομως δεν νομιμοποιουνται να βαλουν ενα οριο που απαιτει χρηση l hospital μονο γτ θεωρειται εκτος υλης.η οδηγια ειναι προς αυτους που θελουν να χρησιμοποιησουν ενα l hospital σε ορια που βγαινουν και με αλγεβρικο τεχνασμα και βαριουνται να χρησιμοποιησουν απλες ταυτοτητες απλα κανουνε απευθειας l hospital.εγω τουλαχιστον αυτο καταλαβα
Επιτρέπεται - με την έννοια ότι είναι και «οδηγία» προς τα Βαθμολογικά Κέντρα - να χρησιμοποιηθεί γνώση που αναφέρεται σε άλλο μέρος του βιβλίου άνευ απόδειξης.
Παιδιά genuine απορία. ο καθηγητής στο σχολειό μας ισχυρίζεται πως δεν θα έπρεπε να θεωρούμε τους εξής τύπους:
1. e^x>=x+1
2.lnx<=x-1
ως δεδομένους και θα πρέπει όταν τους χρησιμοποιούμε να τους αποδεικνύουμε πρώτα . Το οποίο καταλαβαίνω γιατί το κάνει -εξάλλου αποδευκνύονται πολυ εύκολα με την παράγωγο- ,από την άλλη στις πανελλήνιες που ο χρόνος μετράει αντίστροφα, δεν ξερώ αν αξίζει ο χρόνος. Για ποιο λόγο και ο μπάρλας και ο παπαδάκης ισχυρίζονται οτί τους τύπους αυτούς τους παίρνουμε ως γνωστούς? Δεν διαβάζω σχολικό βιβλίο( για ευνόητους λόγους) αλλά άμα κάποιος γνωρίζει τι παίζει σχετικά με αυτό το θέμα θα ήθελα πολύ να το αναφέρετε.
Πρώτον, κακώς δε διαβάζεις από το σχολικό - δε στο λέω για να νιώσεις άσχημα, μέρες που είναι, αλλά γιατί προλαβαίνεις να κάνεις ένα ξεσκόνισμα κι εκεί.
Δεύτερον, και οι δύο ανισότητες θεωρούνται γνωστές και τις χρησιμοποιείτε άνευ απόδειξης - δες την παράθεση της @Athena apo για τη σχετική οδηγία. Αυτοί οι τύποι έχουν κι ένα άλλο επιστημολογικό ενδιαφέρον που συνηγορεί υπέρ του να μη χρησιμοποιούνται με απόδειξη. Για να τους αποδείξει - τον δεύτερο - το σχολικό βιβλίο χρησιμοποιεί την παραγωγισιμότητα του λογαρίθμου. Ωστόσο - αναφέρομαι σε εκτός ύλης πράγματα τώρα - για να αποδειχθεί η παραγωγισιμότητα του λογαρίθμου χρησιμοποιείται η ανισότητα ln x <= x-1
πράγμα που καθιστά την απόδειξη του σχολικού βιβλίου κυκλική και άνευ νοήματος - το έχει επισημάνει και πριν από 2-3 χρόνια ο κ. Πολύζος σε σχετική του παρουσίαση στη Λιβαδειά. Η αλήθεια είναι ότι, originally, οι παραπάνω ανισότητες αποδεικνύονται με εργαλεία εκτός του λυκείου που δεν έχουν να κάνουν άμεσα με την παραγωγισιμότητα γι' αυτό και στο λύκειο προκύπτει αυτό το πρόβλημα.
TL;DR: Τις χρησιμοποιείς χωρίς να σε νοιάζει.
Πράγματι κυριολεκτικά κύκλοι γιατί το παίρνουν αβίαστα ως δεδομένο κατά την επίλυση .
Αλλά περίμενε, ένα λεπτό . Εαν μπορούσες να "μαγειρέψεις" ένα όριο που θα έπαιρνε σημαντικά πολύ χρόνο για να λυθεί και κατέληγε με την οριακή έκφραση του e και άντε πες κάτι να το πολλαπλασιάζει ή να το διαιρεί ;
Οπότε σε όσους έκοβε και το έβλεπαν ,θα γλίτωναν στο τέλος λίγο χρόνο . Δεν έχει πολύ κακές προοπτικές αυτή η εκδοχή νομίζω,ειδικά εαν τους είχε βγει λίγο η πίστη να καταλήξουν στην σωστή μορφή για να το αναγνωρίσουν. Και όσοι δεν το έβλεπαν,θα τους έβγαινε ακόμα παραπάνω η πίστη
.
Εντάξει, εκεί θα χάναμε το νόημα των εξετάσεων. :Ρ Σκέψου ότι στις οδηγίες το ΙΕΠ μας λέει να διδάσκουμε τα όρια με μόνη πρόθεση να αναδείξουμε βασικά όρια και την ιδέα. :Ρ
Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Samael
Τιμώμενο Μέλος


Επιτρέπεται - με την έννοια ότι είναι και «οδηγία» προς τα Βαθμολογικά Κέντρα - να χρησιμοποιηθεί γνώση που αναφέρεται σε άλλο μέρος του βιβλίου άνευ απόδειξης.
Πρώτον, κακώς δε διαβάζεις από το σχολικό - δε στο λέω για να νιώσεις άσχημα, μέρες που είναι, αλλά γιατί προλαβαίνεις να κάνεις ένα ξεσκόνισμα κι εκεί.
Δεύτερον, και οι δύο ανισότητες θεωρούνται γνωστές και τις χρησιμοποιείτε άνευ απόδειξης - δες την παράθεση της @Athena apo για τη σχετική οδηγία. Αυτοί οι τύποι έχουν κι ένα άλλο επιστημολογικό ενδιαφέρον που συνηγορεί υπέρ του να μη χρησιμοποιούνται με απόδειξη. Για να τους αποδείξει - τον δεύτερο - το σχολικό βιβλίο χρησιμοποιεί την παραγωγισιμότητα του λογαρίθμου. Ωστόσο - αναφέρομαι σε εκτός ύλης πράγματα τώρα - για να αποδειχθεί η παραγωγισιμότητα του λογαρίθμου χρησιμοποιείται η ανισότητα ln x <= x-1
πράγμα που καθιστά την απόδειξη του σχολικού βιβλίου κυκλική και άνευ νοήματος - το έχει επισημάνει και πριν από 2-3 χρόνια ο κ. Πολύζος σε σχετική του παρουσίαση στη Λιβαδειά. Η αλήθεια είναι ότι, originally, οι παραπάνω ανισότητες αποδεικνύονται με εργαλεία εκτός του λυκείου που δεν έχουν να κάνουν άμεσα με την παραγωγισιμότητα γι' αυτό και στο λύκειο προκύπτει αυτό το πρόβλημα.
TL;DR: Τις χρησιμοποιείς χωρίς να σε νοιάζει.
Εντάξει, εκεί θα χάναμε το νόημα των εξετάσεων. :Ρ Σκέψου ότι στις οδηγίες το ΙΕΠ μας λέει να διδάσκουμε τα όρια με μόνη πρόθεση να αναδείξουμε βασικά όρια και την ιδέα. :Ρ
Γιατί τέτοιο πετσόκομμα στα όρια ξαφνικά ; Πως διαφέρουν απο της γενικής πλέον άρα ;
Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Papachrist
Νεοφερμένο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
eukleidhs1821
Διάσημο μέλος


προσοχη φερματ κανεις στο 1 μην πεις στο μηδεν που δεν ειναι εσωτερικο σημειο το χασες το παιχνιδι αλλωστε φαινεται οτι δεν ειναι τοπικο ακροτατο στο μηδεν.
η υπολοιπη 3 κλασσικοτατη ασκηση θεμα πραξεων καθαρα.το 4 α θεμα παραγωγισεων καθαρα.
Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Papachrist
Νεοφερμένο μέλος


Αν μπορείτε να τα στείλετε σήμερα λίγο πιο αναλυτικά διότι μπερδεύομαι θα το εκτιμούσα κύριοι @Μάρκος Βασίλης @eukleidhs1821 @SamaelΕυχαριστώ ....αλλά θα μπορούσατε εσείς η ο κύριος @Μάρκος Βασίλης η ο @Samael λίγο πιο αναλυτικά παρακαλώ?
Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Μάρκος Βασίλης
Πολύ δραστήριο μέλος


Γιατί τέτοιο πετσόκομμα στα όρια ξαφνικά ; Πως διαφέρουν απο της γενικής πλέον άρα ;
Copy paste τις κάνει το ΙΕΠ τις οδηγίες κοντά μια δεκαετία. :Ρ Πάντα αυτά ίσχυαν απλά άλλες επιτροπές παλαιότερα ήταν πιο «ενδοτικές» στις άρρητες πιέσεις των φροντιστηρίων και απομακρύνονταν από το σχολικό βιβλίο. Θεωρητικά, ο στόχος όλης της Γ' λυκείου είναι να λύσουμε δύο προβλήματα:
- τη χάραξη της γραφική παράστασης παραγωγίσιμης συνάρτησης,
- τον υπολογισμό εμβαδών - ή/και έργων κ.λπ.
@Papachrist
- 3α) Γράψε τη σχέση ως εξής:
και ορισμούς για τα άλλα δύο.

- 3β) Έχει εύκολη παράγωγο, δε θα σε δυσκολέψει.
- 3γ) Εκτός από αυτό που σου είπε ο Ευκλείδης, σκέψου και το εξής: Έστω,
μία ευθεία και έστω η συνάρτηση
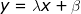 . Αν υποθέσουμε, προς άτοπο, ότι η g έχει τουλάχιστον τρεις ρίζες τότε με Rolle θα βρεις δύο για την παράγωγο και ξανά με Rolle θα βρεις μία για τη δεύτερη παράγωγο. Όμως
. Αν υποθέσουμε, προς άτοπο, ότι η g έχει τουλάχιστον τρεις ρίζες τότε με Rolle θα βρεις δύο για την παράγωγο και ξανά με Rolle θα βρεις μία για τη δεύτερη παράγωγο. Όμως , άτοπο.
, άτοπο.
- 3δ) Fermat.
- 4α) Πράξεις.
- 4β) Χρησιμοποίησε το γεγονός ότι
(ελπίζω να μην έκανα λάθος στις πράξεις).

- 4γ) Παρατήρησε ότι
- βγαίνει με πολλούς τρόπους - και άρα
 . Παρατήρησε τώρα ότι η συνάρτηση
. Παρατήρησε τώρα ότι η συνάρτηση είναι γνησίως αύξουσα και βγάλε το ζητούμενο.
είναι γνησίως αύξουσα και βγάλε το ζητούμενο.
- 4δ) Απαλοιφή παρονομαστών και θεωρείς συνάρτηση - μετά θέλει μαγείρεμα. Αν κολλήσεις με αυτόν τον τρόπο, βγαίνει κι αλλιώς.
Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
eukleidhs1821
Διάσημο μέλος


Α και ξεχασα και το μηκος του κυκλου!Τι να πω απορω τι μαθαινουνε τοσα χρονια στα σχολεια!Το πυθαγορειο θεωρημα φανταζομαι θα το ξερουν ολοι αφου το εφαρμοζουν και φυσικη.Κατι αλλο απο γεωμετρια δεν μου ρχεται.Α και τις επικεντρες γωνιες και τις εγγεγραμμενες προσεχτε μην γινει κανα τρελο και συνδεθει με ρυθμο μεταβολης ξερω γω.Επισης γραφικη παρασταση θα πεσει στανταρ μην τσιμπατε που τη βγαλαν εκτος.Απλα θα ειναι απο ετοιμες γραφικες και του στυλ f(x)+c.Σουπερ σος η γραφικη της ριζας χ.Μπορει να σου πουνε κανε τη γραφικη της ριζα χ-2
Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Earendil
Νεοφερμένο μέλος


διαβαστε ολους τους τυπους των εμβαδων!!Κυκλος,τετραγωνο,τραπεζιο,κυκλικος τομεας και εξισωσεις κωνικων τομων!!Ειναι πολυ πιθανο το τριτο θεμα να ειναι οπως το 2018.
Δεν γίνεται να βαλουν κυκλικό τομέα/κωνικές τομες/πυραμίδες και όλα αυτά εφόσον δεν υπάρχουν στο σχολικό βιβλίο (έτσι μου έχει πει ο καθηγητής μου) . Αν είναι να πέσουν,θα βάλουν κύκλο/τετραγώνο/ορθ τριγ./ορθ παρ/ορθ παρ.επ/τετραπλευρο etc.. Επίσης για να σου απαντήσω στις απορίες σου. Στα σχολεία μαθαίνουμε μαθηματική ανάλυση και την ευκλείδια γεωμετρία την έχουμε παραμελήσει (όπως και ο περισσοτερός κόσμος στο εξωτερικό) και μου φαίνεται πολύ λογικό καθώς πλέον υπάρχουν μηχανήματα που αυτοματοποίουν τις λειτουργίες αυτές. Εξάλλου, δεν υπάρχει ευκλείδια γεωμετρία -εύκολα- στην ζωή. Προφανώς ωστόσο και την χρειάζονται οι μηχανικοί ,οι μαθηματικοί και οι φυσικοί. Όλοι οι υπόλοιποι,μόνο τα βασικά χρείαζονται στην ζώη τους
Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
eukleidhs1821
Διάσημο μέλος


κατηγορηματικα οχι!!!δεν μιλησα για στερεομετρια!!Δεδομενα εφοσον δεν διδασκεται στο λυκειο δεν μπορουν να σου βαλουν!!Κυκλικο τομεα ανετοτατα μπορουν να σου βαλουν!!Νομιζω εχει και ασκηση το σχολικο σου βιβλιο!Μην κανεις το λαθος να τα υποτιμησεις γτ ενδεχεται να ειναι το τριτο θεμα αυτο οπως το 2018.Επισης κωνικες τομες μπορουν να πεσουν και πρεπει να τα ξερουν γτ ειναι υλη β λυκειου αρα διδαγμενα.Ενταξει πρεπει να σαι λιγο ψιλογκαντεμης για να πεσουν κωνικες τομες αλλα εισαι υποχρεωμενος να γνωριζεις τα βασικα!!Εξισωσεις δηλαδη και τα ρεστα!!Μιση ωρα υποθεση ειναι να κατσεις να τα διαβασεις!Απορω τι καθηγητες ειναι αυτοι που λενε τετοια λογια.Κριμα πραγματικαΔεν γίνεται να βαλουν κυκλικό τομέα/κωνικές τομες/πυραμίδες και όλα αυτά εφόσον δεν υπάρχουν στο σχολικό βιβλίο (έτσι μου έχει πει ο καθηγητής μου) . Αν είναι να πέσουν,θα βάλουν κύκλο/τετραγώνο/ορθ τριγ./ορθ παρ/ορθ παρ.επ/τετραπλευρο etc..
Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Earendil
Νεοφερμένο μέλος


Δεν θέλω να αναφέρω όνοματα,αλλα οι συγκεκριμένοι έστειλαν παίδια σε χαρβαρντ,mit , cambridge γιατί σε αντίθεση με καθήγητες που έχουν κόμπλεξ και βάζουν οτι πιο συνδυαστικό υπάρχει για να μπερδέψουν τα παιδιά. Ακομα γνωρίζουν οτι πράγματα όπως κωνικές τομές (που δεν έχω δει ποτέ στην ζώη μου), δεν χρείαζονται -πλεον- και άρα δεν χρείαζεται να φορτώνεται ο μαθήτης με πληροφορίες που του είναι άχρηστεςΑπορω τι καθηγητες ειναι αυτοι που λενε τετοια λογια.Κριμα πραγματικα

Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Μάρκος Βασίλης
Πολύ δραστήριο μέλος


Δεν γίνεται να βαλουν κυκλικό τομέα/κωνικές τομες/πυραμίδες και όλα αυτά εφόσον δεν υπάρχουν στο σχολικό βιβλίο (έτσι μου έχει πει ο καθηγητής μου) . Αν είναι να πέσουν,θα βάλουν κύκλο/τετραγώνο/ορθ τριγ./ορθ παρ/ορθ παρ.επ/τετραπλευρο etc.. Επίσης για να σου απαντήσω στις απορίες σου. Στα σχολεία μαθαίνουμε μαθηματική ανάλυση και την ευκλείδια γεωμετρία την έχουμε παραμελήσει (όπως και ο περισσοτερός κόσμος στο εξωτερικό) και μου φαίνεται πολύ λογικό καθώς πλέον υπάρχουν μηχανήματα που αυτοματοποίουν τις λειτουργίες αυτές. Εξάλλου, δεν υπάρχει ευκλείδια γεωμετρία -εύκολα- στην ζωή. Προφανώς ωστόσο και την χρειάζονται οι μηχανικοί ,οι μαθηματικοί και οι φυσικοί. Όλοι οι υπόλοιποι,μόνο τα βασικά χρείαζονται στην ζώη τους
Κυκλικός τομέας: Β' λυκείου, Γεωμετρία, Γ' λυκείου, άσκηση σχολικού.
Κωνικές τομές: Κύκλος, έλλειψη, παραβολή, υπερβολή, κατεύθυνση της Β'.
Είναι στην ύλη σας και υπάρχει η δυνατότητα να ζητηθούν - άσχετο που δεν είναι πιθανό. Αλλά δεν είναι έξω από την ύλη σας. Προφανώς, δε θα πάτε τώρα να ανοίγετε όλα τα βιβλία των προηγούμενων τάξεων να δείτε ασκήσεις, αλλά ως έννοιες μπορούν να ζητηθούν.
Δεν θέλω να αναφέρω όνοματα,αλλα οι συγκεκριμένοι έστειλαν παίδια σε χαρβαρντ,mit , cambridge γιατί σε αντίθεση με καθήγητες που έχουν κόμπλεξ και βάζουν οτι πιο συνδυαστικό υπάρχει για να μπερδέψουν τα παιδιά ,γνωρίζουν οτι πράγματα όπως κωνικές τομές (που δεν έχω δει ποτέ στην ζώη μου), δεν χρείαζονται -πλεον!- και άρα δεν χρείαζεται να φορτώνεται ο μαθήτης με πληροφορίες που του είναι άχρηστες
Κωνικές τομές έχεις δει στη ζωή σου. Broadly, βλέπεις το δορυφορικό πιάτο στην απέναντι ταράτσα που είναι παραβολοειδές, όπως και οι προβολείς των αυτοκινήτων. Έχεις δει και μία ολόκληρη χρονιά στην κατεύθυνση. :Ρ
Σε σχέση με το αν είναι χρήσιμα, η Ευκλείδεια Γεωμετρία όπως την έκανε ο Ευκλείδης - όχι ο δικός μας :Ρ - δεν είναι πρακτική, σε αντίθεση με την αναλυτική γεωμετρία που έχει αρκετές εφαρμογές. Αυτό δε σημαίνει ότι δε χρειάζεται να τη μάθεις - προτασιακή λογική κ.λπ., τα έχουμε ξαναπεί αυτά αλλού.
Τα θέματα, τα τελευταία χρόνια, δεν μπαίνουν για να σας μπερδέψουν, αλλά για να κάνουν την κατάλληλη κατανομή των μαθητών σε σχέση με τη μαθηματική τους παιδεία. Αν έχει ένα παιδί κενά από προηγούμενες τάξεις στις έννοιες και όχι στο ασκησιολόγιο λογικό μου φαίνεται να πρέπει να είναι τα θέματα των πανελλαδικών τέτοια ώστε να μπορεί κανείς να το διακρίνει αυτό. Όπως έγινε με την παραγώγιση της
Το θέμα είναι, τώρα, να τα αξιοποιήσουν και κάποια άτομα στο υπουργείο αυτά...
Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Samael
Τιμώμενο Μέλος


 . Πράγματι εαν έχεις διαβάσει πολύ καλά άλλους κλάδους των μαθηματικών ίσως να μπορέσεις να λύσεις δια της πλαγίου ένα γεωμετρικό πρόβλημα.
. Πράγματι εαν έχεις διαβάσει πολύ καλά άλλους κλάδους των μαθηματικών ίσως να μπορέσεις να λύσεις δια της πλαγίου ένα γεωμετρικό πρόβλημα.Όμως επειδή πρακτικά δεν είναι χρήσιμη δεν σημαίνει οτι δεν έχει οφέλη,εαν και έχει μια χαρά σοβαρές εφαρμογές,απλά δεν είναι γνωστές στον κόσμο .Μπορείς να εφαρμόσεις Λαγκρανζιανή μηχανική και να πετάξεις σχεδόν όλη την γεωμετρία σε αντίθεση με την νευτώνεια μηχανική . Ωστόσο ποιος μαθητής έχει το intuition για μια τέτοια θεωρία ; Και μάλιστα πόσο overkill θα ήταν η εφαρμογή της για απλά προβλήματα; Ορισμένες μαθηματικές τεχνικές και θεωρίες αποκτούν ιδιαίτερο advantage μόνο όταν το πρόβλημα σου αρχίζει και γίνεται πολύ περίπλοκο . Άρα οι απλές θεωρίες είναι χρήσιμες γιατί δίνουν μια διαίσθηση και επιλύουν εύκολα και γρήγορα ορισμένα προβλήματα . Ταυτόχρονα εξυπηρετούν ως σκαλοπάτι στην εκπαιδευτική διαδικασία , ώστε να πας την σκέψη σου σταδιακά μερικά κλικ πιο κάτω .
Γενικά και εγώ απ'όσο ξέρω διδάσκονται οι κωνικές τομές στην Β λυκείου και θυμάμαι τότε μας έλεγαν πως οτιδήποτε απο προηγούμενες τάξεις μπορούν να το βάλουν . Επομένως εγώ στην θέση σας θα τα διάβαζα σίγουρα για να έχω το κεφάλι μου ήσυχο . Καλύτερα να πας πολύ προετοιμασμένος παρά να νιώθεις οτι υπάρχουν σημεία που έχεις κενά .
Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
kvstas92
Νεοφερμένο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
eukleidhs1821
Διάσημο μέλος


δεν καταλαβαινω το ειρωνικο του μηνυματος.κωνικες τομες εννοω εξισωση κυκλου,ελλειψης παραβολης,υπερβολης.Αμα πεσει θεμα με κυκλικο τομεα και εμβαδον θελω να δω ο καθηγητης σου τι θα λεει.Δεν θέλω να αναφέρω όνοματα,αλλα οι συγκεκριμένοι έστειλαν παίδια σε χαρβαρντ,mit , cambridge γιατί σε αντίθεση με καθήγητες που έχουν κόμπλεξ και βάζουν οτι πιο συνδυαστικό υπάρχει για να μπερδέψουν τα παιδιά. Ακομα γνωρίζουν οτι πράγματα όπως κωνικές τομές (που δεν έχω δει ποτέ στην ζώη μου), δεν χρείαζονται -πλεον- και άρα δεν χρείαζεται να φορτώνεται ο μαθήτης με πληροφορίες που του είναι άχρηστες
οχι βεβαια!Τι να επαληθευσεις.Τη διαδικασια θα κανεις οπως τη γνωριζειςΚαλησπερα, θεωρειται πως οταν μας δινουνε μια ανισοτικη σχεση για παραδειγμα α^χ>= χ^α και μας λενε να βρουμε το α με φερματ θα πρεπει να γινει και επαληθευση? Δηλαδη αν θεωρησουμε συναρτηση και παρουσιαζει ελαχιστο θα πρεπει να βαλουμε για α την τιμη που θα βρουμε και να δειξουμε οτι παρουσιαζει ελαχιστο?
Οταν λεω γνωσεις απο προηγουμενες ταξεις δεν εννοω να καθισετε να διαβασετε μεθοδολογια ασκησεων με κωνικες τομες προφανως!!Αν ειναι δυνατον να πιστευετε αυτο!Αυτο που εννοω ειναι εξισωσεις κυκλου ,ελλειψης κτλπ.Δηλαδη τελειως χοντρικα να ξερετε παπαγαλιστι αν μπορουμε να παρουμε βασικα πραγματα!Με την ιδια λογικη δεν ξερετε τον συντελεστη διευθυνσης ευθειας επειδη διδασκοταν στη β λυκειου η ευθεια!Ξαναλεω ειναι κριμα να χασετε μορια επειδη δεν αφιερωσατε 30 λεπτα απο το χρονο σας να μαθετε μηχανικα καποιες εννοιες
Φετος προβλεπω οτι θα ερθει θεμα που θα ναι ενας φιλος απο τα παλια
 .Δηλαδη οριο με h και παραγωγο οπως το τεταρτο του 2008 σε αλλη μορφη που δε θα θελει l hospital
.Δηλαδη οριο με h και παραγωγο οπως το τεταρτο του 2008 σε αλλη μορφη που δε θα θελει l hospitalΣημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Μάρκος Βασίλης
Πολύ δραστήριο μέλος


Καλησπερα, θεωρειται πως οταν μας δινουνε μια ανισοτικη σχεση για παραδειγμα α^χ>= χ^α και μας λενε να βρουμε το α με φερματ θα πρεπει να γινει και επαληθευση? Δηλαδη αν θεωρησουμε συναρτηση και παρουσιαζει ελαχιστο θα πρεπει να βαλουμε για α την τιμη που θα βρουμε και να δειξουμε οτι παρουσιαζει ελαχιστο?
Αναλόγως πώς είναι διατυπωμένη η άσκηση. Ας δούμε δύο παραδείγματα - δε θα τις λύσουμε, απλώς θα τις σχολιάσουμε.
Παράδειγμα 1: Αν ισχύει ότι


Εδώ κάνεις Fermat και βρίσκεις α=e. Τίποτα παραπέρα.
Παράδειγμα 2: Να βρείτε τις τιμές του α για τις οποίες ισχύει ότι


Εδώ κάνεις Fermat, βρίσκεις α=e και επαληθεύεις μετά με απλή αντικατάσταση και απόδειξη της ανισότητας - εδώ ειδικά, δε χρειάζεται, γιατί η ανισότητα είναι γνωστή.
Ποια είναι όμως η διαφορά ανάμεσα στα δύο παραδείγματα;
Λοιπόν, στο παράδειγμα 1 σου δίνει μία υπόθεση - ότι η f είναι μη αρνητική - και σου λέει να βρεις το α δεδομένης αυτής της υπόθεσης. Με άλλα λόγια, σου ζητάει να βρεις μία αναγκαία συνθήκη έτσι ώστε η f να είναι μη αρνητική, δηλαδή να βρεις ποιες είναι οι τιμές του α στις οποίες πρέπει να περιοριστούμε έτσι ώστε ενδεχομένως να ισχύει η υπόθεση. Άλλωστε, αν παρατηρήσεις την εκφώνηση, δε σου ζητάει πουθενά να αποδείξεις ότι η f είναι μη αρνητική, αλλά να υποθέσεις αυτό (αν...) και να πας παρακάτω για να δείξεις κάτι άλλο.
Στο δεύτερο παράδειγμα, σου ζητάει να βρεις τις τιμές για τις οποίες η υπόθεση είναι αληθής. Με άλλα λόγια, δε σου επιτρέπει να πάρεις την υπόθεση ως δεδομένη όπως στο προηγούμενο παράδειγμα, αλλά σου ζητάει να διερευνήσεις για ποιες τιμές αυτή αληθεύει. Για να το κάνουμε αυτό:
- πρώτα υποθέτουμε ότι η f είναι μη αρνητική, κάνουμε Fermat και βρίσκουμε τις πιθανές τιμές του α - δηλαδή την αναγκαία συνθήκη για να είναι η f μη αρνητική και,
- μετά δείχνουμε ότι αυτή η συνθήκη ήταν ικανή, δηλαδή ότι, πράγματι, για αυτήν την τιμή του α που βρήκαμε η f είναι μη αρνητική.
Παράδειγμα 1: Να δείξετε ότι

Παράδειγμα 2: Να δείξετε ότι

Επομένως, στο πρώτο έχεις να δείξεις μόνο τη μία κατεύθυνση ενώ στο δεύτερο και τις δύο - άρα θες και επαλήθευση.
Οπότε, εξαρτάται το τι πρέπει να κάνεις από το τι σου ζητάει η εκφώνηση.
Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Papachrist
Νεοφερμένο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
eukleidhs1821
Διάσημο μέλος


ευχαριστηση μας φιλε μου να βοηθησουμε αν κατι το ξερουμε!Μακαρι να γραψεις καλα!Τι σχολη στοχευεις?Θα ήθελα να σας ευχαριστήσω όλους για την βοήθεια σας την φετινή περίοδο .....με βοηθήσετε πολύ με διάφορες υποδείξεις ...αναλυτικές επεξηγήσεις και πολλα άλλα.......υπόσχομαι πως μετά τις εξετάσεις θα αρχίσω μια εγώ να βοηθάω μαθητές που ξεκινάνε φέτος την προετοιμασία τους .....καλή συνέχεια ....τα λεμε σύντομα
Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Viedo
Διάσημο μέλος



Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 2 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 232 μέλη διάβασαν αυτό το θέμα:
- Hased Babis
- ChrisG152
- giorgos5002
- giannis06
- Panagiwths12
- mikke
- hristosdab
- trifasikodiavasma
- haji
- thepigod762
- Mariosm.
- soulatso
- oteletampis
- phleidhs
- AggelikiGr
- sir ImPeCaBlE
- veiNqh
- Scandal
- alekos
- Debugging_Demon
- just some guy
- xristosgkm
- ismember
- Apocalypse
- arrow25
- rempelos42
- ggl
- GStef
- QWERTY23
- xrisamikol
- Σωτηρία
- nikoletaz57
- _Aggelos123
- Mariam38
- SlimShady
- strsismos88
- Georgekk
- Lia 2006
- igeorgeoikonomo
- marian
- tsiobieman
- constansn
- Xristosdimitra
- Panagiotis849
- ρενακι 13
- Memetchi
- eukleidhs1821
- Nikkkpat
- Unboxholics
- korlef
- kwstaseL
- Thanos_D
- the purge
- T C
- Giii
- Papachrist
- liaiscool
- Αννα Τσιτα
- globglogabgalab
- Pharmacist01
- otinanai123
- abcdefg12345
- nicole1982
- thecrazycretan
- kvstas92
- KingOfPop
- maria301
- papa2g
- stefan
- Κλημεντίνη
- TonyMontanaEse
- Lathy
- Alexecon1991
- Μάρκος Βασίλης
- Cortes
- το κοριτσι του μαη
- calliope
- ale
- panagiotis G
- Kleanth
- aggelosst9
- BioChemical
- spring day
- nucomer
- Georgia110
- LeoDel
- pink_panther
- Alexandros973
- marsenis
- den antexw allh apotyxia
- KaterinaL
- kiyoshi
- drosos
- Λαμπρινηη
- Bill22
- Chrysablac.
- giorgosp97
- Βλα
- Monster Hunter
- jul25
- xxxtolis
- Stroka
- nicks1999
- totiloz
- Earendil
- mitsakos
- tasost
- lnesb
- ssalex
- alan09
- Livaja10
- χημεια4λαιφ
- Viedo
- UncleJ
- Kostakis45
- Infrared
- Zgian
- pepatogourounaki
- hirasawayui
- GeoCommand
- Eleni54
- American Economist
- EiriniS20
- ΘανάσοςG4
- stamoul1s
- Αριάνα123
- uni77
- Libertus
- tasoss
- PanosCh002
- Unseen skygge
- Νικόλας Ραπ.
- cel123
- The Limit Does Not Exist
- don_vito
- suaimhneas
- Αλκης Κ.
- alexrami
- Baggelitsa36
- Νομικάριος13
- spinalgr1990
- d_th
- Adolfo valencia
- Πα.Κ
- Vasilis25
- Johnman97
- Steffie88
- rekcoR
- gwgw_5
- fockos
- Mariahj
- roud
- kostas83
- Cpt.Philips
- Makis45
- Χρησλου
- Panos_02
- Vold
- tymvorixos
- GiorgosAsi
- Neos167
- theodoraooo
- George187
- Άρτεμις Α.
- Μαρία2222
- christos87
- Idontknoww
- jimis2001
- Metamorph
- Γατόπαρδος.
- Johnsk
- mitsos14
- johnsiak
- Elel
- Dreamer_SW
- Γιαννης1987Θεσσ
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki



