Δίνεται συνάρτηση 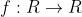 δύο φορές παραγωγίσιμη για την οποία ισχύει
δύο φορές παραγωγίσιμη για την οποία ισχύει  \succ 0) , για κάθε
, για κάθε 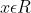 . Να δείξετε ότι η εφαπτομένη της
. Να δείξετε ότι η εφαπτομένη της 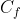 στο σημείο
στο σημείο  \right)) δεν έχει άλλο κοινό σημείο με την
δεν έχει άλλο κοινό σημείο με την 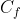 εκτός του
εκτός του 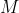
Η εφαπτομένη της Cf στο σημείο (x1,f(x1)) έχει εξίσωση:
y-f(x1)=f΄(x1)(x-x1) <=> y=f΄(x1)x+f(x1)-x1f(x1) <=> y=g(x) όπου g(x)=f΄(x1)x+f(x1)-x1f(x1), x ανήκει R
Θεωρούμε την συνάρτηση h με τύπο h(x)=f(x)-g(x) <=> h(x)=f(x)-f΄(x1)x-f(x1)+x1f(x1), x ανήκει R.
Παρατηρούμε ότι h(x1)=0 <=> f(x1)=g(x1)
Επειδή η f είναι δύο φορές παραγωγίσιμη στο R τότε και η h είναι δύο φορές παραγωγίσιμη στο R με πρώτη και δεύτερη παράγωγο:
h΄(x)=f΄(x)-f΄(x1)
h΄΄(x)=f΄΄(x)
Παρατηρούμε ότι h΄(x1)=0
Επειδή f΄΄(x)>0 για κάθε x ανήκει R τότε h΄΄(x)>0 για κάθε x ανήκει R. Επειδή η h είναι παραγωγίσιμη στο R τότε είναι και συνεχής στο R. Η h είναι συνεχής και δύο φορές παραγωγίσιμη στο R με h΄΄(x)>0 για κάθε x ανήκει R. Επομένως η h είναι κυρτή στο R που σημαίνει ότι η πρώτη παράγωγος h΄ είναι γνησίως αύξουσα στο R. Άρα
x<x1 => h΄(x)<h΄(x1) => h΄(x)<0 για κάθε x ανήκει (-oo,x1)
x>x1 => h΄(x)>h΄(x1) => h΄(x)>0 για κάθε x ανήκει (x1,+oo)
Η h είναι συνεχής στο (-οο,x1], παραγωγίσιμη στο (-οο,x1) και ισχύει h΄(x)<0 για κάθε x ανήκει (-οο,x1). Επομένως η h είναι γνησίως φθίνουσα στο (-οο,x1).
Η h είναι συνεχής στο [x1,+oo), παραγωγίσιμη στο (x1,+oo) και ισχύει h΄(x)>0 για κάθε x ανήκει (x1,+oo). Επομένως η h είναι γνησίως αύξουσα στο (x1,+oo).
x<x1 => h(x)>h(x1) => h(x)>0 για κάθε x ανήκει (-oo,x1)
x>x1 => h(x)>h(x1) => h(x)>0 για κάθε x ανήκει (x1,+oo)
Άρα ισχύει h(x)>0 για κάθε x ανήκει (-oo,x1)U(x1,+oo) και h(x1)=0. Συνεπώς η h παρουσιάζει ολικό ελάχιστο στο x1 και για κάθε x ανήκει (-οο,x1)U(x1,+oo) ισχύει h(x)>0 => h(x) διάφορο 0 που σημαίνει ότι η εφαπτομένη της Cf στο (x1,f(x1)) δεν έχει άλλο κοινό σημείο με την Cf.