Αν για τους μιγαδικούς
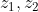
ισχύει
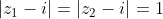
καί
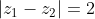
να βρεθεί το
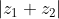
Μια κάπως ανορθόδοξη λύση που μας δίνει περισσότερα στοιχεία από όσα θέλουμε.
Αν z=x+yi όπου x, y ανήκουν R και ισχύει |z-i|=1 τότε έχουμε διαδοχικά |x+(y-1)i|=1 => |x+(y-1)i|^2=1 => (x^2)+(y-1)^2=1
Η παραπάνω εξίσωση παριστάνει κύκλο με κέντρο K(0,1) και ακτίνα ρ=1. Οι παραμετρικές εξισώσεις αυτού του κύκλου είναι x=συνθ, y=1+ημθ όπου 0<=θ<2π
Άρα z1=συνθ1+(1+ημθ1)i, z2=συνθ2+(1+ημθ2)i όπου 0<=θ1<2π και 0<=θ2<2π.
Έχουμε z1-z2=(συνθ1-συνθ2)+(ημθ1-ημθ2)i
Συνεπώς |z1-z2|^2=(συνθ1-συνθ2)^2+(ημθ1-ημθ2)^2=(συνθ1)^2+(συνθ2)^2-2συνθ1συνθ2+(ημθ1)^2+(ημθ2)^2-2ημθ1ημθ2=
=[(ημθ1)^2+(συνθ1)^2]+[(ημθ2)^2+(συνθ2)^2]-2(συνθ1συνθ2+ημθ1ημθ2)=(1+1)-2συν(θ1-θ2)=2-2συν[-(θ2-θ1)]=2[1-συν(θ2-θ1)]>=0 αφού συν(θ2-θ1)<=1
|z1-z2|=2 => |z1-z2|^2=4 => 2(1-συν(θ2-θ1))=4 => 1-συν(θ2-θ1)=2 => συν(θ2-θ1)=-1 => συν(θ2-θ1)=συνπ => θ2-θ1=(2κ+1)π => θ2=θ1+(2κ+1)π, κ ανήκει Ζ
0<=θ1<2π => -2π<-θ1<=0
0<=θ2<2π
Άρα -2π<θ2-θ1<2π => -2π<2κπ+π<2π => -3π<2κπ<π => -(3/2)<κ<(1/2) => κ=-1 ή κ=0
Για κ=-1 είναι θ2=θ1-π
0<=θ2<2π => 0<=θ1-π<2π => π<=θ1

π και επειδή 0<=θ1<2π τότε πρέπει π<=θ1<2π
Αν θ1=θ τότε θ2=θ-π και ημθ2=ημ(θ-π)=-ημ(π-θ)=-ημθ, συνθ2=συν(θ-π)=συν(π-θ)=-συνθ
Για κ=0 είναι θ2=θ1+π
0<=θ2<2π => 0<=θ1+π<2π => -π<=θ1<π και επειδή 0<=θ1<2π τότε πρέπει 0<=θ1<π
Αν θ1=θ τότε θ2=θ+π και ημθ2=ημ(θ+π)=ημ(π-(-θ))=ημ(-θ)=-ημθ, συνθ2=συν(θ+π)=συν(π-(-θ))=-συν(-θ)=-συνθ
Και στις 2 περιπτώσεις είναι ημθ2=-ημθ, συνθ2=-συνθ
Συνεπώς z1=συνθ1+(1+ημθ1)i=συνθ+(1+ημθ)i, z2=συνθ2+(1+ημθ2)i=-συνθ+(1-ημθ)i όπου 0<=θ<2π
Έχουμε z1+z2=2i. Άρα |z1+z2|=|2i|=|2||i|=2*1=2