Θεωρώ
={x}^{3}-6{x}^{2}+12x)
. Η g είναι συνεχής και παραγωγίσιμη στο R ως πολυωνυμική με παράγωγο:
=3{x}^{2}-12x+12=3\left({x}^{2}-4x+4 \right)=4\left{(x-2 \right)}^{2})
, x ανήκει R
g συνεχής στο
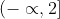
, παραγωγίσιμη στο
)
και g'(x)>0 για κάθε
)
. Άρα η g είναι γνησίως αύξουσα στο
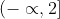
.
g συνεχής στο
)
, παραγωγίσιμη στο
)
και g'(x)>0 για κάθε
)
. Άρα η g είναι γνησίως αύξουσα στο
)
.
Επομένως η g είναι γνησίως αύξουσα στο R. Άρα είναι 1-1 και συνεπώς αντιστρέψιμη.
=+\propto )
και
=-\propto )
Το πεδίο ορισμού της g είναι
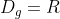
. Επειδή η f είναι συνεχής και γνησίως αύξουσα στο R, το πεδίο τιμών της είναι
=\left(\lim_{x\rightarrow -\propto }g(x),\lim_{x\rightarrow +\propto }g(x) \right)=(-\propto ,+\propto )=R)
Η f έχει πεδίο ορισμού
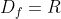
. Θεωρώ
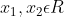
με
=f({x}_{2}))
=f({x}_{2})\Rightarrow {\left( f({x}_{1})\right)}^{3}={\left( f({x}_{2})\right)}^{3})
=f({x}_{2})\Rightarrow {\left( f({x}_{1})\right)}^{2}={\left( f({x}_{2})\right)}^{2}\Rightarrow -6{\left( f({x}_{1})\right)}^{2}=-6{\left( f({x}_{2})\right)}^{2})
=f({x}_{2})\Rightarrow 12f({x}_{1})=12f({x}_{2}))
Άρα
\right)}^{3}-6{\left( f({x}_{1})\right)}^{2}+12f({x}_{1})={\left( f({x}_{2})\right)}^{3}-6{\left( f({x}_{2})\right)}^{2}+12f({x}_{2})\Rightarrow {x}_{1}={x}_{2})
Επομένως για κάθε
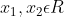
ισχύει η συνεπαγωγή:
=f({x}_{2})\Rightarrow {x}_{1}={x}_{2})
οπότε η f είναι 1-1 και συνεπώς αντιστρέψιμη. Ισχύει
\Leftrightarrow x={f}^{-1}(y))
για κάθε
)
Επομένως
={y}^{3}-6y+12y\Rightarrow {f}^{-1}(y)=g(y))
Είναι
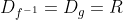
και
=g\left( {D}_{g}\right)=R)
Άρα
={D}_{{f}^{-1}}=R)
={D}_{{f}^{-1}}=R)
Στην δοσμένη σχέση τίθεται x=0:
\right)}^{3}-6{\left( f(0)\right)}^{2}+12f(0)=0\Rightarrow f(0)\left[{\left( f(0)\right)}^{2}-6f(0)+12 \right]=0)
Θεωρώ το πολυώνυμο
={x}^{2}-6x+12)
. Θα εξεταστεί το πρόσημο του P(x) για τις διάφορες τιμές του
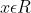
.
}^{2}-4{}^{.}1{}^{.}12=36-48=-12<0)
. Άρα P(x)>0 για κάθε
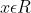
.
Συνεπώς f(0)=0 <=> (f-1)(0)=0.
Στη συνέχεια θα γίνει εφαρμογή της εξής πρότασης της οποίας η απόδειξη είναι πολύ απλή και αφήνεται ως άσκηση: "Αν μία συνάρτηση f είναι 1-1 και η αντίστροφή της είναι παραγωγίσιμη στο
)
και ισχύει
'(f({x}_{0}))\neq 0)
τότε η f είναι παραγωγίσιμη στο
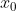
και ισχύει
\neq 0)
"
Επειδή η
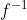
είναι παραγωγίσιμη στο
=R)
και για κάθε
\bigcup (2,+\propto ))
ισχύει
'(y)\neq 0)
, έπεται ότι η f είναι παραγωγίσιμη στο
\bigcup (2,+\propto ))
και ισχύει
\neq 0)
για κάθε
\bigcup (2,+\propto ))
ενώ η f δεν είναι παραγωγίσιμη στο 2 γιατί (f-1)'(2)=0.
Αποδεικνύεται ότι
'(f(x))=\frac{1}{f'(x)})
'(f(x))=\frac{1}{f'(x)}\Rightarrow ({f}^{-1})'(f(x))f'(x)=1\Rightarrow 3{\left(f(x)-2) \right}^{2}f'(x)=1\Rightarrow 3{\left(f(x)-2) \right}^{2}f'(x)-1=0)
για κάθε
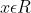
Θεωρώ την συνάρτηση
={\left(f(x)-2 \right)}^{3}-x)
. Επειδή η f είναι παραγωγίσιμη στο R τότε είναι και συνεχής στο R. Επειδή η f είναι συνεχής και παραγωγίσιμη στο R τότε και η h είναι συνεχής και παραγωγίσιμη στο R με παράγωγο
=3{\left(f(x)-2 \right)}^{2}f'(x)-1\Rightarrow h'(x)=0)
Η h είναι συνεχής και παραγωγίσιμη στο R και ισχύει
=0)
για κάθε
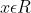
. Άρα η h είναι σταθερη, οπότε
=c)
για κάθε
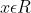
.
={\left(f(0)-2 \right)}^{3}-0={(0-2)}^{3}={(-2)}^{3}=-8\Rightarrow c=h(0)=-8)
Άρα
=-8)
για κάθε
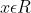
.
=-8\Rightarrow {\left(f(x)-2 \right)}^{3}-x=-8\Rightarrow {\left(f(x)-2 \right)}^{3}=x-8\Rightarrow)
για κάθε
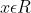
.
Αν
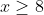
, τότε
-2=\sqrt[3]{x-8}\Rightarrow f(x)=2+\sqrt[3]{x-8})
.
Αν
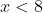
, τότε
-2=-\sqrt[3]{8-x}\Rightarrow f(x)=2-\sqrt[3]{8-x})
.
-----------------------------------------
thanks lostG

. Το έμαθα πολύ καλά με λίγη εξάσκηση. Πριν 15 μέρες δεν ήξερα καν τι είναι.