Μια συμπαθητική που θυμάμαι:
Έστω
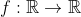
συνεχής και αύξουσα. Να δειχθεί οτι υπάρχει μοναδικό
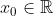
τέτοιο ώστε
=-x_0)
Υπόδειξη:
\geq f(0))
Κάτι με Bolzano παίζει αλλά το θέμα είναι πως βρίσκεις το διάστημα. Άντε και πολλά είπα

Η συνάρτηση f είναι αύξουσα στο R, οπότε για κάθε x1, x2 στο R με x1<x2 ισχύει f(x1)<=f(x2).
Θεωρώ την συνάρτηση g(x)=f(x)+x. Η g είναι συνεχής στο R ως άθροισμα συνεχών στο R συναρτήσεων.
Για κάθε x1, x2 στο R με x1<x2 ισχύει f(x1)<=f(x2). Προσθέτοντας κατά μέλη τις 2 τελευταίες ανισότητες προκύπτει f(x1)+x1<f(x2)+x2 => g(x1)<g(x2).
Άρα για κάθε x1, x2 στο R με x1<x2 ισχύει g(x1)<g(x2). Επομένως η συνάρτηση g είναι γνησίως αύξουσα στο R και συνεπώς είναι 1-1.
Η f είναι συνεχής στο R. Συνεπώς σύμφωνα με το θεώρημα μέγιστης-ελάχιστης τιμής συνεχών συναρτήσεων, για κάθε x στο R υπάρχουν m, M στο R τέτοιοι ώστε m<=f(x)<=M για κάθε x στο R.
m<=f(x)<=M => m+x<=f(x)+x<=M+x => m+x<=g(x)<=M+x για κάθε x στο R.
lim(x->-άπειρο)(m+x)=lim(x->-άπειρο)(M+x)=-άπειρο
Σύμφωνα με το κριτήριο παρεμβολής είναι lim(x->-άπειρο)g(x)=-άπειρο.
Από τον ορισμό του ορίου προκύπτει ότι υπάρχει α<0 ώστε για κάθε x στο (-άπειρο, α) να υπάρχει m΄<0 τέτοιο ώστε g(x)<m΄ για κάθε x στο (-άπειρο, α). Επειδή g(x)<m΄ και m΄<0 τότε g(x)<0 για κάθε x στο (-άπειρο, α). Άρα υπάρχει χ1 στο (-άπειρο,α) τέτοιο ώστε g(x1)<0.
lim(x->+άπειρο)(m+x)=lim(x->+άπειρο)(M+x)=+άπειρο
Σύμφωνα με το κριτήριο παρεμβολής είναι lim(x->+άπειρο)g(x)=+άπειρο.
Από τον ορισμό του ορίου προκύπτει ότι υπάρχει β>0 ώστε για κάθε x στο (β, +άπειρο) να υπάρχει M΄>0 τέτοιο ώστε g(x)>M΄ για κάθε x στο (β, +άπειρο). Επειδή g(x)>M΄ και Μ΄>0 τότε g(x)>0 για κάθε x στο (β, +άπειρο). Άρα υπάρχει χ2 στο (β, +άπειρο) τέτοιο ώστε g(x2)>0.
Η συνάρτηση g είναι συνεχής στο [x1, x2] και ισχύει g(x1)g(x2)<0. Σύμφωνα με το θεώρημα Bolzano υπάρχει τουλάχιστον ένα x0 στο (x1, x2) τέτοιο ώστε g(x0)=0.
Επειδή η g είναι 1-1, τότε υπάρχει μοναδικό x0 τέτοιο ώστε g(x0)=0 => f(x0)=-x0