Φρεντος
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Διονύσης13
Τιμώμενο Μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Filippos14
Εκκολαπτόμενο μέλος


Γεια σας παιδια θα ηθελα να ρωτησω τι συμβαινει ακριβως με τις φορες για καποιο λογο οταν λυνω ασκησεις εχει τυχει πολλες φορες να βαλω ως θετικη φορα αυτη που ειναι αντιθετη με την φορα περιστροφης των δεικτων του ρολογιου και τα αποτελεσματα οταν εφαρμοζω Στ=ΙR και ΣF=ma
να βγαινουν οπως ναναι με ποιο τροπο γινεται να βρισκω παντα ποια φορα πρεπει να θεωρησω ως σωστη;
Ισως σου φανει λιγο χαζο αυτο που κανω αλλα εμενα με βοηθαει.Συνηθως βαζω οποια φορα μου φενετε καλη στο ματι,και για τα προσημα κανω το εξης:
Φανταζομαι οτι στον αξονα περιστροφης εχουμε καρφωσει ενα καρφι που κραταει το σωμα και απλα φανταζομαι οτι πχ αν του ασκησω μια δυναμη στο cm του προσ τα που τηνει να παει το σωμα.
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


και αν εφαρμοζεις τους νομους αυτους για να βρεις προς τα που θα κινηθει η θα περιστραφει το σωμα τοτε πως θα ξερεις ποιες φορες να παρεις ως θετικες ;Βαζε στη μεταφορικη θετικες αυτες που ειναι στη φορα της κινησης σου και στη στροφικη αυτες που δινουν ροπη που "ευνοει" τη στροφη της κινησης σου. (πως το ειπα ετσι; :p)
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Filippos14
Εκκολαπτόμενο μέλος


Τι εννοεις οτι οι δυναμεις βγαινουν οτι ναναι,γινε λιγο πιο συγκεκριμενος γιατι δεν καταλαβα τι εννοεις ακριβως.Εισαι αριστεροχειρας?Μα δεν μου βγαινουν απλα αντιθετοι οι αριθμοι μου βγαινουν οπως ναναι οι δυναμεις... για ποιο λογο γινεται αυτο ;
και αν εφαρμοζεις τους νομους αυτους για να βρεις προς τα που θα κινηθει η θα περιστραφει το σωμα τοτε πως θα ξερεις ποιες φορες να παρεις ως θετικες ;
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Dias
Επιφανές μέλος


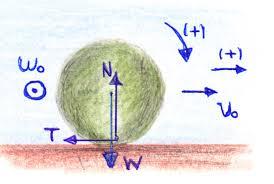
Το ποια φορά θα θεωρήσουμε θετική είναι (γενικά) αυθαίρετο. Όμως, υπάρχει μια λεπτομέρεια που μπορεί να οδηγήσει σε λάθος αποτελέσματα. Σε μια κύλιση χωρίς ολίσθηση, οι θετικές φορές που θα ορίσουμε για τη μεταφορική και τη στροφική κίνηση, δεν πρέπει να είναι και οι δύο αυθαίρετες, αλλά πρέπει να είναι συμβατές, δηλαδή να δίνουν το ίδιο πρόσημο (πιο καλά θετικό) μεταφορικής (CM) και γωνιακής επιτάχυνσης.Μα δεν μου βγαινουν απλα αντιθετοι οι αριθμοι μου βγαινουν οπως ναναι οι δυναμεις... για ποιο λογο γινεται αυτο ;
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Guest 018946
Επισκέπτης


Το ποια φορά θα θεωρήσουμε θετική είναι (γενικά) αυθαίρετο. Όμως, υπάρχει μια λεπτομέρεια που μπορεί να οδηγήσει σε λάθος αποτελέσματα. Σε μια κύλιση χωρίς ολίσθηση, οι θετικές φορές που θα ορίσουμε για τη μεταφορική και τη στροφική κίνηση, δεν πρέπει να είναι και οι δύο αυθαίρετες, αλλά πρέπει να είναι συμβατές, δηλαδή να δίνουν το ίδιο πρόσημο (πιο καλά θετικό) μεταφορικής (CM) και γωνιακής επιτάχυνσης.

Σωστός ο πιτσιρίκος .
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
DumeNuke
Τιμώμενο Μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
liakosttpψ
Νεοφερμένο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
gersi
Εκκολαπτόμενο μέλος


Χωρις να ειμαι απολυτα σιγουρος. Για την ασκηση με την σφαιρα θα χρησιμοποιησεις ενεργειες. Στην πρωτη περιπτωση κανει ολισθηση(λειο εδαφος) αρα δεν υπαρχουν τριβες. Αντιθετα στην δευτερη κανει Κ.Χ.Ο. (τραχυ εδαφος) αρα υπαρχουν τριβες. Η τριβη στην δευτερη περιπτωση δινει και ροπη. Σε αντιθεση με την πρωτη περιπτωση οπου εχεις μονο μεταφορικη κινηση. Πρεπει να δειξεις οτι χανεται ενεργεια λογω της τριβης στην δευτερη περιπτωση. Για αυτο και ισχυει η σχεση Ucm1>Ucm2.θα ηθελα επισης και μια ακομα βοηθεια σε αυτες εδω
Θα τις κοιταξω και τις δυο το βραδυ τωρα δεν προλαβαινω να τις δω οπως θελω.
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


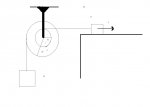
Παιδια γεια ελπιζω το σχημα να μην βγει οπως ναναι
λοιπον
Η διπλη τροχαλια του σχηματος αποτελειται απο δυο κολλημενους μεταξυ τους δισκους (1) και (2) που εχουν κοινο κεντρο Κ
μαζες Μ1=5kg και M2=8kg και ακτινες R1=0,4m Και R2=0,5m αντιστοιχα. Η διπλη τροχαλια μπορει να περιστρεφεται χωρις τριβες ως ενα σωμα γυρω απο οριζοντιο ακλονητο αξονα που διερχεται απο το κοινο κεντρο Κ των δυο δισκων και ειναι καθετος στο επιπεδο τους. Σε καθε δισκο εχουμε τυλιξει σε πολλες στροφες αβαρες και μη εκτατο νημα και στα ελευθερα ακρα των νηματων εχουμε δεσει τα μικρα σωματα Σ1 και Σ2 με μαζες m1=2,5 kg και m2=4kg οπως φαινεται στο σχημα Απο τη χρονικη στιγμη t=0 και μετα ασκουμε στο σωμα Σ1 οριζοντια σταθερη δυναμη F οποτε αυτο αρχιζει να κινειτα προς τα δεξια με σταθερη επιταχυνση α1 μετρου 4m/s^2 ενω η τροχαλια αρχιζει να περιστρεφεται. Το δαπεδο πανω στο οποιο κινειται το σωμα Σ1 ειναι λειο η αντισταση του αερα αμελητεα και τα νηματα δε γλιστρουν στα αυλακια των δυο δισκων. Να υπολογισετε: α)το μετρο της γωνιακης επιταχυνσης της τροχαλιας καθως και το μετρο της επιταχυνσης του σωματος Σ2
β)Τον αριθμο των περιστροφων που εχει εκτελεσει η τροχαλια απο τη χρονικη στιγμη t=0 εως τη χρονικη στιγμη t1 που το σωμα Σ1 απεκτησε ταχυτητα μετρου u1=8m/s
γ) το μετρο της δυναμης F
τα δυο πρωτα ερωτηματα τα ξερω αλλα θελω να σταθω στο 3ο δοκιμασα να θεωρησω ως φορα της μεταφορικης κινησης αντιθετη απο αυτη της λυσης στον αξονα των χ(σωμα Σ1) ΜΟΝΟ
και μετα εφαρμοσα Στ=Iαγων και ΣFx=mα1 και ΣFy=mα2
και τελικα το αποτελεσμα ηταν διαφορετικο απο αυτο του βιβλιου μετα αλλαξα την φορα και στο ΣFx και στο ΣFy και Στο Στ=Ιαγων
μετα πηρα αντιθετες φορες και στον αξονα τον χ και y καθως και στην περιστροφικη κινηση και τα αποτελεσματα βγηκαν οπως του βιβιλιου. Μετα πηρα αντιθετη φορα μονο στην περιστροφικη κινηση και κρατησα τα υπολοιπα ιδια.
Τα διαφορετικα αποτελεσματα που οφειλονται;;;
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Dias
Επιφανές μέλος


Δεν υπάρχει κανένας λόγος να παίζεις με τις φορές. Παίρνεις θετικές τις φορές που βγάζουν θετικές επιταχύνσεις. (Για το Σ1 δεξιά, για το Σ2 επάνω, για την τροχαλία αυτή των δεικτών του ρολογιού). Έτσι δεν κινδυνεύεις να κάνεις λάθος. Διάβασε ΕΔΩ τι έγραψα μερικά μηνύματα πιο πριν. Τα διαφορετικά αποτελέσματα οφείλονται (μάλλον) στο ότι άλλαξες τη θετική φορά, πήρες σωστά τις δυνάμεις, αλλά δεν άλλαξες πρόσημα στις επιταχύνσεις. Δεν έχουν νόημα τα ...πειράματά σου, άδικα χάνεις το χρόνο σου.......δοκιμασα να θεωρησω ως φορα της μεταφορικης κινησης αντιθετη απο αυτη της λυσης στον αξονα των χ(σωμα Σ1) ΜΟΝΟ ..... μετα αλλαξα την φορα ....... μετα πηρα αντιθετες φορες και στον αξονα τον χ και y καθως και στην περιστροφικη κινηση ........ Μετα πηρα αντιθετη φορα μονο στην περιστροφικη κινηση και κρατησα τα υπολοιπα ιδια. Τα διαφορετικα αποτελεσματα που οφειλονται;;;
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


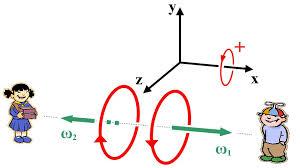
Σώμα είναι δεμένο σε ελατήριο σταθεράς k και εκτελεί κύλιση χωρίς ολίσθηση
Να αποδείξετε ότι εκτελεί ΑΑΤ με T=2π*ρίζα(2m/3k)
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
gersi
Εκκολαπτόμενο μέλος


- στην ραβδο με αρθρωση;
- στην ακινητη τροχαλια; (οταν ειναι καπου στερεωμενη π.χ. εδαφος,οροφη)

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Dias
Επιφανές μέλος


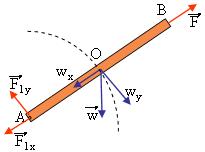
Τη σχεδιάζεις όπως σε καθοδηγεί το ενστικτό σου, δηλαδή στην τύχη. Βρίσκεις συνιστώσες Fx, Fy και από τα πρόσημά τους καταλαβαίνεις αν μάντεψες σωστά ή ανάποδα.Ξεκινησα επαναληψη απο την Παρασκευη και αντιμετωπιζω ενα προβλημα στις ροπες. Συγκεκριμενα με την Fαξονα. Πως θα καταλαβω προς τα που θα την σχεδιασω; Μια μεθοδολογια για τον σχεδιασμο αυτων των δυναμεων θα ηταν σωτηρια.
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


Ξεκινησα επαναληψη απο την Παρασκευη και αντιμετωπιζω ενα προβλημα στις ροπες. Συγκεκριμενα με την Fαξονα. Πως θα καταλαβω προς τα που θα την σχεδιασω:
- στην ραβδο με αρθρωση;
Μια μεθοδολογια για τον σχεδιασμο αυτων των δυναμεων θα ηταν σωτηρια.
- στην ακινητη τροχαλια; (οταν ειναι καπου στερεωμενη π.χ. εδαφος,οροφη)
Από όσο ξέρω, την F στην άρθρωση την βάζεις κατάλληλα ώστε οι δυνάμεις που ασκούνται να έχουν ένα κοινό σημείο αν τις προεκτείνεις. Κάπως έτσι θυμάμαι ότι το έκανα αλλά δεν θυμάμαι την αιτιολόγηση. Θα το ψάξω να το βρω και θα απαντήσω πάλι. Βέβαια δεν ξέρω αν αυτό που λέω είναι τελείως λάθος αλλά εγώ έτσι έβρισκα πως να βάλω την F
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Dias
Επιφανές μέλος


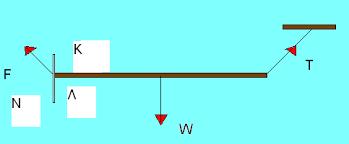
Αυτό είναι το λεγόμενο "θεώρημα των 3 δυνάμεων σε ισορροπία". Όμως:Από όσο ξέρω, την F στην άρθρωση την βάζεις κατάλληλα ώστε οι δυνάμεις που ασκούνται να έχουν ένα κοινό σημείο αν τις προεκτείνεις.
α) Ισχύει μόνον αν οι δυνάμεις είναι τρεις (3).
β) Δίνει τη διεύθυνση αλλά όχι πάντα και τη φορά της άγνωστης δυναμης.
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Guest 018946
Επισκέπτης


Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


Ένας κύβος μάζας m=10kg ισορροπεί τοποθετημένος πάνω σε λείο οριζόντιο
επίπεδο. Στη μια κατακόρυφη έδρα του κύβου είναι δεμένη η μια άκρη ιδανικού οριζόντιου
ελατηρίου σταθεράς k=250N/m , του οποίου η άλλη άκρη είναι δεμένη σε
ακλόνητο σημείο κατακόρυφου τοίχου. Το ελατήριο βρίσκεται στο φυσικό του μήκος. Στην
απέναντι κατακόρυφη έδρα του κύβου είναι δεμένο μη ελαστικό και αβαρές νήμα το οποίο
έχει όριο θραύσεως F (θραύσεως)=120Ν
.
Μέσω του νήματος ασκούμε στο σώμα δύναμη κατά τη διεύθυνση του άξονα του
ελατηρίου και με φορά τέτοια ώστε το ελατήριο να επιμηκύνεται. Το μέτρο της δύναμης
μεταβάλλεται σε συνάρτηση με την επιμήκυνση x του ελατηρίου σύμφωνα με την εξίσωση F=80+200x
(SI).
α) Να βρείτε τη δυναμική ενέργεια του ελατηρίου τη στιγμή που κόβεται το νήμα.
β) Να βρείτε την ταχύτητα του κύβου τη στιγμή που κόβεται το νήμα.
γ) Να γράψετε την εξίσωση της απομάκρυνσης y=f(t) . Να θεωρήσετε t=0 τη
στιγμή που κόβεται το νήμα και άξονα x'x με αρχή τη θέση ισορροπίας του κύβου και
θετική φορά εκείνη κατά την οποία το ελατήριο επιμηκύνεται.
δ) Να βρείτε μετά από πόσο χρόνο από τη στιγμή που κόβεται το νήμα, θα
περάσει ο κύβος από τη θέση ισορροπίας του για πρώτη φορά.
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Dias
Επιφανές μέλος


Xe! Την άσκηση αυτή την είχαμε λύσει στο θέμα "επιλεγμένα προβλήματα φυσικής" το 2010 που ήμουν υποψήφιος.μπορεί κάποιος να με βοηθήσει με αυτη την ασκηση?Ένας κύβος μάζας m=10kg ισορροπεί τοποθετημένος πάνω σε λείο οριζόντιο
επίπεδο. Στη μια κατακόρυφη έδρα του κύβου είναι δεμένη η μια άκρη ιδανικού οριζόντιου
ελατηρίου σταθεράς k=250N/m , του οποίου η άλλη άκρη είναι δεμένη σε
ακλόνητο σημείο κατακόρυφου τοίχου. Το ελατήριο βρίσκεται στο φυσικό του μήκος. Στην
απέναντι κατακόρυφη έδρα του κύβου είναι δεμένο μη ελαστικό και αβαρές νήμα το οποίο
έχει όριο θραύσεως F (θραύσεως)=120Ν
Μέσω του νήματος ασκούμε στο σώμα δύναμη κατά τη διεύθυνση του άξονα του
ελατηρίου και με φορά τέτοια ώστε το ελατήριο να επιμηκύνεται. Το μέτρο της δύναμης
μεταβάλλεται σε συνάρτηση με την επιμήκυνση x του ελατηρίου σύμφωνα με την εξίσωση F=80+200x (SI).
α) Να βρείτε τη δυναμική ενέργεια του ελατηρίου τη στιγμή που κόβεται το νήμα.
β) Να βρείτε την ταχύτητα του κύβου τη στιγμή που κόβεται το νήμα.
γ) Να γράψετε την εξίσωση της απομάκρυνσης y=f(t) . Να θεωρήσετε t=0 τη
στιγμή που κόβεται το νήμα και άξονα x'x με αρχή τη θέση ισορροπίας του κύβου και
θετική φορά εκείνη κατά την οποία το ελατήριο επιμηκύνεται.
δ) Να βρείτε μετά από πόσο χρόνο από τη στιγμή που κόβεται το νήμα, θα
περάσει ο κύβος από τη θέση ισορροπίας του για πρώτη φορά.
Στην επικολλώ κι εδώ:
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 1 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 312 μέλη διάβασαν αυτό το θέμα:
- eftria
- Magigi
- Chrisphys
- BillyTheKid
- ck_chrysiis
- trifasikodiavasma
- GV221
- nearos
- myrtle09
- Reader
- Unboxholics
- Μήτσος10
- jellojina
- Hased Babis
- Joji
- Corfu kitty
- Maynard
- BatGuin
- KonstantinosP
- jYanniss
- exotic xo
- Qwerty 0
- userguest
- ioanna2007
- suaimhneas
- Debugging_Demon
- panosT436
- bibliofagos
- Scandal
- bboys
- georgetherrr
- Ness
- sophiaa
- mir
- Than003
- Vasilis125
- pnf292
- synthnightingale
- sakplat
- iiTzArismaltor_
- thepigod762
- Nala
- Γατέχων
- vasilis2000
- peter347
- Sofos Gerontas
- chester20080
- Greg25
- woasibe
- angela_k
- BiteTheDust
- Startx0
- MR WHITE
- Panatha mono
- bill09876
- Wonderkid
- Marel
- Chris180
- Claire05
- TheNorth
- estrela
- Marianna.diamanti
- love_to_learn
- carnage
- sotirislk
- ένας τυχαίος
- Lifelong Learner
- Jimpower
- Kate1914
- phleidhs
- Chemwizard
- Mara2004
- GeorgeKarag
- phoni
- Mary06
- Lia 2006
- Νομάρχης
- Γιώτα Γιαννακού
- PanosApo
- Ilovemycats27
- Jesse_
- Leo komm
- Anonymous1
- giannis256
- spring day
- Mewmaw
- Mariamar
- Pharmacist01
- Kitana
- Vicky13
- mitskification
- ΜΑΡΙΠΟΖΑ
- denjerwtithelwhelp
- Abiogenesis
- arko
- arapakos
- Marcos.Kis
- Nick_nt
- Alexecon1991
- Physicsstudent
- anna05
- katia.m
- Deneimaikala
- shezza94
- Fanimaid123
- το κοριτσι του μαη
- user-2
- tsiobieman
- Alex53
- Helen06
- T C
- eukleidhs1821
- VFD59
- xrisamikol
- lepipini
- ioanna06
- PanosBat
- rempelos42
- koukdespoina2004
- Antzie
- george777
- User2350
- qwertyuiop
- marioushi
- Nic Papalitsas
- menual
- oups
- Applepie
- eirinipap
- Jojo K
- ggl
- margik
- desp1naa
- walterrwhite
- JoannaVas
- ismember
- P.Dam.
- Χάρις
- penelopenick
- rosemary
- Steliosgkougkou
- the purge
- AnnaRd
- Signor Positivo
- onion
- cinnamongirl
- mister
- thenutritionist
- angies
- sophia<3
- Peter Pan13
- angeloskar
- Georgek7
- tapeinoxamomilaki
- Ιωάννης1234
- Praxis
- Mariahj
- Τρελας123
- Sherlockina
- Παναρας
- DimitrisGk
- Ελεν
- giannhs2001
- Idontknoww
- anakiriak@yahoo
- mpapa
- BlackBetty97
- ager
- kost28
- Eirinakiii8
- Cat lady
- Marple
- χημεια4λαιφ
- Apocalypse
- Valeris
- Vask
- Ioanna98
- ougka pougka
- GeorgePap2003
- Johanna Mark
- bruh_234
- augustine
- alpha.kappa
- Hermione granger
- constansn
- emilyfan85
- 2005
- George.S
- Dion G.
- SlimShady
- Corn90
- Meow
- Phys39
- Nick0007
- Nikoletaant
- Ameliak
- beckyy
- Rina
- Lathy
- Eleni:
- Specon
- elenaaa
- Αντικειμενικός
- Mariaathens
- panosveki
- Superhuman
- GStef
- Gewrgia!
- papa2g
- Σωτηρία
- antonis97
- Georgekk
- Theodora03
- vetas
- _Aggelos123
- Κώστας 7708
- Alexandros973
- Cortes
- Katerinaki13
- Jimmy20
- igeorgeoikonomo
- KaterinaL
- thecrazycretan
- alexandra_
- StavMed
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki


