Η ΗΕΔ από αυτεπαγωγή δεν 'ναι τίποτα σπουδαίο. Όπως ξέρουμε, ισούται με:
}{dt})
Προσοχή, χωρίς το (-), όπως ήταν ο τύπος της Β' Λυκείου.
Δηλαδή είναι η τάση στα άκρα του πηνίου.
Κι από δω και πέρα έχουμε 2 τρόπους να το βρούμε συναρτήσει του t. Ο πρώτος αντικαθιστούμε το i στην έκφραση - δηλαδή το παραγωγίζουμε πρώτα ως προς τον χρόνο (μισή γραμμή για όσους ξέρουν από τώρα παραγώγους) και το αντικαθιστούμε.
Γενικά να ξέρετε πως παράγωγοι (κι ολοκληρώματα πιστεύω, αλλά παράγωγοι στάνταρ) είναι εντελώς αποδεκτοί σε μία άσκηση (καθώς στο τέλος των θεμάτων σημειώνεται πως οποιαδήποτε επιστημονικά τεκμηριωμένη απάντηση είναι αποδεκτή).
Ο δεύτερος τρόπος εφαρμόζοντας τον 2ο νόμο του Kirchhoff στο κύκλωμα, παίρνουμε:
}{C}<br />
\end{eqnarray}<br />
)
Οπότε αντικαθιστώντας την q(t) έχεις την ΗΕΔ από επαγωγή.
------------------------------
Δείτε και κάτι άλλο ενδιαφέρον πάνω σ' αυτό.
2ος νόμος του Kirchhoff στο κύκλωμα:
}{dt} + \frac{q(t)}{C} & = & 0 \\<br />
\frac{di(t)}{dt} + \frac{q(t)}{LC} & = & 0 \\<br />
\frac{d^2q(t)}{dt^2} + \frac{q(t)}{LC} & = & 0 \\<br />
q''(t) + \frac{q(t)}{LC} & = & 0 \\<br />
\end{eqnarray}<br />
)
Αυτή είναι η
διαφορική εξίσωση του κυκλώματος, την οποία φυσικά δεν είναι απαραίτητο να ξέρετε να την λύσετε και δεν θα κληθείτε να επιλύσετε ποτέ μία διαφορική εξίσωση στη φυσική (στα μαθηματικά μπορεί και ναι).
Εντούτοις αυτή η εξίσωση μπορεί να σας βοηθήσει να λύσετε ερωτήματα όπως "Ποιος είναι ο ρυθμός μεταβολής του ρυθμού μεταβολής του φορτίου q(t) συναρτήσει του χρόνου;". Μία "ψαρωτική" εκφώνηση, που απλά ζητάει το μέγεθος
}{dt^2})
.
Που μπορεί να βρεθεί φυσικά και παραγωγίζοντας 2 φορές την
)
.
Ή μπορεί να μην σας ζητηθεί ως "ρυθμός μεταβολής του ρυθμού μεταβολής του φορτίου" αλλά πιο συνηθισμένα ως "ρυθμός μεταβολής του ρεύματος", που το 'χω πετύχει αρκετές φορές. Από τα παραπάνω έπεται:
}{dt} = - \frac{q(t)}{LC})
Ή πιο απλά υπολογίζεται παραγωγίζοντας το ρεύμα i(t) μια φορά ως προς το χρόνο.
Εδώ να θυμήσω κάποια βασικά πράγματα.
- Το ότι
 = \frac{dq(t)}{dt} = q'(t))
(παράγωγος) είναι ο ορισμός του ρεύματος. Δηλαδή είναι ο ρυθμός μεταβολής του φορτίου q ως προς το χρόνο. Δηλαδή, όσοι ξέρετε παραγώγους, παραγωγίζετε την q(t) ως προς το χρόνο και voila, το ρεύμα i(t) [απόλυτα αποδεκτό, δεν υπάρχει φυσικός που δεν το ξέρει αυτό].
- Το είναι η δεύτερη παράγωγος του q(t) ως προς το χρόνο και γράφεται κι ως
}{dt^2} = \frac{d}{dt}\left ( \frac{dq(t)}{dt} \right ) = \frac{di(t)}{dt})
.
------------------------------
Τα παρακάτω δεν είναι απαραίτητα, αλλά τα παραθέτω για επιστημονικό ενδιαφέρον.
Διαφορική εξίσωση είναι μία "εξίσωση" όπου ζητείται μία συνάρτηση ως προς ένα μέγεθος και "εμπλέκονται" μες στη εξίσωση παράγωγοι αυτού του μεγέθους. Για παράδειγμα, η διαφορική εξίσωση που προκύπτει είναι η:
}{dt^2} + \frac{q(t)}{LC} = 0)
Όπου η άγνωστη συνάρτηση είναι η
και μέσα στη συνάρτηση "εμπλέκεται" και μία παράγωγός της, που είναι δεύτερης τάξης (η παράγωγος της παραγώγου της).
Ποια είναι η λύση της διαφορικής; Μα φυσικά αυτή:
 = Q_0sin(\frac{1}{sqrt{LC}}t + \phi_0))
(Δοκιμάστε κιόλας να δείτε ότι επαληθεύει την διαφορική) Όπου θέτουμε
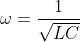
(να λοιπόν πώς προκύπτει η γωνιακή συχνότητα). Επίσης τα
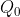
και
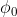
είναι οι δύο αρχικές συνθήκες που θα δίνονται. Μάλιστα, οι αρχικές συνθήκες είναι δύο (2) επειδή η μεγαλύτερη σε τάξη παράγωγος στην εξίσωση είναι δευτέρου βαθμού. Στο παράδειγμα του βιβλίου το
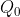
θεωρείται γνωστό (μία θετική σταθερά) και η αρχική φάση
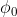
θεωρείται ίση με
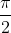
. Κι έτσι έχουμε την γνωστή εξίσωση:
 = Q_0sin(\omega t + \frac{\pi}{2}) \\<br />
q(t) = Q_0cos(\omega t))
Και με παραγώγιση:
 = -\omega Q_0sin(\omega t) \\<br />
i(t) = -I_0sin(\omega t), \;\; \text{\mu\epsilon} \: I_0=\omega\cdot Q_0)
Άρα, το "γιατί" ο πυκνωτής εκφορτίζεται κι επαναφορτίζεται με αντίθετη πολικότητα και ξανά μανά, εξηγείται απλά: έτσι προκύπτει από την επίλυση της διαφορικής.
Αργότερα στα μαθηματικά κατεύθυνσης θα μάθετε (απλά δεν θα το ονομάζετε "επίλυση διαφορικής") να λύνετε διαφορικές εξισώσεις πρώτου βαθμού χωρισμένων μεταβλητών, δηλαδή της μορφής:
}{dx} + b\cdot y(x) = c)
