Έστω
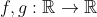
για τις οποίες για κάθε

ισχύουν
 <0,\,\,(1))
+\frac{1}{f(x)}=g(x),\,\,(2))
α) Να δείξετε ότι για κάθε

ειναι
 \leq -2)
β) Αν
=-2)
και η
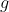
είναι συνεχής στο
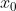
τότε και η
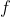
είναι συνεχής στο
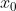
Υπάρχει και γ) ερώτημα αλλά ας το δούμε μετά.
α) Θεωρούμε την συνάρτηση h(x)=x+(1/x)=((x^2)+1)/x με πεδίο ορισμού το Α=[-1,0). Η h είναι συνεχής και παραγωγίσιμη στο Α με πρώτη παράγωγο h΄(x)=1-(1/(x^2))=((x^2)-1)/(x^2)
h΄(x)=0 => x^2=1 => x=-1 (εφόσον -1<=x<0)
Η h είναι συνεχής στο [-1,0), παραγωγίσιμη στο (-1,0) και ισχύει h΄(x)<0 για κάθε x ανήκει (-1,0). Επομένως η h είναι γνησίως φθίνουσα στο [1,0). Επειδή η h είναι γνησίως φθίνουσα στο Α τότε είναι 1-1 και συνεπώς αντιστρέψιμη.
Επειδή lim(x->0-)(1/x)=-oo και lim(x->0-)x=0 τότε lim(x->0-)h(x)=-oo
h(-1)=-2
Η h είναι συνεχής και γνησίως φθίνουσα στο [-1,0), οπότε h(A)=h([-1,0))=(-oo,-2]=B
Άρα h(x)<=-2 για κάθε x ανήκει [-1,0)
Η g γράφεται στη μορφή g(x)=(hof)(x)=h(f(x)), x ανήκει R με -1<=f(x)<0 για κάθε x ανήκει R.
Άρα h(f(x))<=-2 => g(x)<=-2 για κάθε x ανήκει R
β) Εφόσον η h είναι αντιστρέψιμη, έχουμε:
g(x)=h(f(x)) <=> f(x)=(h-1)(g(x)), x ανήκει R
Η μοναδική λύση της εξίσωσης h(x)=-2 είναι η x=-1, δηλαδή h(x)=-2 <=> x=-1.
g(x0)=-2 <=> h(f(x0))=h(-1) <=> f(x0)=-1 (η h είναι 1-1)
Είναι f(x0)=(h-1)(g(x0))
Η h είναι συνεχής στο f(x0)=-1. Επομένως η (h-1) είναι συνεχής στο h(f(x0))=h(-1)=-2.
Η g είναι συνεχής στο x0 και η (h-1) είναι συνεχής στο g(x0)=-2=h(f(x0)). Επομένως η f είναι συνεχής στο x0.