eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.957 μηνύματα.

31-07-20

17:52
Ειδα σημερα τυχαια σε μια δημοφιλης σελιδα του youtube που λεγανε κατι τυπαδες ή προσπαθουσαν να καταλαβουν γτ απο ενα σημειο σε ενα αλλο η πιο συντομη οδος ειναι η ευθεια.Σκεφτηκα λοιπον μια προφανης αποδειξη η οποια δεν ξερω κατα ποσον ειναι τοσο σωστη.
Λεω λοιπον εχω 2 παλουκια τοποθετημενα στα σημεια Α και Β αντιστοιχα.Εστω σημειο Κ τυχαιο σημειο εκτος του ευθυγραμμου τμηματος ΑΒ.Απο το σημειο Κ φερνω την καθετο ΚΔ στην ΑΒ.Σχηματιζονται 2 ορθογωνια τριγωνα ΚΑΔ,ΚΔΒ.Η ΚΑ,ΚΒ ειναι υποτεινουσες των 2 ορθογωνιων τριγωνων.Αρα ΚΑ>ΑΔ ΚΒ>ΒΔ Επομενως ΚΑ+ΚΒ>ΑΔ+ΔΒ=ΑΒ.Δηλαδη αν ακολουθησουμε την διαδρομη απο το παλουκι Α στο Κ και μετα στο Β η αποσταση ειναι μεγαλυτερη απο το παλουκι Α στο παλουκι Β.Πως σας ακουγεται σαν αποδειξη?
Λεω λοιπον εχω 2 παλουκια τοποθετημενα στα σημεια Α και Β αντιστοιχα.Εστω σημειο Κ τυχαιο σημειο εκτος του ευθυγραμμου τμηματος ΑΒ.Απο το σημειο Κ φερνω την καθετο ΚΔ στην ΑΒ.Σχηματιζονται 2 ορθογωνια τριγωνα ΚΑΔ,ΚΔΒ.Η ΚΑ,ΚΒ ειναι υποτεινουσες των 2 ορθογωνιων τριγωνων.Αρα ΚΑ>ΑΔ ΚΒ>ΒΔ Επομενως ΚΑ+ΚΒ>ΑΔ+ΔΒ=ΑΒ.Δηλαδη αν ακολουθησουμε την διαδρομη απο το παλουκι Α στο Κ και μετα στο Β η αποσταση ειναι μεγαλυτερη απο το παλουκι Α στο παλουκι Β.Πως σας ακουγεται σαν αποδειξη?

31-07-20

18:40
Αυτό που απέδειξες βασικά είναι ότι σε κάθε τρίγωνο το άθροισμα των δύο πλευρών είναι μεγαλύτερο από την τρίτη πλευρά, κάτι που αποτελεί υποπερίπτωση της γενικότερης αρχής που ήθελες να αποδείξεις. Μία προσέγγιση μου θα πρότεινα είναι να θεωρήσεις το γνωστό σύστημα αξόνων χ'χ και y'y. Έστω ότι η ευθεία ταυτίζεται με τον άξονα χ'χ(οπότε παίρνεις στον χ'χ δύο σημεία Α και Β). Θεωρείς επίσης ένα κινούμενο σημείο Σ. Αν αυτό για να μεταβεί από το Α στο Β δεν ακολουθήσει την ευθεία ( τον χ'χ) προφανώς θα μετατοπιστεί και κατακόρυφα. Δηλαδή για κάποιες τουλάχιστον στοιχειώδεις μετατοπίσεις dx θα κάνει και από μία dy οπότε συνολικά θα κάνει την ds = sqrt( dx^2 + dy^2) (πυθαγόρειο) Ισχύει προφανώς ds> dx άρα και η συνολική απόσταση θα είναι μεγαλύτερη από την αντίστοιχη που θα διένυε πάνω στην ευθεία. Επομένως οποιαδήποτε διαδρομή διαφορετική της ευθείας είναι μεγαλύτερη απο αυτήν.
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.957 μηνύματα.

31-07-20

18:41
μα αυτο απεδειξα φιλε μου και εγω τι υποπεριπτωση λεςΑυτό που απέδειξες βασικά είναι ότι σε κάθε τρίγωνο το άθροισμα των δύο πλευρών είναι μεγαλύτερο από την τρίτη πλευρά, κάτι που αποτελεί υποπερίπτωση της γενικότερης αρχής που ήθελες να αποδείξεις. Μία προσέγγιση μου θα πρότεινα είναι να θεωρήσεις το γνωστό σύστημα αξόνων χ'χ και y'y. Έστω ότι η ευθεία ταυτίζεται με τον άξονα χ'χ(οπότε παίρνεις στον χ'χ δύο σημεία Α και Β). Θεωρείς επίσης ένα κινούμενο σημείο Σ. Αν αυτό για να μεταβεί από το Α στο Β δεν ακολουθήσει την ευθεία ( τον χ'χ) προφανώς θα μετατοπιστεί και κατακόρυφα. Δηλαδή για κάθε στοιχειώδη μετατόπιση dx θα κάνει και μία dy οπότε συνολικά θα κάνει την ds = sqrt( dx^2 + dy^2) (πυθαγόρειο) Ισχύει προφανώς ds> dx άρα και η συνολική απόσταση θα είναι μεγαλύτερη από την αντίστοιχη που θα διένυε πάνω στην ευθεία. Επομένως οποιαδήποτε διαδρομή διαφορετική της ευθείας είναι μεγαλύτερη απο αυτήν.


31-07-20

18:44
Το απέδειξες μόνο για την περίπτωση που η εναλλακτική διαδρομή αποτελείται από δύο ευθύγραμμα τμήματα.( AK, BK)μα αυτο απεδειξα φιλε μου και εγω τι υποπεριπτωση λες
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.957 μηνύματα.

31-07-20

18:46
μα και συ πυθαγορειο χρησιμοποιεις αρα ευθυγραμμα τμηματαΤο απέδειξες μόνο για την περίπτωση που η εναλλακτική διαδρομή αποτελείται από δύο ευθύγραμμα τμήματα.( AK, BK)

31-07-20

18:50
Εγώ ανέλυσα την διαδρομή σε στοιχειώδη ευθύγραμμα τμήματα ds βασικά ώστε να πάρω το πυθαγόρειο για κάθε τμήμα. Η ίδια η διαδρομή δεν χρειάζεται να είναι δύο ευθύγραμμα τμήματα. Μπορεί να είναι και καμπύλη. Η βασική ιδέα ίδια είναι.μα και συ πυθαγορειο χρησιμοποιεις αρα ευθυγραμμα τμηματα
Μάρκος Βασίλης
Πολύ δραστήριο μέλος
Ο Βασίλης αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 29 ετών, Διδακτορικός και μας γράφει από Καισαριανή (Αττική). Έχει γράψει 1.871 μηνύματα.

03-08-20

23:27
Αυτό που απέδειξες βασικά είναι ότι σε κάθε τρίγωνο το άθροισμα των δύο πλευρών είναι μεγαλύτερο από την τρίτη πλευρά, κάτι που αποτελεί υποπερίπτωση της γενικότερης αρχής που ήθελες να αποδείξεις. Μία προσέγγιση μου θα πρότεινα είναι να θεωρήσεις το γνωστό σύστημα αξόνων χ'χ και y'y. Έστω ότι η ευθεία ταυτίζεται με τον άξονα χ'χ(οπότε παίρνεις στον χ'χ δύο σημεία Α και Β). Θεωρείς επίσης ένα κινούμενο σημείο Σ. Αν αυτό για να μεταβεί από το Α στο Β δεν ακολουθήσει την ευθεία ( τον χ'χ) προφανώς θα μετατοπιστεί και κατακόρυφα. Δηλαδή για κάποιες τουλάχιστον στοιχειώδεις μετατοπίσεις dx θα κάνει και από μία dy οπότε συνολικά θα κάνει την ds = sqrt( dx^2 + dy^2) (πυθαγόρειο) Ισχύει προφανώς ds> dx άρα και η συνολική απόσταση θα είναι μεγαλύτερη από την αντίστοιχη που θα διένυε πάνω στην ευθεία. Επομένως οποιαδήποτε διαδρομή διαφορετική της ευθείας είναι μεγαλύτερη απο αυτήν.
Στα προφανή κρύβονται τα μεγαλύτερα λάθη/παραλείψεις στις αποδείξεις. Προφανώς (pun intended) θα μπορούσε να κάνει απλώς «μπρος-πίσω» το σημείο και να μην μετατοπιστεί κατακόρυφα, οπότε το παραπάνω επιχείρημα δε δουλεύει - αλλά, είναι τετριμμένο να αποδείξουμε ότι αυτό δεν είναι μία από τις ελάχιστες διαδρομές.
Εγώ ανέλυσα την διαδρομή σε στοιχειώδη ευθύγραμμα τμήματα ds βασικά ώστε να πάρω το πυθαγόρειο για κάθε τμήμα. Η ίδια η διαδρομή δεν χρειάζεται να είναι δύο ευθύγραμμα τμήματα. Μπορεί να είναι και καμπύλη. Η βασική ιδέα ίδια είναι.
Ας χρησιμοποιούμε καλύτερα όρους συμβατικής ανάλυσης - ε-δ κ.λπ.. Η διαίσθηση είναι σωστή, αλλά δεν είναι τυπική διατύπωση η παραπάνω.
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.957 μηνύματα.

03-08-20

23:29
εντελει αυτη η αποδειξη που εδωσα δεν ειναι σωστη?Στα προφανή κρύβονται τα μεγαλύτερα λάθη/παραλείψεις στις αποδείξεις. Προφανώς (pun intended) θα μπορούσε να κάνει απλώς «μπρος-πίσω» το σημείο και να μην μετατοπιστεί κατακόρυφα, οπότε το παραπάνω επιχείρημα δε δουλεύει - αλλά, είναι τετριμμένο να αποδείξουμε ότι αυτό δεν είναι μία από τις ελάχιστες διαδρομές.
Ας χρησιμοποιούμε καλύτερα όρους συμβατικής ανάλυσης - ε-δ κ.λπ.. Η διαίσθηση είναι σωστή, αλλά δεν είναι τυπική διατύπωση η παραπάνω.

03-08-20

23:50
Εχεις δικιο οτι θα μπορουσε να παει μπρος πισω αλλα το θεωρησα προφανες οτι τοτε θα κανει μεγαλυτερη αποσταση και δεν το ανεφερα. Ηδη το ποστ μου ηταν αρκετα μεγαλο. Το θεμα ηταν τι συμβαινει στην μη προφανη περιπτωση. Η διατυπωση πως θα επρεπε να ηταν?
Μάρκος Βασίλης
Πολύ δραστήριο μέλος
Ο Βασίλης αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 29 ετών, Διδακτορικός και μας γράφει από Καισαριανή (Αττική). Έχει γράψει 1.871 μηνύματα.

04-08-20

00:38
@eukleidhs1821 Την ίδια ιδέα έχετε, απλά εσύ υποθέτεις ότι η διαδρομή είναι, ουσιαστικά, τεθλασμένη γραμμή, ενώ μπορεί να μην είναι.
Αρχικά, να τοποθετήσουμε καλά το πρόβλημα. Αν θεωρήσουμε δύο σημεία A,B σε ένα καρτεσιανό επίπεδο με άξονες που (modulo στροφή και μεταφορά) είναι τέτοιοι ώστε A=(0,0) και B=(b,0) τότε αναζητούμε τη συνεχή και παραγωγίσιμη συνάρτηση f που ελαχιστοποιεί την παράσταση:
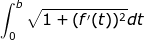
Η λύση είναι τετριμμένη.
Πάντως, το πρόβλημα μπορεί να γραφτεί και λίγο γενικότερα:
Αν θεωρήσουμε δύο σημεία A,B σε ένα καρτεσιανό επίπεδο με άξονες που (modulo στροφή και μεταφορά) είναι τέτοιοι ώστε A=(0,0) και B=(b,0) τότε αναζητούμε τη συνεχή συνάρτηση f που ελαχιστοποιεί την παράσταση:
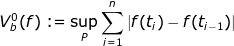
όπου
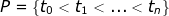 είναι μία διαμέριση του [0,b] - η παραπάνω παράσταση λέγεται κύμανση της f στο [0,b]. Και πάλι, είναι εύκολο να δείξεις ότι η συνάρτηση που θες είναι η σταθερή f=0. Τώρα, μπορείς να το πας ένα κλικ παραπάνω και να αφαιρέσεις την υπόθεση της συνέχειας - στη θέση της πρέπει να υποθέσουμε ότι η συνάρτηση είναι φραγμένης κύμανσης, για να έχει νόημα το πρόβλημα - οπότε θα βρεις ότι όσες συναρτήσεις μας κάνουν τη δουλειά είναι η f=0 και αυτές που είναι σχεδόν παντού ίσες με αυτήν (ως προς το μέτρο Lebesgue).
είναι μία διαμέριση του [0,b] - η παραπάνω παράσταση λέγεται κύμανση της f στο [0,b]. Και πάλι, είναι εύκολο να δείξεις ότι η συνάρτηση που θες είναι η σταθερή f=0. Τώρα, μπορείς να το πας ένα κλικ παραπάνω και να αφαιρέσεις την υπόθεση της συνέχειας - στη θέση της πρέπει να υποθέσουμε ότι η συνάρτηση είναι φραγμένης κύμανσης, για να έχει νόημα το πρόβλημα - οπότε θα βρεις ότι όσες συναρτήσεις μας κάνουν τη δουλειά είναι η f=0 και αυτές που είναι σχεδόν παντού ίσες με αυτήν (ως προς το μέτρο Lebesgue).
Το πρόβλημα της εύρεσης της «ελάχιστης διαδρομής» μεταξύ δύο σημείων σε μία «επιφάνεια» - ριμάννεια πολλαπλότητα - και όχι απλά στο επίπεδο έχει άμεσα να κάνει με αυτό που λέμε γεωδαισιακή.
Εχεις δικιο οτι θα μπορουσε να παει μπρος πισω αλλα το θεωρησα προφανες οτι τοτε θα κανει μεγαλυτερη αποσταση και δεν το ανεφερα. Ηδη το ποστ μου ηταν αρκετα μεγαλο. Το θεμα ηταν τι συμβαινει στην μη προφανη περιπτωση. Η διατυπωση πως θα επρεπε να ηταν?
Αρχικά, να τοποθετήσουμε καλά το πρόβλημα. Αν θεωρήσουμε δύο σημεία A,B σε ένα καρτεσιανό επίπεδο με άξονες που (modulo στροφή και μεταφορά) είναι τέτοιοι ώστε A=(0,0) και B=(b,0) τότε αναζητούμε τη συνεχή και παραγωγίσιμη συνάρτηση f που ελαχιστοποιεί την παράσταση:
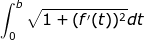
Η λύση είναι τετριμμένη.
Πάντως, το πρόβλημα μπορεί να γραφτεί και λίγο γενικότερα:
Αν θεωρήσουμε δύο σημεία A,B σε ένα καρτεσιανό επίπεδο με άξονες που (modulo στροφή και μεταφορά) είναι τέτοιοι ώστε A=(0,0) και B=(b,0) τότε αναζητούμε τη συνεχή συνάρτηση f που ελαχιστοποιεί την παράσταση:
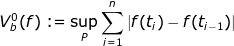
όπου
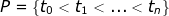
Το πρόβλημα της εύρεσης της «ελάχιστης διαδρομής» μεταξύ δύο σημείων σε μία «επιφάνεια» - ριμάννεια πολλαπλότητα - και όχι απλά στο επίπεδο έχει άμεσα να κάνει με αυτό που λέμε γεωδαισιακή.

04-08-20

01:44
Ο πρώτος τρόπος που προτείνεις με τον τύπο για τον υπολογισμό του μήκους καμπύλης δεν νομίζω να επαρκεί αφού αφορά μόνο σε παραγωγίσιμες συναρτήσεις (αποκλείει πχ την τεθλασμένη γραμμή εκτος κιαν σπάσεις το ολοκλήρωμα σε δύο, αρα και την καμπύλη στα δύο). Επισης χρειάζεται απο μόνος του απόδειξη για την οποία δε γλιτώνεις τη διαδικασία που ακολούθησα έτσι κιαλλιώς ( σπας την καμπύλη σε τμήματα dl και παίρνεις πυθαγόρειο) . Σχετικά με τον δεύτερο πιο γενικό τρόπο, η κύμανση πώς προκύπτει ότι πρέπει να είναι ελάχιστη για να ειναι η διαδρομή ελάχιστη? Τέλος στο ένα κλικ παραπάνω σε έχασα τελείως, προφανώς (αγαπημένη λέξη) επειδή δεν είμαι εξοικειωμένος με τις έννοιες που χρησιμοποιείς( μέτρο lebesgue ,φραγμένη κύμανση, sup υποθέτω συμβολίζει τον διαμερισμό?). Ριμάννια πολλαπλότητα είναι μια μη επίπεδη επιφάνεια? Αυτό που είναι σίγουρο είναι πως το post δεν έπρεπε να ανέβει σε forum γυμνασίου xD@eukleidhs1821 Την ίδια ιδέα έχετε, απλά εσύ υποθέτεις ότι η διαδρομή είναι, ουσιαστικά, τεθλασμένη γραμμή, ενώ μπορεί να μην είναι.
Αρχικά, να τοποθετήσουμε καλά το πρόβλημα. Αν θεωρήσουμε δύο σημεία A,B σε ένα καρτεσιανό επίπεδο με άξονες που (modulo στροφή και μεταφορά) είναι τέτοιοι ώστε A=(0,0) και B=(b,0) τότε αναζητούμε τη συνεχή και παραγωγίσιμη συνάρτηση f που ελαχιστοποιεί την παράσταση:
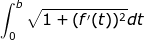
Η λύση είναι τετριμμένη.
Πάντως, το πρόβλημα μπορεί να γραφτεί και λίγο γενικότερα:
Αν θεωρήσουμε δύο σημεία A,B σε ένα καρτεσιανό επίπεδο με άξονες που (modulo στροφή και μεταφορά) είναι τέτοιοι ώστε A=(0,0) και B=(b,0) τότε αναζητούμε τη συνεχή συνάρτηση f που ελαχιστοποιεί την παράσταση:
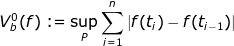
όπουείναι μία διαμέριση του [0,b] - η παραπάνω παράσταση λέγεται κύμανση της f στο [0,b]. Και πάλι, είναι εύκολο να δείξεις ότι η συνάρτηση που θες είναι η σταθερή f=0. Τώρα, μπορείς να το πας ένα κλικ παραπάνω και να αφαιρέσεις την υπόθεση της συνέχειας - στη θέση της πρέπει να υποθέσουμε ότι η συνάρτηση είναι φραγμένης κύμανσης, για να έχει νόημα το πρόβλημα - οπότε θα βρεις ότι όσες συναρτήσεις μας κάνουν τη δουλειά είναι η f=0 και αυτές που είναι σχεδόν παντού ίσες με αυτήν (ως προς το μέτρο Lebesgue).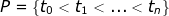
Το πρόβλημα της εύρεσης της «ελάχιστης διαδρομής» μεταξύ δύο σημείων σε μία «επιφάνεια» - ριμάννεια πολλαπλότητα - και όχι απλά στο επίπεδο έχει άμεσα να κάνει με αυτό που λέμε γεωδαισιακή.
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.957 μηνύματα.

04-08-20

04:59
sup ειναι το ελαχιστο ανω φραγμα φιλεΟ πρώτος τρόπος που προτείνεις με τον τύπο για τον υπολογισμό του μήκους καμπύλης δεν νομίζω να επαρκεί αφού αφορά μόνο σε παραγωγίσιμες συναρτήσεις (αποκλείει πχ την τεθλασμένη γραμμή εκτος κιαν σπάσεις το ολοκλήρωμα σε δύο, αρα και την καμπύλη στα δύο). Επισης χρειάζεται απο μόνος του απόδειξη για την οποία δε γλιτώνεις τη διαδικασία που ακολούθησα έτσι κιαλλιώς ( σπας την καμπύλη σε τμήματα dl και παίρνεις πυθαγόρειο) . Σχετικά με τον δεύτερο πιο γενικό τρόπο, η κύμανση πώς προκύπτει ότι πρέπει να είναι ελάχιστη για να ειναι η διαδρομή ελάχιστη? Τέλος στο ένα κλικ παραπάνω σε έχασα τελείως, προφανώς (αγαπημένη λέξη) επειδή δεν είμαι εξοικειωμένος με τις έννοιες που χρησιμοποιείς( μέτρο lebesgue ,φραγμένη κύμανση, sup υποθέτω συμβολίζει τον διαμερισμό?). Ριμάννια πολλαπλότητα είναι μια μη επίπεδη επιφάνεια? Αυτό που είναι σίγουρο είναι πως το post δεν έπρεπε να ανέβει σε forum γυμνασίου xD
Μάρκος Βασίλης
Πολύ δραστήριο μέλος
Ο Βασίλης αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 29 ετών, Διδακτορικός και μας γράφει από Καισαριανή (Αττική). Έχει γράψει 1.871 μηνύματα.

04-08-20

13:38
Ο πρώτος τρόπος που προτείνεις με τον τύπο για τον υπολογισμό του μήκους καμπύλης δεν νομίζω να επαρκεί αφού αφορά μόνο σε παραγωγίσιμες συναρτήσεις (αποκλείει πχ την τεθλασμένη γραμμή εκτος κιαν σπάσεις το ολοκλήρωμα σε δύο, αρα και την καμπύλη στα δύο). Επισης χρειάζεται απο μόνος του απόδειξη για την οποία δε γλιτώνεις τη διαδικασία που ακολούθησα έτσι κιαλλιώς ( σπας την καμπύλη σε τμήματα dl και παίρνεις πυθαγόρειο) . Σχετικά με τον δεύτερο πιο γενικό τρόπο, η κύμανση πώς προκύπτει ότι πρέπει να είναι ελάχιστη για να ειναι η διαδρομή ελάχιστη? Τέλος στο ένα κλικ παραπάνω σε έχασα τελείως, προφανώς (αγαπημένη λέξη) επειδή δεν είμαι εξοικειωμένος με τις έννοιες που χρησιμοποιείς( μέτρο lebesgue ,φραγμένη κύμανση, sup υποθέτω συμβολίζει τον διαμερισμό?). Ριμάννια πολλαπλότητα είναι μια μη επίπεδη επιφάνεια? Αυτό που είναι σίγουρο είναι πως το post δεν έπρεπε να ανέβει σε forum γυμνασίου xD
Ο τύπος αποτελεί τον ορισμό του μήκους τμήματος παραγωγίσιμης συνάρτησης (με ολοκληρώσιμη παράγωγο) και αυτό που αναφέρεις είναι η διαίσθηση πίσω από τον τύπο. Ωστόσο, δε χρειάζεται απόδειξη και η δικαιολόγηση δε γίνεται με «στοιχειώδη» μήκη, πλέον, αλλά με τον ορισμό του ολοκληρώματος (Riemann, στην προκειμένη). Τώρα, το ότι η f είναι παραγωγίσιμη δεν είναι θέμα, αφού μπορούμε να υποθέσουμε για παράδειγμα ότι είναι κατά τμήματα παραγωγίσιμη (με ολοκληρώσιμη παράγωγο) οπότε να πιάσουμε και τις τεθλασμένες γραμμές.
Για τη «γενίκευση», αν πάρεις τον ορισμό του ολοκληρώματος για το μήκος μίας καμπύλης - χωρίς να υποθέσεις κάτι για την παραγωγισιμότητα της f - τότε θα δεις ότι αυτό που εμφανίζεται είναι ουσιαστική η κύμανση της f, οπότε είναι φυσιολογικό να θεωρήσουμε ότι αυτή εκφράζει κάτι σχετικό με το μήκος της γραφικής της παράστασης, όταν αυτό έχει νόημα.
Τώρα, οι πολλαπλότητες, γενικά, είναι (τοπλογικοί) χώροι που τοπικά «μοιάζουν» ευκλείδειοι - σε ό,τι έχει να κάνει με την τοπολογία τους (και σε έναν βαθμό, με τη γεωμετρία τους). Δεν είναι απλά μία επίπεδη επιφάνεια, αλλά κάτι αρκετά γενικότερο - όπως και η γεωδαισιακή, που είναι, επί της ουσίας, η τροχιά ενός κινητού που κινείται με σταθερή (διανυσματική) ταχύτητα πάνω σε μία «επιφάνεια».
Thanos_D
Νεοφερμένο μέλος
Ο Thanos_D αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 24 ετών και Φοιτητής του τμήματος Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών (Θεσσαλονίκη). Έχει γράψει 76 μηνύματα.

04-08-20

16:15
Από περιέργεια, αυτά τι επιπέδου μαθηματικά είναι; Είμαι απόφοιτος που έδωσε 2η φορά, και προφανώς δεν καταλαβαίνω παρά μερικές έννοιες. Είναι μαθηματικά που θα τα συναντήσω πχ στους ΗΜΜΥ που θα είμαι;Ο τύπος αποτελεί τον ορισμό του μήκους τμήματος παραγωγίσιμης συνάρτησης (με ολοκληρώσιμη παράγωγο) και αυτό που αναφέρεις είναι η διαίσθηση πίσω από τον τύπο. Ωστόσο, δε χρειάζεται απόδειξη και η δικαιολόγηση δε γίνεται με «στοιχειώδη» μήκη, πλέον, αλλά με τον ορισμό του ολοκληρώματος (Riemann, στην προκειμένη). Τώρα, το ότι η f είναι παραγωγίσιμη δεν είναι θέμα, αφού μπορούμε να υποθέσουμε για παράδειγμα ότι είναι κατά τμήματα παραγωγίσιμη (με ολοκληρώσιμη παράγωγο) οπότε να πιάσουμε και τις τεθλασμένες γραμμές.
Για τη «γενίκευση», αν πάρεις τον ορισμό του ολοκληρώματος για το μήκος μίας καμπύλης - χωρίς να υποθέσεις κάτι για την παραγωγισιμότητα της f - τότε θα δεις ότι αυτό που εμφανίζεται είναι ουσιαστική η κύμανση της f, οπότε είναι φυσιολογικό να θεωρήσουμε ότι αυτή εκφράζει κάτι σχετικό με το μήκος της γραφικής της παράστασης, όταν αυτό έχει νόημα.
Τώρα, οι πολλαπλότητες, γενικά, είναι (τοπλογικοί) χώροι που τοπικά «μοιάζουν» ευκλείδειοι - σε ό,τι έχει να κάνει με την τοπολογία τους (και σε έναν βαθμό, με τη γεωμετρία τους). Δεν είναι απλά μία επίπεδη επιφάνεια, αλλά κάτι αρκετά γενικότερο - όπως και η γεωδαισιακή, που είναι, επί της ουσίας, η τροχιά ενός κινητού που κινείται με σταθερή (διανυσματική) ταχύτητα πάνω σε μία «επιφάνεια».
Μάρκος Βασίλης
Πολύ δραστήριο μέλος
Ο Βασίλης αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 29 ετών, Διδακτορικός και μας γράφει από Καισαριανή (Αττική). Έχει γράψει 1.871 μηνύματα.

04-08-20

22:32
Από περιέργεια, αυτά τι επιπέδου μαθηματικά είναι; Είμαι απόφοιτος που έδωσε 2η φορά, και προφανώς δεν καταλαβαίνω παρά μερικές έννοιες. Είναι μαθηματικά που θα τα συναντήσω πχ στους ΗΜΜΥ που θα είμαι;
Σε ένα τμήμα μαθηματικών είναι προπτυχιακού επιπέδου - είχαμε και μάθημα για πολλαπλότητες και μάθημα αλγεβρικής τοπολογίας κ.λπ. - όπως και αρκετά από αυτά θα δεις σε ένα τμήμα φυσικής. Τώρα, σε ό,τι αφορά τα πρώτα, με τα suprema και τα ολοκληρώματα κ.λπ., και ναι και ίσως όχι. Ναι, θα τα δεις ονομαστικά και θα τα χειριστείς λίγο ως έννοιες, αλλά, ανάλογα με το πώς διδάσκεται το μάθημα της ανάλυσης, μπορεί να μην εμβαθύνετε και καθόλου. Για τις συναρτήσεις φραγμένης κύμανσης τώρα, είναι κομβικής σημασίας στον ορισμό του ολοκληρώματος Riemann-Stieltjes το οποίο γενικεύει, κατά μία έννοια, το σύνηθες ολοκλήρωμα Riemann (του λυκείου). Εφαρμογές που ξέρω ότι έχει είναι στη θεωρία πιθανοτήτων και τα οικονομικά, οπότε δεν ξέρω κατά πόσο ασχολείστε με αυτά - ωστόσο, οι συναρτήσεις φραγμένης κύμανσης καθεαυτές είναι μία σημαντική κλάση συναρτήσεων που δεν τη συναντάς μόνο στα ολοκληρώματα Riemann-Stieltjes.
Thanos_D
Νεοφερμένο μέλος
Ο Thanos_D αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 24 ετών και Φοιτητής του τμήματος Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών (Θεσσαλονίκη). Έχει γράψει 76 μηνύματα.

04-08-20

22:43
Μάλιστα, σε ευχαριστώ!Σε ένα τμήμα μαθηματικών είναι προπτυχιακού επιπέδου - είχαμε και μάθημα για πολλαπλότητες και μάθημα αλγεβρικής τοπολογίας κ.λπ. - όπως και αρκετά από αυτά θα δεις σε ένα τμήμα φυσικής. Τώρα, σε ό,τι αφορά τα πρώτα, με τα suprema και τα ολοκληρώματα κ.λπ., και ναι και ίσως όχι. Ναι, θα τα δεις ονομαστικά και θα τα χειριστείς λίγο ως έννοιες, αλλά, ανάλογα με το πώς διδάσκεται το μάθημα της ανάλυσης, μπορεί να μην εμβαθύνετε και καθόλου. Για τις συναρτήσεις φραγμένης κύμανσης τώρα, είναι κομβικής σημασίας στον ορισμό του ολοκληρώματος Riemann-Stieltjes το οποίο γενικεύει, κατά μία έννοια, το σύνηθες ολοκλήρωμα Riemann (του λυκείου). Εφαρμογές που ξέρω ότι έχει είναι στη θεωρία πιθανοτήτων και τα οικονομικά, οπότε δεν ξέρω κατά πόσο ασχολείστε με αυτά - ωστόσο, οι συναρτήσεις φραγμένης κύμανσης καθεαυτές είναι μία σημαντική κλάση συναρτήσεων που δεν τη συναντάς μόνο στα ολοκληρώματα Riemann-Stieltjes.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 1 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 73 μέλη διάβασαν αυτό το θέμα:
- Anna1974
- Thanos_D
- Μήτσος10
- Startx0
- Αναστασία197
- ggl
- το κοριτσι του μαη
- SlimShady
- luisnazariodelima
- Dr House
- jul25
- Μάρκος Βασίλης
- eukleidhs1821
- tsiobieman
- Athens2002
- Στεφανος56
- lnesb
- fmarulezkd
- T C
- roud
- Viedo
- Ggpg
- Rene2004
- nicole1982
- cel123
- Scott
- Nefiki
- Ν.Χ.
- Memetchi
- TonyMontanaEse
- St11
- stefan
- iminspain
- fearless
- Revekka
- Stroka
- Serotonin
- Mukumbura
- Monster Hunter
- Έμμα
- Steffie88
- igeorgeoikonomo
- Scandal
- Κλημεντίνη
- Kostakis45
- hirasawayui
- Johanna Mark
- Unseen skygge
- charmander
- kiyoshi
- J.Cameron
- louminis
- MarcoReus
- MarilynSt
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki

