Γεια σας παιδια...μπορει κανεις να με βοηθησει στα θεματα 11(σελ.354) και 4(σελ 352) του μπαρλα τευχος Α?(δεν μπορω να γραψω ριζες και τετραγωνα στον υπολογιστη) οποιος εχει το βιβλιο και γνωριζει ας με βοηθησει...Ευχαριστω!
Θεμα 4 απο Μπαρλα στη σελιδα 352 (αν εχουμε το ιδιο)
α) Σου ζητα να βρεις το γεωμετρικοο τοπο (τον ονομαζει Cα ) των σημειων Μ του επιπεδου που ειναι εικονες των ζ=χ+yι με χ,y ε IR, που εικανοποιουν τη σχεση
+z-\bar{z}=0)
με
α ε IR
Το μονο που μπορεις να εκμεταλευτεις ειναι την σχεση που σου δινει και σου λεει οτι ισχυει για τους z .Γνωριζω απο θεωρια οτι
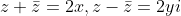
αρα η ισοτητα γινεται:
+2y\iota)
=0 =>2x-α+2y=0 με
α ε IR
Ογεωμετρικος τοπος στον οποιο κινουνται οι οικονες του z ειναι μια ωραιοτατη ευθεια με εξισωση 2x-α+2y=0 με
α ε IR
β) Διαβαζοντας το ερωτημα παιρνουμε τα δεδομενα και το ζητουμενο του. Αρχικα λεει "Αν Α(-1/2, 3/2) ε Cα" αρα καταλαβαινουμε οτι οι συντεταγμενες του Α ικανοποιουν την εξισωση της ευθειας (Cα) .
Για χ=-1/2 και y=3/2 εχω 2*(-1/2)-α+2*3/2=0=>...=>
α=2
Οποτε η εξισωση του Cα ειναι 2χ-2+2y=0 =>
y=-x+1 δηλαδη Ca : y=-x+1, με χ ε ΙR (δεν δινει καποιο περιορισμο για το x)
Μετα λεει "Να προσδιορισετε σημειο Β ε Cα" αυτο ειναι το ζητουμενο, και συμπληρωνει λεγοντας οτι η
μεσοκαθετος του ΑΒ θα περνα απο το
κεντρο του κυκλου με εξισωση |z+1-3i|=β, με β>0
Ξεκιναμε απο την εξισωση του κυκλου και προσδιοριζουμε το κεντρο του |z+1-3i|=β => |z-(-1+3i)|=β , δηλαδη το κεντρο του κυκλου ειναι το Κ(-1,3) (βλ. θεωρια σχολικου βιβλιου για το πως βρηκα το κεντρο του κυκλου)
Αρα το σχημα μεχρι τωρα εχει ως εξης (Πρωτο σχημα)
Η εξισωση της μεσοκαθετου (την ονομαζω
ε ) του ΑΒ ειναι y-yo=λε * (χ-χο) (1) (οπου λε ο συντελεστης διευθυνσης της ευθειας ε)
Το ευθυγραμο τμημα ΑΒ ανηκει στην ευθεια Cα (αφου ως δεδομενα δινει Α ε Cα και Β ε Cα ) αρα εχουν τον ιδιο συντελεστη διευθυνσης με αυτη. Δηλαδη
λΑΒ=
λCα=-1 . ομως οπως γνωριζουμε απο την δευτερα λυκειου, οταν δυο ευθειες ή ευθυγραμμα τμηματα ειναι καθετα μετξυ τους τοτε εχουν αντιθετοαντιστροφους συντελεστες διευθυνσης. Δηλαδη ισχυει
λΑΒ *
λε= -1=> ...=>
λε=1
Επισης η ασκηση λεει οτι το κεντρο Κ του κυκλου διερχεται απο τη μεσοκαθετο του ΑΒ, αρα οι συντεταγμενες του επαληθευουν την εξισωση της μεσοκαθετου του ΑΒ. Μετα απο αυτα η σχεση (1) γινεται y-
yk=1*(x-
xk) =>...=>y=x+4 (η εξισωση της μεσοκαθετου του ΑΒ και στην ουσια η ευθεια ε)
Οπως φαινεται απο το δευτερο σχημα η ευθεια ε περναει απο το μεσο Μ του ΑΒ (λογικο αφου ειναι η μεσοκαθετοςς του). Το σημειο Μ επαληθευει δυο εξισωσεις. Αυτη της ευθειας ε και της ευθειας Cα. Λυνοντα το συστημα των δυο εξισωσεων θα βρουμε τις συντεταγμενες του Μ.
y=x+4
y= -x+1 ...
Αν το λυσεις τοτε βγαινει Μ( -3/2, 5/2)
Ξαναλεω οτι το Μ ειναι το μεσο του Αβ οποτε ισχυει Μ(
(x Α+
xB )/2 , (
yA+
yB)/2 ) .Απο εκει περα εχω
(x Α+
xB )/2 = -3/2 (το εχω βρει απο πανω) =>...=>
xΒ= -5/2 και ομοια βγαινει οτι
yΒ= 7/2
Επομενως οι συντεταγμενες του ζητουμενου Β (βλ. σχημα 3) ειναι Β(-5/2, 7/2) (ο Μπαρλας συμφωνει μαζι μου

)
Οσον αφορα το τελευταιο υποερωτημα. Ζητα την ακτινα του κυκλου (το β ) με κεντρο το Κ ετσι, ωστε ο κυκλος να
εφαπτεται στην ευθεια Cα. Αν δεις απο το σχημα με τον αθλιο κυκλο θα παρατηρησεις οτι στην ουσια ζητα το ευθυγραμο τμημα ΜΚ αφου μονο τοτε (αν δηλαδη β=ΜΚ ) ο κυκλος εφαπτεται στη Cα.
ΜΚ=
}^{2}+{\left(yK-yM \right)}^{2}})
=...=
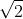
/2
Ελπιζω να βοηθησα και να ειναι το σωστο θεμα !

Αυτα ειναι τα σχηματα
Γεια σας παιδια...μπορει κανεις να με βοηθησει στα θεματα 11(σελ.354) και 4(σελ 352) του μπαρλα τευχος Α?(δεν μπορω να γραψω ριζες και τετραγωνα στον υπολογιστη) οποιος εχει το βιβλιο και γνωριζει ας με βοηθησει...Ευχαριστω!
Θεμα 11 Μπαρλας σελιδα 354
α) Λυνεις την εξισωση κανονικα με διακρινουσα κτλ .Βγαινει Δ= -4(ημθ)^2 <0 για καθε θ ε (0,2π) (Αυτος λεει να λυθει για καθε θ ε [0,2π) αλλα δεν ξερω τι να κανω αν θ=0 αφου βγαινει Δ=0) και Z1= συνθ+iημθ , Z2=συνθ-iημθ
β) Απο εδω και περα δεν ειμαι σιγουρος και θα γραψω πως θα το ελυνα εγω...
Για να βρισκονται οι εικονες των Ζ1,Ζ2 στον μοναδιαιο κυκλο
θα πρεπει οι συντεταγμενες τους να βρισκονται μεταξυ του -1 και του 1 (αν σχηματισεις ενα μοναδιαιο κυκλο τοτε θα δεις γιατι αυτα τα νουμερα)
Εστω Β,Γ οι εικονες των Ζ1,Ζ2 αντιστοιχα, με Β(Χ1,y2) και Γ(Χ2,y2). Για να ανηκουν το Β στο μοναδιαιο κυκλο πρεπει να ισχυει:
-1<=Χ1<=1 και -1<=y1<=1 => (ομως Χ1=συνθ και y1=ημθ)
=> -1<=συνθ<=1 και -1<=ημθ<=1
που ισχυουν για καθε θ ε [0,2π)
Αρα το Β , δηλαδη η εικονα του Ζ1 ανηκει στον μοναδιαιο κυκλο.
Ομοιως αποδεικνυεις οτι το Γ δηλαδη η εικονα του Ζ2 ανηκει στον μοναδιαιο κυκλο.
γ) οι εικονες των Ζ1,Ζ2 κινουνται στον μοναδιαιο κυκλο οπως αποδειξαμε παραπανω
για καθε τιμη του θ ε [0,2π) . Δηλαδη αναλογα με το ποια τιμη εχει το θ ο Ζ1 και ο Ζ2 εινα διαφορετικοι. Το ζητουμενο του ερωτηματος ειναι να βρεις την τιμη του θ για την οποια το |Ζ1-Ζ2| παιρνει τη μεγιστη τιμη.
! θυμιζω οτι το μετρο της διαφορας δυο μιγαδικων ειναι ισο με την αποσταση των εικονων τους (βλ. σελιδα 98 σχολικου βιβλιου)
Ισχυει δηλαδη |Ζ1-Ζ2|= (ΒΓ)
Αρα επι της ουσιας ζητα να βρουμε για ποια τιμη του θ το ΒΓ ειναι μεγιστο.
!θυμιζω οτι σε ενα κυκλο η
μεγιστη αποσταση που μπορουν να εχουν δυο σημεια ειναι 2ρ=δ (οπου
ρ η ακτινα και
δ η διαμετρο του κυκλου)
Και αφου ο κυκλος ειναι μοναδιαιος τοτε ρ=1 ,αρα δ=(ΒΓ)max=2
Επομενως πρεπει να λυσω την εξισωση |Ζ1-Ζ2|= (ΒΓ)max =>|Ζ1-Ζ2|=2 => |συνθ+iημθ-συνθ+iημθ|=2 => |iημθ|=1 =>|ημθ|=1 που ισχυει θ=π/2 ή θ=3π/2 (σε rad)
