mikroaggelaki
Νεοφερμένο μέλος
Ο mikroaggelaki αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 35 ετών. Έχει γράψει 14 μηνύματα.

16-05-21

23:52
1. Διατυπώστε παράδειγμα συνεχούς κατανομής με ασυνεχή αθροιστική για το οποίο το πλήθος των ασυνεχειών να είναι δύο
2. Διατυπώστε παράδειγμα συνεχούς κατανομής με ασυνεχή αθροιστική για το οποίο το πλήθος των ασυνεχειών να είναι ένα αλλά η ασυνέχεια να εμφανίζεται στο εσωτερικό του supp
3. Διατυπώστε παράδειγμα κατανομής με supp που αποτελείται από την ένωση διαστήματος και ξένου ως προς αυτό διακριτού υποσυνόλου των πραγματικών με πλήθος στοιχείων ίσο με δύο
4. Διατυπώσετε παράδειγμα κατανομής με supp που αποτελείται από την ένωση διαστήματος και ξένου ως προς αυτό διακριτού υποσυνόλου των πραγματικών με πλήθος στοιχείων ίσο με ένα αλλά η αθροιστική να εμφανίζει ασυνέχεια και στο "συνεχές" μέρος του στηρίγματος (δηλ. στο προαναφερθέν διάστημα).
2. Διατυπώστε παράδειγμα συνεχούς κατανομής με ασυνεχή αθροιστική για το οποίο το πλήθος των ασυνεχειών να είναι ένα αλλά η ασυνέχεια να εμφανίζεται στο εσωτερικό του supp
3. Διατυπώστε παράδειγμα κατανομής με supp που αποτελείται από την ένωση διαστήματος και ξένου ως προς αυτό διακριτού υποσυνόλου των πραγματικών με πλήθος στοιχείων ίσο με δύο
4. Διατυπώσετε παράδειγμα κατανομής με supp που αποτελείται από την ένωση διαστήματος και ξένου ως προς αυτό διακριτού υποσυνόλου των πραγματικών με πλήθος στοιχείων ίσο με ένα αλλά η αθροιστική να εμφανίζει ασυνέχεια και στο "συνεχές" μέρος του στηρίγματος (δηλ. στο προαναφερθέν διάστημα).
Guest 454371
Επισκέπτης
αυτή τη στιγμή δεν είναι συνδεδεμέν. Δεν έχει γράψει κανένα μήνυμα.

27-05-21

02:32
ελα @nPb ποτε δεν ειναι αργα
bovid19
Εκκολαπτόμενο μέλος
Ο bovid19 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 27 ετών και Πτυχιούχος του τμήματος Οικονομικής Επιστήμης ΟΠΑ. Έχει γράψει 344 μηνύματα.

28-05-21

18:04
Μια συνάρτηση κατανομής πιθανότητας :=P(X\leq x)) (αυτή που λες αθροιστική - στο εξής σκπ) πρέπει να ικανοποιεί τις ακόλουθες ιδιότητες για να είναι καλά ορισμένη.
(αυτή που λες αθροιστική - στο εξής σκπ) πρέπει να ικανοποιεί τις ακόλουθες ιδιότητες για να είναι καλά ορισμένη.
=0, \lim_{x \to \infty}F(x)=1) και επίσης να είναι αύξουσα (όχι απαραίτητα γνησίως) και δεξιά συνεχής. Αν φτιάξεις μια τέτοια συνάρτηση (δεν έχει καμία σημασία αν είναι πολύκλαδη ή όχι) έχεις φτιάξει και μια κατανομή πιθανότητας. Και στις 4 περιπτώσεις το support θα είναι κάποιο υποσύνολο του
και επίσης να είναι αύξουσα (όχι απαραίτητα γνησίως) και δεξιά συνεχής. Αν φτιάξεις μια τέτοια συνάρτηση (δεν έχει καμία σημασία αν είναι πολύκλαδη ή όχι) έχεις φτιάξει και μια κατανομή πιθανότητας. Και στις 4 περιπτώσεις το support θα είναι κάποιο υποσύνολο του ) οπότε
οπότε =0) για κάθε
για κάθε 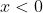 και δεν θα γράφεται. Ζωγράφισε τις συναρτήσεις που θα σου δώσω για να καταλάβεις καλύτερα. Γενικώς μπορείς φτιάξεις άπειρες τέτοιες εφόσον σέβεσαι τις παραπάνω ιδιότητες.
και δεν θα γράφεται. Ζωγράφισε τις συναρτήσεις που θα σου δώσω για να καταλάβεις καλύτερα. Γενικώς μπορείς φτιάξεις άπειρες τέτοιες εφόσον σέβεσαι τις παραπάνω ιδιότητες.
1)Το support εδώ είναι το)
=)
 για
για 
 για
για 
^x) για
για 
ασυνέχεια στα 1, 2.
2)Το support εδώ είναι το)
=)
 για
για 
^x) για
για 
ασυνέχεια στο 2
3)Το support εδώ είναι το
=)
 για
για 
 για
για 
 για
για 
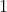 για
για 
4)Το support εδώ είναι το
=)
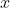 για
για 
 για
για 
 για
για 
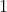 για
για 
ασυνέχεια στο 0.2
Έξτρα άσκηση: Βρες τα) στις 3,4 και το
στις 3,4 και το ) στην 3.
στην 3.
1)Το support εδώ είναι το
ασυνέχεια στα 1, 2.
2)Το support εδώ είναι το
ασυνέχεια στο 2
3)Το support εδώ είναι το
4)Το support εδώ είναι το
ασυνέχεια στο 0.2
Έξτρα άσκηση: Βρες τα
mikroaggelaki
Νεοφερμένο μέλος
Ο mikroaggelaki αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 35 ετών. Έχει γράψει 14 μηνύματα.

29-05-21

10:42
(a) Έστω ℙ = Bin (𝑞, 𝑛) η διωνυμική κατανομή. Έστω και η τυχαία μεταβλητή 𝑋 ∶ ℝ → ℝ, όπου 𝑋(𝑧) = \sqrt {𝑧}. Να βρεθούν: α) το supp, β) η συνάρτηση πιθανότητας, και γ) η αθροιστική συνάρτηση της κατανομής - έστω ℙ_𝑋 που προκύπτει απο τη μεταφορά της 𝑃 μέσω της 𝑋.
(b) Να δειχθεί ότι η αθροιστική συνάρτηση της 𝑁 (𝜇, 𝑣) (𝜇 ∈ ℝ, 𝑣 > 0) είναι συνεχής.
(b) Να δειχθεί ότι η αθροιστική συνάρτηση της 𝑁 (𝜇, 𝑣) (𝜇 ∈ ℝ, 𝑣 > 0) είναι συνεχής.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 1 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 35 μέλη διάβασαν αυτό το θέμα:
-
Φορτώνει...
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki

