Άσκηση στα Μαθηματικά

[Guest 488121]

Να βρεθεί το όριο

 

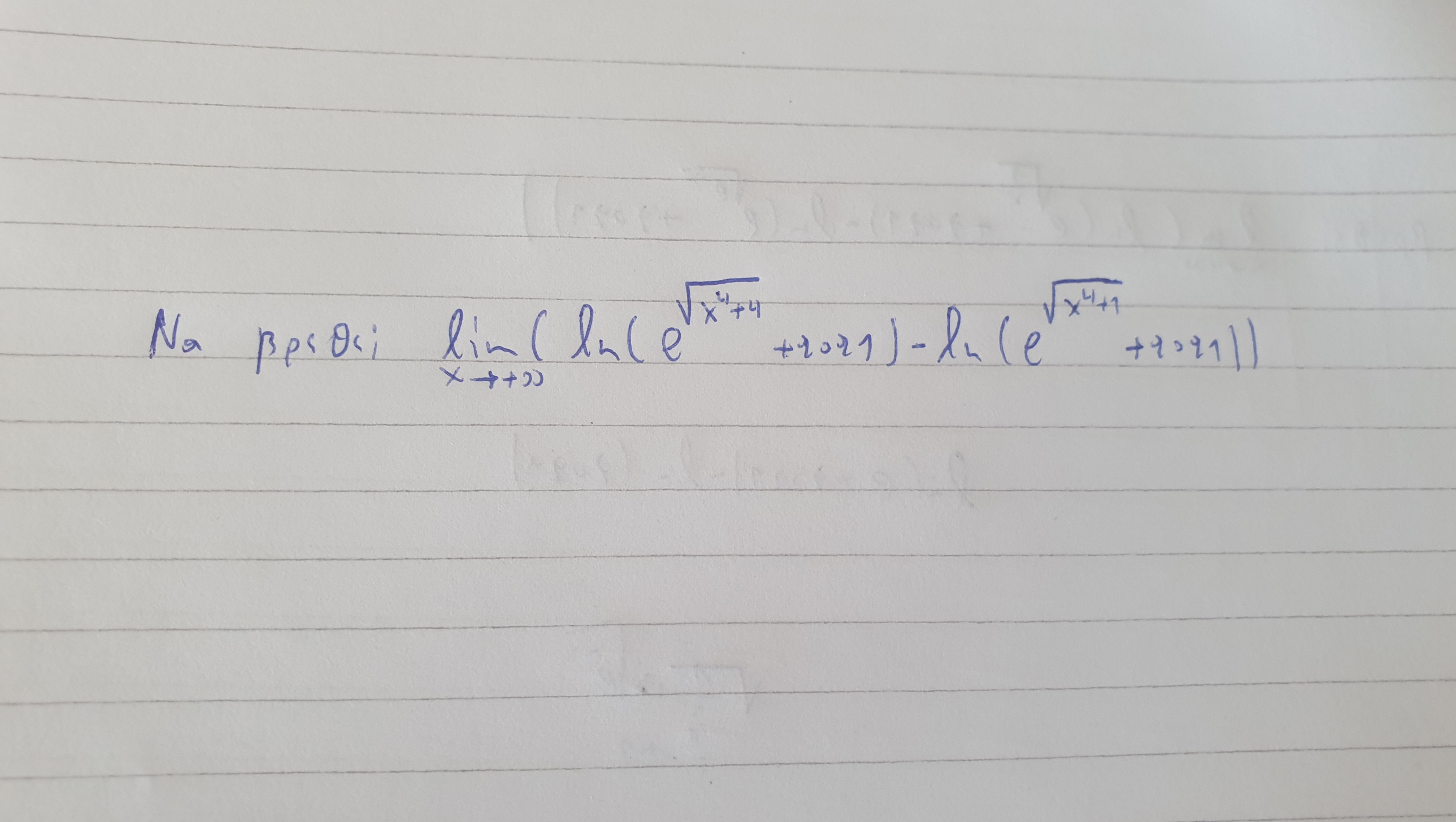
[Samael]

Να βρεθεί το όριο View attachment 83697

Αυτό αξίζει κανείς να το δοκιμάσει με De L'Hospital, χωρίς να ξέρω τι τύχη θα έχει, αλλά γενικά, εφαρμόζοντας ιδιότητες λογαρίθμων, μπορούμε να μείνουμε με τον λογάριθμο του λόγου των δύο ποσοτήτων. Και επειδή για μεγάλα χ οι σταθερές στα υπόριζα γίνονται αμελητέες, οι δύο ποσότητες στον αριθμητή και τον παρονομαστή αντίστοιχα ταυτίζονται. Ως αποτέλεσμα να καταλήγουμε με ln1, που κάνει φυσικά 0 .

 

[Guest 488121]

Αυτό αξίζει κανείς να το δοκιμάσει με De L'Hospital, χωρίς να ξέρω τι τύχη θα έχει, αλλά γενικά, εφαρμόζοντας ιδιότητες λογαρίθμων, μπορούμε να μείνουμε με τον λογάριθμο του λόγου των δύο ποσοτήτων. Και επειδή για μεγάλα χ οι σταθερές στα υπόριζα γίνονται αμελητέες, οι δύο ποσότητες στον αριθμητή και τον παρονομαστή αντίστοιχα ταυτίζονται. Ως αποτέλεσμα να καταλήγουμε με ln1, που κάνει φυσικά 0 .

Είναι ιδιοκατασκευή το όριο. Να σου πω την αλήθεια δεν το έχω δοκιμάσει με dlh . Θα το αφήσω για λίγο και θα δώσω μετά την δικιά μου λύση. Σε ευχαριστώ

Αυτόματη ένωση συνεχόμενων μηνυμάτων: 26 Ιουλίου 2021

Αυτό αξίζει κανείς να το δοκιμάσει με De L'Hospital, χωρίς να ξέρω τι τύχη θα έχει, αλλά γενικά, εφαρμόζοντας ιδιότητες λογαρίθμων, μπορούμε να μείνουμε με τον λογάριθμο του λόγου των δύο ποσοτήτων. Και επειδή για μεγάλα χ οι σταθερές στα υπόριζα γίνονται αμελητέες, οι δύο ποσότητες στον αριθμητή και τον παρονομαστή αντίστοιχα ταυτίζονται. Ως αποτέλεσμα να καταλήγουμε με ln1, που κάνει φυσικά 0 .

Δεν ξέρω κατά πόσο με dlh θα βγαίνει

 

[Samael]

Είναι ιδιοκατασκευή το όριο. Να σου πω την αλήθεια δεν το έχω δοκιμάσει με dlh . Θα το αφήσω για λίγο και θα δώσω μετά την δικιά μου λύση. Σε ευχαριστώ

Αυτόματη ένωση συνεχόμενων μηνυμάτων: 26 Ιουλίου 2021

Δεν ξέρω κατά πόσο με dlh θα βγαίνει

Ναι ο dlh είναι πολύ τζόγος σε τέτοια οριάκια η αλήθεια είναι.
Εγώ θα στοιχημάτιζα οτι δεν βγαίνει με Dlh. Θα πρέπει να καταλήγει σε λούπες. Αλλά ακόμα και εάν βγαίνει, έχει αρκετή δουλειά η παραγώγιση . Αλλά ναι, όποτε μπορέσεις δείξε μας τι έχεις κάνει .

 

[eukleidhs1821]

ξαναγραφτο πιο καθαρα εγω δεν διακρινω καν μετα το εκθετικο τι γραφεις.παντως μοιαζει να κανεις ενα ln και μετα βγαινει αρκετα ευκολα αλλα ξαναγραφτο γτ δεν φαινεται

 

[Unboxholics]

Να βρεθεί το όριο View attachment 83697

Ωραια εγω στο συγκεκριμενο απλως θα εκανα τους λογαριθμους σε ενα κλασμα απο τις ιδιοτητες και αφου ειναι το ιδιο οπως βλεπω σε παρονομαστή κ αριθμητη τοτε εχουμε ln1 το οποίο ισούται με 0.

 

[Guest 488121]

ξαναγραφτο πιο καθαρα εγω δεν διακρινω καν μετα το εκθετικο τι γραφεις.παντως μοιαζει να κανεις ενα ln και μετα βγαινει αρκετα ευκολα αλλα ξαναγραφτο γτ δεν φαινεται

Αυτόματη ένωση συνεχόμενων μηνυμάτων: 26 Ιουλίου 2021

Ωραια εγω στο συγκεκριμενο απλως θα εκανα τους λογαριθμους σε ενα κλασμα απο τις ιδιοτητες και αφου ειναι το ιδιο οπως βλεπω σε παρονομαστή κ αριθμητη τοτε εχουμε ln1 το οποίο ισούται με 0.

Επειδή δεν φαίνεται καλά το ανέβασα ξανά

Αυτόματη ένωση συνεχόμενων μηνυμάτων: 26 Ιουλίου 2021

Επειδή δεν φαίνεται καλά το ανέβασα ξανά

.

 

[stav.mdp]

.

Γειααα
Θα ήθελες τη λύση ή τελικά σου βγήκε το όριο?

 

[Guest 488121]

Γειααα
Θα ήθελες τη λύση ή τελικά σου βγήκε το όριο?

Λύση έχω γιατί είναι ιδιοκατασκευή. Το ανέβασα για να ασχοληθούν και οι υπόλοιποι γιατί είναι δύσκολο όριο. Θα την ανεβάσω την λύση μου αργότερα

Αυτόματη ένωση συνεχόμενων μηνυμάτων: 27 Ιουλίου 2021

Γειααα
Θα ήθελες τη λύση ή τελικά σου βγήκε το όριο?

Το έλυσες?

 

[stav.mdp]

Λύση έχω γιατί είναι ιδιοκατασκευή. Το ανέβασα για να ασχοληθούν και οι υπόλοιποι γιατί είναι δύσκολο όριο. Θα την ανεβάσω την λύση μου αργότερα

Αυτόματη ένωση συνεχόμενων μηνυμάτων: 27 Ιουλίου 2021

Το έλυσες?

Έτσι νομίζω(?)
Θα δω τη λύση σου και ίσως επιβεβαιωθώ.

 

[Alexandros28]

Κάνουμε την ιδιότητα των λογάριθμων που προείπε ο σαμαελ και στο πηλίκο διαιρούμε αριθμητή και πολλαπλασιαστή με οποιοδήποτε από τα 2 εκθετικά. Μετά δείχνουμε ότι το οριο της διαφοράς των ριζικών όταν το x τείνει στο +οο ισούται με 0. Ετσι το τελικό όριο ισούται με ln1=0

Αυτόματη ένωση συνεχόμενων μηνυμάτων: 27 Ιουλίου 2021

Για να δειχτει ότι το όριο της διαφοράς των ριζικών είναι 0 χρειάζεται το γνωστό τυφλοσουρτι της μεθοδολογίας όπου βγάζουμε κοινο παράγοντα και μετά πολλαπλασιάζουμε με τη συζυγη παράσταση κλπ κλπ

 

[Guest 488121]

Εγώ το έβγαλα με θμτ. Εκεί στηρίχτηκε και η δημιουργία του ορίου. Θεωρώ fx την ln(e^x+2021) και κάνεις θμτ σε κατάλληλο διάστημα

 

[Alexandros28]

Καλή η σκέψη αλλά στα χαλάει όλα η ιδιότητα των λογάριθμων και επιτρέπει να αποφύγεις την απροσδιοριστία (+oo) - (+oo) με συντομότερο μονοπάτι. Αυτός ο τρόπος λύσης θα ταιριαζε φανταστικά αν στο δοθεν όριο η αντίστοιχη f ήταν η f(x)=ημ(συνx), όπου δεν έχεις κάτι άλλο να κανεις.

 

[Guest 488121]

Όχι ίσα ίσα σε βοηθάει έτσι όπως το έδωσα διότι βγαίνει f(ρίζα(x^4+4))-f(ρίζα(x^4+1)) κατευθείαν