Άσκηση πιθανοτήτων και απορίες Στατιστικής

[aekarare]

Καλησπερα..μπορει να με βοηθησει καποιος στην παρακατω ασκηση?κυριως στο β ερωτημα..το α ξερω οτι λυνεται με απλη εφαρμογη του τυπου του poisson.

μπορει να βοηθησει καποιος??

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Μάρκος Βασίλης]

Έχεις πολλούς τρόπους να το λύσεις. Ο πιο απλός είναι, ίσως, να δεις ποια είναι η πιθανότητα να έχεις μία ακριβώς κλήση και η πιθανότητα να έχεις καμία κλήση (από το πρώτο ερώτημα). Έπειτα, στο εύρος των τριών ημερών, σκέψου με πόσους συνδυασμούς μπορείς να μοιράσεις αυτήν την κλήση.

Άλλος τρόπος είναι να χρησιμοποιήσεις λίγο τις ιδιότητες της Poisson. Για την ακρίβεια, το άθροισμα ανεξάρτητων τ.μ. Poisson ακολουθεί επίσης κατανομή Poisson με παράμετρο λ το άθροισμα των παραμέτρων.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Unseen skygge]

Από την μια θεωρώ μη εποικοδομητική την απάντηση μου αλλά από την άλλη η συγκεκριμένη άσκηση είναι ότι πιο βασικό από άσκηση μπορεί να πέσει στην κατανομή Poisson και τα 2 της ερωτήματα οπότε για αρχή θα σε συμβούλευα να κάνεις ένα recap την θεωρία

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[aekarare]

Έχεις πολλούς τρόπους να το λύσεις. Ο πιο απλός είναι, ίσως, να δεις ποια είναι η πιθανότητα να έχεις μία ακριβώς κλήση και η πιθανότητα να έχεις καμία κλήση (από το πρώτο ερώτημα). Έπειτα, στο εύρος των τριών ημερών, σκέψου με πόσους συνδυασμούς μπορείς να μοιράσεις αυτήν την κλήση.

Άλλος τρόπος είναι να χρησιμοποιήσεις λίγο τις ιδιότητες της Poisson. Για την ακρίβεια, το άθροισμα ανεξάρτητων τ.μ. Poisson ακολουθεί επίσης κατανομή Poisson με παράμετρο λ το άθροισμα των παραμέτρων.

Απο poisson έχουμε κανει μόνο τον τυπο τον βασικό... Δεν έχουμε δει ιδιότητες.. Τώρα αυτό που λες να βρω την πιθανοτητα να έχω μια κλήση και την πιθανοτητα να έχω 0 κλήσεις μάλλον θέλει διωνυμικη.. Αλλά πως να τα συνδυάσω??

Αυτόματη ένωση συνεχόμενων μηνυμάτων: 9 Ιουλίου 2020

Από την μια θεωρώ μη εποικοδομητική την απάντηση μου αλλά από την άλλη η συγκεκριμένη άσκηση είναι ότι πιο βασικό από άσκηση μπορεί να πέσει στην κατανομή Poisson και τα 2 της ερωτήματα οπότε για αρχή θα σε συμβούλευα να κάνεις ένα recap την θεωρία

Όπως είπα δεν έχουμε κάνει τις ιδιότητες.. Όποτε αφου το β) δεν βγαίνει με τον τυπο του Poisson φανταζομαι θα θέλει άλλη κατανομή

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[aekarare]

γεια σας..εχω μια απορια σχετικα με την στατιστικη..στην παρακατω ασκηση μας δινει α=0,1..γιατι παιρνουμε το 1,886 απο το πινακακι?ναι ξερω γιατι εχουμε 2 βε,ειναι μονοπλευρος και το α=0,1..αυτο που θελω να μου εξηγησει καποιος στην ουσια ειναι πως θα καταλαβαινω τι πρεπει να κανω σε καθε ασκηση?σε μερικες ασκησεις λεμε 1-α=... Δηλαδη στην συγκεκριμενη θα μπορουσαμε να πουμε 1-0,1=0,9 και να παρουμε την διπλα στηλη..μπορει καποιος να με βοηθησει να τα ξεχωρισω??

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[aekarare]

Καλησπέρα.. Εχω μια άσκηση πιθανοτητων η οποία έχει χαρακτηριστεί sos για τις εξετάσεις αλλά δεν μπορώ να λυσω το Β ερωτημα.. Μπορεί κάποιος να βοηθήσει;;

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[aekarare]

Καλησπερα παιδια..μπορει να με βοηθησει καποιος με την επιλυση της παρακατω ασκησης και πιο συγκεκριμενα του ii) ερωτηματος??

μπορει καποιος να βοηθησει??

καποιος??

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[aekarare]

καποιος μια βοηθεια για το 2ο ερωτημα παιδια??

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Samael]

καποιος μια βοηθεια για το 2ο ερωτημα παιδια??

Κάνε "rescale" την poisson .
Εφόσον ξέρεις το λ της poisson για 9-9:10 σε μια μέρα...για τις επόμενες 3 ημέρες,η πιθανότητα να δεχθείς κάποιο τηλεφώνημα στο ίδιο χρονικό διάστημα θα δίνεται απο την Poisson με λ = 3*3 = 9 => λ = 9 .

Εφόσον το διάστημα αυξάνεται,η πιθανότητα να λάβεις κάποιο μήνυμα αυξάνεται ανάλογα .
Άρα X ~ Poisson(9) και ζητάς το P(x=1) .

Ελπίζω να βοήθησα .

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[aekarare]

καλησπερα..θελω να σας ρωτησω σχετικα με μια ασκηση πιθανοτητων..η εκφωνηση λεει:Σε ενα εργοστασιο συμβαινουν 2 ατυχηματα κατα μεσο ορο καθε εβδομαδα.Η πιθανοτητα να συμβουν το πολυ 1 ατυχημα σε 2 εβδομαδες ειναι:....Και σκεφτηκα αφου το λ=2 για μια εβδομαδα,για 2 εβδομαδες που θελει η ασκηση θα εχουμε λ=4..επισης λεει το πολυ ενα αρα παιρνουμε P(x=0)+P(x=1)..κανουμε αντικατασταση στον τυπο του poisson και βγαινει 5e^-4..μπορει να μου πει καποιος αν ειναι σωστη η λυση μου?

 

[Samael]

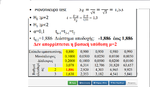
καλησπερα..θελω να σας ρωτησω σχετικα με μια ασκηση πιθανοτητων..η εκφωνηση λεει:Σε ενα εργοστασιο συμβαινουν 2 ατυχηματα κατα μεσο ορο καθε εβδομαδα.Η πιθανοτητα να συμβουν το πολυ 1 ατυχημα σε 2 εβδομαδες ειναι:....Και σκεφτηκα αφου το λ=2 για μια εβδομαδα,για 2 εβδομαδες που θελει η ασκηση θα εχουμε λ=4..επισης λεει το πολυ ενα αρα παιρνουμε P(x=0)+P(x=1)..κανουμε αντικατασταση στον τυπο του poisson και βγαινει 5e^-4..μπορει να μου πει καποιος αν ειναι σωστη η λυση μου?

Μου φαίνεται μια χαρά!
Εναλλακτικά θα μπορούσες να πεις οτι η πιθανότητα να συμβεί το πολύ ένα ατύχημα περιλαμβάνει τις περιπτώσεις :

α)Να μην γίνει ατύχημα ούτε την πρώτη ούτε την δεύτερη εβδομάδα.
β)Να γίνει 1 ατύχημα την πρώτη αλλά κανένα την δεύτερη εβδομάδα
γ)Να μην γίνει ατύχημα την πρώτη αλλά να γίνει 1 την δεύτερη εβδομάδα.

Χ~Poisson(2)

Άρα εαν δεχτούμε οτι ο αριθμός των ατυχημάτων που θα συμβούν την πρώτη εβδομάδα είναι ανεξάρτητος του αριθμού των ατυχημάτων που θα συμβεί την δεύτερη εβδομάδα(και αντίστροφα) :

P(X<=1) = [P(0)]²+2P(0)P(1)

Σε αυτή την περίπτωση κερδίζεις απλά οτι συνεχίζεις να δουλεύεις με το ίδιο λ.

 

[aekarare]

ευχαριστω πολυ..θα ηθελα να ρωτησω και για μια ακομα λυση..λεει η ασκηση(κανονικη κατανομη) οτι το ποσοστο των φοιτητων που δαπανουν στην επαναληψη περισσοτερες απο 30 ωρες ειναι:...(εδινε μ=25,σ=5 και P(0<=Z<=1)=0.3413...εγω εκανα P(X>30)=1-P(X0)=1-P(X<1)=1-0,3413=0,6587..ΕΙΝΑΙ ΣΩΣΤΟ??

Αυτόματη ένωση συνεχόμενων μηνυμάτων: 19 Ιουλίου 2020

P(X>30)=1-P(X0)*

Αυτόματη ένωση συνεχόμενων μηνυμάτων: 19 Ιουλίου 2020

P(x μικροτερο του 30)* γιατι βγαινει καρδουλα..Χαχα

 

[Panagiotis849]

ευχαριστω πολυ..θα ηθελα να ρωτησω και για μια ακομα λυση..λεει η ασκηση(κανονικη κατανομη) οτι το ποσοστο των φοιτητων που δαπανουν στην επαναληψη περισσοτερες απο 30 ωρες ειναι:...(εδινε μ=25,σ=5 και P(0<=Z<=1)=0.3413...εγω εκανα P(X>30)=1-P(X0)=1-P(X<1)=1-0,3413=0,6587..ΕΙΝΑΙ ΣΩΣΤΟ??

Αυτόματη ένωση συνεχόμενων μηνυμάτων: 19 Ιουλίου 2020

P(X>30)=1-P(X0)*

Αυτόματη ένωση συνεχόμενων μηνυμάτων: 19 Ιουλίου 2020

P(x μικροτερο του 30)* γιατι βγαινει καρδουλα..Χαχα

Αν σου έδινε μ, σ και ακολουθεί και κανονική κατανομή, είναι σωστό.

 

[Samael]

ευχαριστω πολυ..θα ηθελα να ρωτησω και για μια ακομα λυση..λεει η ασκηση(κανονικη κατανομη) οτι το ποσοστο των φοιτητων που δαπανουν στην επαναληψη περισσοτερες απο 30 ωρες ειναι:...(εδινε μ=25,σ=5 και P(0<=Z<=1)=0.3413...εγω εκανα P(X>30)=1-P(X0)=1-P(X<1)=1-0,3413=0,6587..ΕΙΝΑΙ ΣΩΣΤΟ??

Αυτόματη ένωση συνεχόμενων μηνυμάτων: 19 Ιουλίου 2020

P(X>30)=1-P(X0)*

Αυτόματη ένωση συνεχόμενων μηνυμάτων: 19 Ιουλίου 2020

P(x μικροτερο του 30)* γιατι βγαινει καρδουλα..Χαχα

Το σωστό είναι 0.1587 .
Έχεις κάνει λάθη :
Η X~N(25,5²)
Η Z~N(0,1)

Οπου z = (x-25)/5

Επίσης σου δίνει το P(0<=z<=1),και όχι το P(z<=1) .
Και ναι η x δεν θα μπορούσε να λάβει αρνητικές τιμές(ώρες διαβάσματος),αλλά η z μπορεί .

 

[aekarare]

Το σωστό είναι 0.1587 .
Έχεις κάνει λάθη :
Η X~N(25,5²)
Η Z~N(0,1)

Οπου z = (x-25)/5

Επίσης σου δίνει το P(0<=z<=1),και όχι το P(z<=1) .
Και ναι η x δεν θα μπορούσε να λάβει αρνητικές τιμές(ώρες διαβάσματος),αλλά η z μπορεί .

Ναι αλλά αφου μου δίνει P(0<=Z<=1) =0.3413.. Πως θα βγάλω το 0.8413 που χρειαζεται για να πω 1-0.8413=0.1587..δεν μου δίνει το 0.8413 αλλά το 0.3413

 

[Samael]

Ναι αλλά αφου μου δίνει P(0<=Z<=1) =0.3413.. Πως θα βγάλω το 0.8413 που χρειαζεται για να πω 1-0.8413=0.1587..δεν μου δίνει το 0.8413 αλλά το 0.3413

Ζητάς :

P(x>30) = 1-P(x<=30) = 1-P(x-25<=5) = 1-P((x-25)/5 <= 1) = 1-P(z<=1)

Όμως P(z<=1) = P(z<=0) + P(0<=z<=1)

Η N(0,1) είναι συμμετρική γύρω απο το 0 οπότε P(z<=0) = 0.5 και το P(0<=z<=1) = 0.3413

Άρα P(x>30) = 1-P(z<=1) = 1- P(z<=0) - P(0<=z<=1) = 1- 0.5 - 0.3413 = 1-0.8413 = 0.1587‬
Τελικά P(x>30) = 0.1587

Ελπίζω αυτό να βοήθησε

 

[aekarare]

Ζητάς :

P(x>30) = 1-P(x<=30) = 1-P(x-25<=5) = 1-P((x-25)/5 <= 1) = 1-P(z<=1)

Όμως P(z<=1) = P(z<=0) + P(0<=z<=1)

Η N(0,1) είναι συμμετρική γύρω απο το 0 οπότε P(z<=0) = 0.5 και το P(0<=z<=1) = 0.3413

Άρα P(x>30) = 1-P(z<=1) = 1- P(z<=0) - P(0<=z<=1) = 1- 0.5 - 0.3413 = 1-0.8413 = 0.1587‬
Τελικά P(x>30) = 0.1587

Ελπίζω αυτό να βοήθησε

Ναι απλα αυτό ήταν πολλαπλης σε εξετάσεις.. Και η κυρία απορία μου ειναι.. Το οτι P(Z<=0) =0.5 δεν θα έπρεπε να το δίνει όπως δίνει το P(0<=Z<=1)??

 

[Samael]

Ναι απλα αυτό ήταν πολλαπλης σε εξετάσεις.. Και η κυρία απορία μου ειναι.. Το οτι P(Z<=0) =0.5 δεν θα έπρεπε να το δίνει όπως δίνει το P(0<=Z<=1)??

Θα μπορούσαν να δίνουν προφανώς κατευθείαν το P(z<=1). Αλλά υποθέτω ήθελαν να παίξουν ύπουλα για να σκεφτείς τις ιδιότητες της τυποποιημένης κανονικής κατανομής.

 

[aekarare]

Θα μπορούσαν να δίνουν προφανώς κατευθείαν το P(z<=1). Αλλά υποθέτω ήθελαν να παίξουν ύπουλα για να σκεφτείς τις ιδιότητες της τυποποιημένης κανονικής κατανομής.

Ζητάς :

P(x>30) = 1-P(x<=30) = 1-P(x-25<=5) = 1-P((x-25)/5 <= 1) = 1-P(z<=1)

Όμως P(z<=1) = P(z<=0) + P(0<=z<=1)

Η N(0,1) είναι συμμετρική γύρω απο το 0 οπότε P(z<=0) = 0.5 και το P(0<=z<=1) = 0.3413

Άρα P(x>30) = 1-P(z<=1) = 1- P(z<=0) - P(0<=z<=1) = 1- 0.5 - 0.3413 = 1-0.8413 = 0.1587‬
Τελικά P(x>30) = 0.1587

Ελπίζω αυτό να βοήθησε

Kαλημερα..ξαναβλεπω το θεμα αυτο,καθως τοτε ειχα καταφερει να κοπω με 4 και τωρα το ξαναδινω..δυστηχως αυτη η απορια με εφαγε..δεν μπορω να καταλαβω με τιποτα πως βγαινει οτι το P(z<=0)=0,5..μπορεις να με βοηθησεις??

 

[Samael]

Kαλημερα..ξαναβλεπω το θεμα αυτο,καθως τοτε ειχα καταφερει να κοπω με 4 και τωρα το ξαναδινω..δυστηχως αυτη η απορια με εφαγε..δεν μπορω να καταλαβω με τιποτα πως βγαινει οτι το P(z<=0)=0,5..μπορεις να με βοηθησεις??

Θα κάνω μια ακόμα απόπειρα.
Λοιπόν όταν αλλάξεις την μεταβλητή σου σε z με τον κατάλληλο μετασχηματισμό της αρχικής μεταβλητής,
δηλαδή z = (x-25)/5,προκύπτει η κανονικοποιημένη κανονική κατανομή.Δηλαδή έχει μέση τιμή το 0 και τυπική απόκλιση το 1.

Αυτή η κατανομή έχει το σχήμα μιας καμπάνας, η οποία είναι συμμετρική ως προς τον άξονα των y.
Δηλαδή εαν την "διπλώσεις" το αριστερό μέρος της(αυτό για z<0) θα συμπέσει πάνω στο δεξί μέρος της(αυτό για z>0). Έτσι εφόσον τα δύο μέρη είναι ισοδύναμα, το εμβαδόν απο κάτω τους είναι ίσο.

Το συνολικό εμβαδόν κάτω απο την καμπάνα πρέπει να δίνει 1,ώστε να αποτελεί κατανομή.
Έτσι εφόσον Ε1+Ε2 = 1 και Ε1=Ε2=Εο συνεπάγεται οτι 2Εο = 1 => Εο = 1/2 =0.5 . Άρα Ε1=Ε2=0.5
Είναι προφανές επομένως οτι το P(z<=0) αναφέρεται στο εμβαδόν κάτω απο το αριστερό τμήμα της καμπύλης της κατανομής και άρα θα είναι ίσο με 0.5 . Έχουμε λοιπόν οτι P(z<=0) = 0.5 .

Ήταν αρκετά αναλυτικό αυτό,σε βοήθησε ;