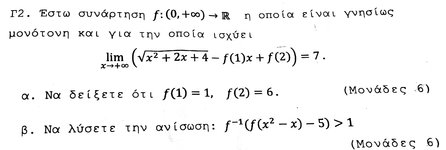Guest 997410
Επισκέπτης
αυτή τη στιγμή δεν είναι συνδεδεμέν. Δεν έχει γράψει κανένα μήνυμα.
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.965 μηνύματα.

02-08-21

14:33
αν το f(1) διαφορο του 1 υπολογιζοντας το οριο βγαζεις οτι θα ειναι +-00 ατοπο.αρα f(1)=1.
μετα βρισκεις το οριο(ριζα(χ^2+2χ+4)-χ)=1. λυνεις ως προς f(2)=κ(χ)-l(x) το οριο του k(x) ειναι 7 και το οριο του l((x) που είναι το ριζα(χ^2+2χ+4)-χ είναι 1.επομένως 7-1=6
στο αλλο ερωτημα εφοσον f γν. αυξουσα εχουμε f(f^-1(f(x^2-x)-5)>f(1) επομένως f(x^2-x)-5>f(1) f(x^2-x)>f(1)+5 f(x^2-x)>5+1=6=f(2) x^2-x>2 x^2-x-2>0 x>2 ή χ<-1
καλο ειναι να μπει και περιορισμος στην συνθεση της f.x^2-x>0 βγαίνει χ>1 ή χ<0 οπότε είναι δεκτή η περιοχή χ>2 και χ<-1
μετα βρισκεις το οριο(ριζα(χ^2+2χ+4)-χ)=1. λυνεις ως προς f(2)=κ(χ)-l(x) το οριο του k(x) ειναι 7 και το οριο του l((x) που είναι το ριζα(χ^2+2χ+4)-χ είναι 1.επομένως 7-1=6
στο αλλο ερωτημα εφοσον f γν. αυξουσα εχουμε f(f^-1(f(x^2-x)-5)>f(1) επομένως f(x^2-x)-5>f(1) f(x^2-x)>f(1)+5 f(x^2-x)>5+1=6=f(2) x^2-x>2 x^2-x-2>0 x>2 ή χ<-1
καλο ειναι να μπει και περιορισμος στην συνθεση της f.x^2-x>0 βγαίνει χ>1 ή χ<0 οπότε είναι δεκτή η περιοχή χ>2 και χ<-1
Alexandros28
Δραστήριο μέλος
Ο Alexandros28 αυτή τη στιγμή δεν είναι συνδεδεμένος. Έχει γράψει 750 μηνύματα.

02-08-21

14:39
Το πρώτο ερώτημα βγαίνει πιο εύκολα μέσω του ορισμού της πλάγιας ασύμπτωτης
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.965 μηνύματα.

02-08-21

14:45
δεν το χουν διδαχτει ακομα ομως οποτε για αυτο ας το λυσει ετσι.αν το χουν διδαχτει ναι συμφερει να το λυσεις με πλαγια ασυμπτωτη πηγαινοντας το 7 μπροστα βλεπεις οτι η f(1)x+7-f(2) ειναι πλαγια ασυμπτωτη στο +00 της συναρτησης με τη ριζα οποτε παιρνεις το οριο limτο ριζικο/χ=f(1) lim(ριζικο-f(1)x)=7-f(2)Το πρώτο ερώτημα βγαίνει πιο εύκολα μέσω του ορισμού της πλάγιας ασύμπτωτης
Guest 997410
Επισκέπτης
αυτή τη στιγμή δεν είναι συνδεδεμέν. Δεν έχει γράψει κανένα μήνυμα.

02-08-21

15:20
Ακαλα ειμαι αχρηστος τελειως ουτε που θα το ελυνα. και νομιζα πως κατι θα γράψω στις πανελελε αλλα ας μην το συζητησουμε. Τεσπα σε ευχαριστωαν το f(1) διαφορο του 1 υπολογιζοντας το οριο βγαζεις οτι θα ειναι +-00 ατοπο.αρα f(1)=1.
μετα βρισκεις το οριο(ριζα(χ^2+2χ+4)-χ)=1. λυνεις ως προς f(2)=κ(χ)-l(x) το οριο του k(x) ειναι 7 και το οριο του l((x) που είναι το ριζα(χ^2+2χ+4)-χ είναι 1.επομένως 7-1=6
στο αλλο ερωτημα εφοσον f γν. αυξουσα εχουμε f(f^-1(f(x^2-x)-5)>f(1) επομένως f(x^2-x)-5>f(1) f(x^2-x)>f(1)+5 f(x^2-x)>5+1=6=f(2) x^2-x>2 x^2-x-2>0 x>2 ή χ<-1
καλο ειναι να μπει και περιορισμος στην συνθεση της f.x^2-x>0 βγαίνει χ>1 ή χ<0 οπότε είναι δεκτή η περιοχή χ>2 και χ<-1
Alexandros28
Δραστήριο μέλος
Ο Alexandros28 αυτή τη στιγμή δεν είναι συνδεδεμένος. Έχει γράψει 750 μηνύματα.

02-08-21

15:30
Φίλε μου δεν χρειάζεσαι τέτοιο χαντάκωμα, αυτοκαταστρέφεσαι. Είσαι ό,τι πείθεις τον εαυτό σου πως είσαι. Με σκληρή δουλειά γίνονται όλα. Πίστεψε με!!!Ακαλα ειμαι αχρηστος τελειως ουτε που θα το ελυνα. και νομιζα πως κατι θα γράψω στις πανελελε αλλα ας μην το συζητησουμε. Τεσπα σε ευχαριστω
Guest 997410
Επισκέπτης
αυτή τη στιγμή δεν είναι συνδεδεμέν. Δεν έχει γράψει κανένα μήνυμα.

02-08-21

15:35
αδερφε, πραγματικα, μετα τα καλοκαιρινα των μαθηματικων στο φροντιστηριο το εχω δει με τελειως αλλο ματι το ζητημα. Για να καταλαβεις ενω αρχικα μπηκα με εναν αερα πάμε να σκισουμε ακουγοντας τον περιγυρο να λεει πως ειναι δυσκολα και οι καλοι μαθητες γραφουν βαση τα ψιλοπαρατησα και να τα αποτελέσματα.Φίλε μου δεν χρειάζεσαι τέτοιο χαντάκωμα, αυτοκαταστρέφεσαι. Είσαι ό,τι πείθεις τον εαυτό σου πως είσαι. Με σκληρή δουλειά γίνονται όλα. Πίστεψε με!!!
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.965 μηνύματα.

02-08-21

15:48
οι καλοι μαθητες γραφουν βαση απο που και ως που??ποιος το λεει αυτο??μην ακους κανεναν.προπονηση θελουν τα μαθηματικα.διαβασε τις μεθολογιες ολες,κατανοησε καλα τη θεωρια και δεν υπαρχει περιπτωση να μην γραψεις καλα.δεν ειναι διαγωνισμος μαθηματικης εταιρειας!!το θεμα που σου λυσα με τα ορια εχετε κανει τις ασυμπτωτες??αν τις εχετε κανει τοτε μην αγχωνεσαι που δεν το λυσες οπως εγω γτ ειναι ολιγον extreme τροπος.με ασυμπτωτες ειναι εφαρμογη της θεωριας.αδερφε, πραγματικα, μετα τα καλοκαιρινα των μαθηματικων στο φροντιστηριο το εχω δει με τελειως αλλο ματι το ζητημα. Για να καταλαβεις ενω αρχικα μπηκα με εναν αερα πάμε να σκισουμε ακουγοντας τον περιγυρο να λεει πως ειναι δυσκολα και οι καλοι μαθητες γραφουν βαση τα ψιλοπαρατησα και να τα αποτελέσματα.
Guest 997410
Επισκέπτης
αυτή τη στιγμή δεν είναι συνδεδεμέν. Δεν έχει γράψει κανένα μήνυμα.

02-08-21

15:54
η τελευταια μεθοδολογια που διδαχτηκα ηταν τα ορια στο απειρο αλλα αυτο επεσε στο τελικο διαγωνισμαοι καλοι μαθητες γραφουν βαση απο που και ως που??ποιος το λεει αυτο??μην ακους κανεναν.προπονηση θελουν τα μαθηματικα.διαβασε τις μεθολογιες ολες,κατανοησε καλα τη θεωρια και δεν υπαρχει περιπτωση να μην γραψεις καλα.δεν ειναι διαγωνισμος μαθηματικης εταιρειας!!το θεμα που σου λυσα με τα ορια εχετε κανει τις ασυμπτωτες??αν τις εχετε κανει τοτε μην αγχωνεσαι που δεν το λυσες οπως εγω γτ ειναι ολιγον extreme τροπος.με ασυμπτωτες ειναι εφαρμογη της θεωριας.
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.965 μηνύματα.

02-08-21

16:01
αρα λογικα ειστε στις αρχες και δεν εχετε κανει ασυμπτωτους που ειναι στο κεφαλαιο μετα το de l hospital.κακως σας εβαλε τετοια ασκηση γτ ηθελε αυτο το κολπο που οκ δεν το λες και το πιο απλο να το σκεφτεις αν δεν ξερεις ασυμπτωτους.μην απογοητευεσαι.τη δευτερη ερωτηση την κατανοησες?αυτη ειναι πιο σημαντικη σε σχεση με την πρωτηη τελευταια μεθοδολογια που διδαχτηκα ηταν τα ορια στο απειρο αλλα αυτο επεσε στο τελικο διαγωνισμα
Guest 954356
Επισκέπτης
αυτή τη στιγμή δεν είναι συνδεδεμέν. Δεν έχει γράψει κανένα μήνυμα.

02-08-21

16:14
ναι και πραγματικα ευχαριστω πολυ αν και το ελυσα αφου το ανεβασα. Την πρωτη ακομα να την καταλαβω δυστυχως. ειλικρινα ησασταν μεγαλη βοηθεια! και παλι ευχαριστω!
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 1 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 49 μέλη διάβασαν αυτό το θέμα:
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki