Γεια!
Ήρθε η ώρα της εξεταστικής κ συνειδητοποιώ ότι μου βγαίνουν λάθος οι ασκήσεις στην Γραμμική Άλγεβρα.Παραθέτω μια μαζί με την λύση που της έδωσα για να μου πει κ κάποιος άλλος τη γνώμη του.
Άσκηση :
Έστω τα σημεία Ρ(1,1,1) και Q(0,2,1). Από το σημείο Μ που είναι μέσο του ευθ.τμήματος PQ φέρνουμε επίπεδο κάθετο στo PQ και στην ευθεία που αυτό τέμνει το ΧΟΥ θεωρούμε το σημείο R που έχει x=0. Να βρεθεί η εξίσωση του επιπέδου (Π) που περνά από το P και είναι κάθετο στο
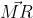
. Να δείξετε ότι το (Π) περιέχει κ το σημείο Q.
Προσπάθεια απάντησης :
Προκειμένου να βρω την εξίσωση του ζητούμενου επιπέδου αναζητώ αρχικά το σημείο Μ,στη συνέχεια την εξίσωση του επιπέδου (Α) το οποίο περιέχει το σημείο Μ κ είναι κάθετο στο
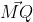
.Μετά αφού έχω την εξίσωση του επιπέδου (Α) μπορώ να βρω τις συντεταγμένες του R αφού R
)
,στη συνέχεια να υπολογίσω το
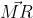
που είναι κάθετο στο ζητούμενο επίπεδο κ άρα τελικά να βρω την εξίσωση του (Π).
Παρατηρώ ότι αφού Μ μέσο του PQ ισχύει :
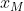
=1/2 ,
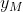
=3/2 ,
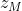
=1
Άρα τελικά Μ(1/2 , 3/2 , 1).
Εύρεση της εξίσωσης του (Α) : Ισχύει ότι
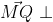
(Α).
Παρατηρώ
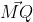
= (0-1/2 , 2-3/2 , 1-1) δηλαδή
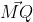
= ( -1/2 , 1/2 , 0)
Έτσι αφού έχουμε ένα σημείο, το Μ, που ανήκει στο (Α) και ένα διάνυσμα κάθετο στο (Α) η καρτεσιανή εξίσωση του επιπέδου (Α) είναι
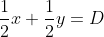
όπου
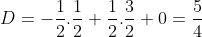
.
Άρα το (Α) έχει εξίσωση
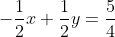
(το ότι χάθηκε το z τι σημαίνει;;

)
To R ανήκει στο (Α) άρα οι συνταγμένες του πρέπει να επαληθέυουν την εξίσωση του επιπέδου. Έτσι
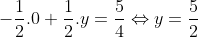
.
Άρα
)
.
Υπολογίζω το
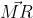
.
 )
δηλαδή
 )
Βρίσκω την εξίσωση του επιπέδου (Π) αφού έχω το σημείο Ρ(1,1,1) που ανήκει στο (Π) και το
)
.
Καρτεσιανή εξίσωση επιπέδου :
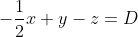
όπου D = -1/2.
Άρα η εξίσωση του (Π) είναι
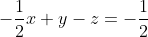
.
Ελέγχω αν Q(0,2,1) είναι σημείο του (Π) κ τελικά οι συντεταγμένες του δεν επαληθεύουν την εξίσωση του επιπέδου....
