ΘΕΜΑ 1ο
Α. Εφόσον A και Β ασυμβίβαστα, τότε

δηλαδή τα Α και Β δεν έχουν κοινά στοιχεία (
=0\Rightarrow P\left( A\bigcap B\right)=0)
)
Αν Ω είναι ο δειγματικός χώρος του πειράματος τύχης και περιέχει N(Ω) απλά ενδεχόμενα και Ν(Α), N(B) είναι τα στοιχεία του Ω πυ περιέχουν τα ενδεχόμενα Α και Β τότε
Συνεπώς
=N(A)+N(B)\Rightarrow \frac{N\left(A\bigcup B \right)}{N(\Omega) }=\frac{N(A)}{N(\Omega) }+\frac{N(B)}{N(\Omega) }\Rightarrow P\left(A\bigcup B \right)=P(A)+P(B))
(Μαζί με την απόδειξη διάγραμμα Venn)
Β. Ως συχνότητα
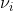
της παρατήρησης

, ορίζεται ο φυσικός αριθμός που δείχνει πόσες φορές εμφανίστηκε η παρατήρηση

της μεταβλητής X στο δείγμα μεγέθους ν.
Σχετική συχνότητα
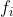
της παρατήρησης

, ορίζεται το πηλικό της συχνότητας
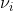
προς το μέγεθος του δείγματος ν και ανήκει στο διάστημα [0,1].
Γ. α) Λάθος, β) Σωστό, γ) Λάθος, δ) Σωστό, ε) Σωστό
ΘΕΜΑ 2ο
A. 
όπου n=4 και

=4{\nu }_{2}+52)

Επομένως
 B.
B. 
}^{2}=6{}^{.}{\left(2-4 \right)}^{2}+7{}^{.}{\left(3-4 \right)}^{2}+3{}^{.}{\left(5-4 \right)}^{2}+4{}^{.}{\left(8-4 \right)}^{2}=24+7+3+64=98)
}^{2}}{\sum_{i=1}^{n}{\nu }_{i}}=\frac{\sum_{i=1}^{n}{\nu }_{i}{\left({x}_{i}-\bar{x} \right)}^{2}}{\nu }=\frac{98}{20}=\frac{49}{10}=4,9) Γ.
Γ. 
 ΘΕΜΑ 3ο
α.
ΘΕΜΑ 3ο
α. ={x}^{3}-6{x}^{2}+\alpha x-7<br />
)
Η f είναι συνεχής και άπειρες φορές παραγωγίσιμη στο R ως πολυωνυμική. Υπολογίζεται η πρώτη και η δεύτερη παράγωγος.
=3{x}^{2}-12x+\alpha)
=6x-12=6(x-2))
Θεωρούμε την συνάρτηση
=2f''(x)+f'(x)+15-3{x}^{2})
η οποία σύμφωνα με την εκφώνηση είναι σταθερή και
=0)
για κάθε x στο R.
=2f''(x)+f'(x)+15-3{x}^{2}=12x-24+3{x}^{2}-12x+\alpha +15-3{x}^{2}=\alpha -9)
Για να ισχύει
=0)
για κάθε x στο R πρέπει

Άρα

.
β. ={x}^{3}-6{x}^{2}+9x-7)
=3{x}^{2}-12x+9=3\left( {x}^{2}-4x+3\right)=3\left( {x}^{2}-4x+4-1\right)=3[({x}^{2}-4x+4)-1]=3[\left( {x-2}\right)^{2}-1]=3(x-2-1)(x-2+1)=3(x-3)(x-1))
για κάθε x στο R.
}{{x}^{2}-1}=\lim_{x\rightarrow 1}\frac{3(x-3)(x-1)}{(x-1)(x+1)}=\lim_{x\rightarrow 1}\frac{3(x-3)}{x+1}=\frac{3(1-3)}{1+1}=\frac{3{}^{.}(-2)}{2}=\frac{-6}{2}=-3) γ.
γ. Δύο μη κατακόρυφες ευθείες είναι παράλληλες αν και μόνο αν έχουν τον ίδιο συντελεστή διεύθυνσης. Ο συντελεστής διεύθυνσης της εφαπτομένης της γραφικής παράστασης της f στο σημείο
 \right))
ισούται με την παράγωγο στης f στο
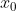
και συνεπώς έχει εξίσωση της μορφής:
(ε) :
x+\beta )
Η εφαπτομένη (ε) διέρχεται από το
 \right))
, οπότε:
=f'\left({x}_{0} \right){x}_{0}+\beta \Rightarrow \beta =f\left({x}_{0} \right)-f'\left({x}_{0} \right){x}_{0})
Συνεπώς η εξίσωση της εφαπτομένης (ε) στο
 \right))
γινεται
x+f\left({x}_{0} \right)-{x}_{0}f'\left({x}_{0} \right))
Η ευθεία (δ) με εξίσωση y=-3x έχει συντελεστή διεύθυνσης λ=-3. Επομένως η εφαπτομένη της γραφικής παράστασης της f στο
 \right))
η οποία είναι παράλληλη στην ευθεία (δ) έχει συντελεστή διεύθυνσης
=\lambda =-3)
. Έχουμε
=-3\Rightarrow 3{{x}_{0}}^{2}-12{x}_{0}+9=-3\Rightarrow 3{{x}_{0}}^{2}-12{x}_{0}+12=0\Rightarrow {{x}_{0}}^{2}-4{x}_{0}+4=0\Rightarrow ({{x}_{0}-2})^{2}=0\Rightarrow {x}_{0}-2=0\Rightarrow {x}_{0}=2)
={2}^{3}-6{}^{.}{2}^{2}+9{}^{.}2-7=8-24+18-7=-16+11=-5)
=3{}^{.}{2}^{2}-12{}^{.}2+9=12-24+9=-12+9=-3)
Αντικαθιστώντας στην εξίσωση της εφαπτομένης για

έχουμε
x+f(2)-2f'(2)\Rightarrow y=-3x-5-2{}^{.}(-3)\Rightarrow y=-3x+1)
Η μοναδική εφαπτομένη της γραφικής παράστασης της f που είναι παράλληλη στην ευθεία y=-3x έχει εξίσωση y=-3x+1.
ΘΕΜΑ 4ο
Α. α)
=lnx-\frac{x}{2}+{\lambda }^{2}-6\lambda +2)
f συνεχής και παραγωγίσιμη στο
)
με παράγωγο
=\frac{1}{x}-\frac{1}{2}=\frac{2-x}{2x})
για x>0.
=0\Rightarrow x-2=0\Rightarrow x=2)
Η f είναι συνεχής στο (0,2], παραγωγίσιμη στο (0,2) και ισχύει f΄(x)>0 για κάθε x στο (0,2). Άρα η f είναι γνησίως αύξουσα στο (0,2]
Η f είναι συνεχής στο
)
, παραγωγίσιμη στο
)
και ισχύει f΄(x)>0 για κάθε x στο
)
. Άρα η f είναι γνησίως αύξουσα στο
)
.
β) f γνησίως αύξουσα στο (0,2] και γνησίως φθίνουσα στο
)
. Άρα η f παρουσιάζει ολικό μέγιστο στο

με τιμή
={\lambda }^{2}-6\lambda +1+ln2)
Δηλαδή
\leq f(2))
για κάθε
) Β.
Β. α) Η f είναι γνησίως φθίνουσα στο
)
.
Συνεπώς
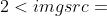
<4<5<8\Rightarrow f(2)>f(3)>f(4)>f(5)>f(8)" />
Ταξινομούνται οι παρατηρήσεις της μεταβλητής X κατά αύξουσα σειρά:
, {x}_{2}=f(5), {x}_{3}=f(4), {x}_{4}=f(3), {x}_{5}=f(2))
={\lambda }^{2}-6\lambda+1+ln2)
={\lambda }^{2}-6\lambda+\frac{1}{2}+ln3)
={\lambda }^{2}-6\lambda+ln4={\lambda }^{2}-6\lambda+ln{2}^{2}={\lambda }^{2}-6\lambda+2ln2)
={\lambda }^{2}-6\lambda-\frac{1}{2}+ln5)
={\lambda }^{2}-6\lambda-2+ln8={\lambda }^{2}-6\lambda-2+ln{2}^{3}={\lambda }^{2}-6\lambda-2+3ln2)
-f(8)=3-2ln2=3-ln{2}^{2}=3-ln4=3+ln{4}^{-1}=3+ln\frac{1}{4})
Ο αριθμός των παρατωρήσεων είναι
\Rightarrow \delta =ln4+{\lambda }^{2}-6\lambda )
β)


Θεωρώ το πολυώνυμο
={\lambda }^{2}-6\lambda +5)
Υπολογίζω την διακρίνουσα της εξίσωσης
=0)


Ισχύει
<0)
όταν

Συνεπώς το ενδεχόμενο Α περιλαμβάνει τα εξής απλά ενδεχόμενα

Όλα τα απλά ενδεχόμενα του δειγματικού χώρου Ω είναι ισοπίθανα, οπότε
=P(2)=P(3)=...=P(100)=P=\frac{1}{100})
Υπολογίζεται η P(A):
=P(2)+P(3)+P(4)=P+P+P=3P=\frac{3}{100})
Άρα η πιθανότητα του ενδεχομένου A είναι
=\frac{3}{100})
.