Ασκήσεις και απορίες πάνω στη Θεωρία Πιθανοτήτων

[bovid19]

Δεν βρήκα αντίστοιχο θέμα οπότε παίρνω την πρωτοβουλία και το δημιουργώ. Ο σκοπός είναι να συμμετέχουμε σε υψηλού επιπέδου συζητήσεις πάνω στη Θ.Π. και να λύνουμε διάφορες απορίες/ασκήσεις..

Ας κόψω την κορδέλα λοιπόν με την πρώτη άσκηση σε ένα θέμα που ξέρω ότι θα είναι ενεργό για δεκαετίες ολόκληρες (not) :

Έστω πείραμα στο οποίο ρίχνουμε δυο ζάρια και καταγράφουμε το αποτέλεσμα, πόσα διαφορετικά ενδεχόμενα E υπάρχουν τέτοια ώστε

 

[Samael]

Μήπως εννοείς πόσα διαφορετικά αποτελέσματα ικανοποιούν το ενδεχόμενο Ε ; Λεπτή αλλά σημαντική η διαφορά, οπότε ρωτάω μήπως και στην διατύπωση το εξέφρασες αλλιώς.

 

[bovid19]

Μήπως εννοείς πόσα διαφορετικά αποτελέσματα ικανοποιούν το ενδεχόμενο Ε ; Λεπτή αλλά σημαντική η διαφορά, οπότε ρωτάω μήπως και στην διατύπωση το εξέφρασες αλλιώς.

Ουσιαστικά ρωτάω πόσα είναι τα ενδεχόμενα Ε που ικανοποιούν τη δεδομένη σχέση. Άμα θες σβήσε το "διαφορετικά" γιατί μάλλον προκαλεί σύγχυση.

 

[Samael]

Ουσιαστικά ρωτάω πόσα είναι τα ενδεχόμενα Ε που ικανοποιούν τη δεδομένη σχέση. Άμα θες σβήσε το "διαφορετικά" γιατί μάλλον προκαλεί σύγχυση.

Οτι είναι διαφορετικά είναι σίγουρο,για το πλήθος προφανώς το έγραψες.
Τέλος πάντων,θα πω 8,και εαν έχω καταλάβει σωστά την εκφώνηση λογικά θα πέφτω μέσα. Εαν δεν είναι τόσο,απλά πες το χωρίς να χρειαστεί να "μαρτυρήσεις" την απάντηση σε περίπτωση που κάποιος άλλος θέλει να δοκιμάσει .

Πολύ καλή πρωτοβουλία να φτιάξεις το θέμα σε κάθε περίπτωση .

 

[Guest 190013]

Το πείραμα με τα 2 ζάρια έχει 36 στοιχειώδη ενδεχόμενα. Δεδομένου ότι το πρόβλημα είναι διακριτό σε αυτά τα ενδεχόμενα και με βάση τον κλασικό ορισμό της πιθανότητας, ψάχνουμε όλα τα δυνατά sets (events) που από τα 36 αυτά simple events θα ικανοποιούνται τα 8 ( = 2/9). Συνεπώς θα υπάρχουν (36 8) τέτοια events, νομίζω βγαίνει πάνω από 30 εκατομμύρια.

 

[bovid19]

Ωραίος, ψηθείτε και οι υπόλοιποι βάλτε τίποτα.

Οτι είναι διαφορετικά είναι σίγουρο,για το πλήθος προφανώς το έγραψες.
Τέλος πάντων,θα πω 8,και εαν έχω καταλάβει σωστά την εκφώνηση λογικά θα πέφτω μέσα. Εαν δεν είναι τόσο,απλά πες το χωρίς να χρειαστεί να "μαρτυρήσεις" την απάντηση σε περίπτωση που κάποιος άλλος θέλει να δοκιμάσει .

Πολύ καλή πρωτοβουλία να φτιάξεις το θέμα σε κάθε περίπτωση .

Με πρόλαβαν πριν σου απαντήσω, μην κοιτάξεις πάνω :Ρ

 

[Guest 190013]

Okay take one:

Ο @bovid19, εγώ κι άλλα 8 άτομα καθόμαστε σε ένα κυκλικό τραπέζι. Με πόσους τρόπους μπορούμε να καθίσουμε στο τραπέζι δεδομένου ότι ανάμεσα σε μένα και τον @bovid19 πρέπει να παρεμβάλλεται ακριβώς ένα άτομο, για να μη τσακωθούμε πολιτικά;

 

[Samael]

Ωραίος, ψηθείτε και οι υπόλοιποι βάλτε τίποτα.


Με πρόλαβαν πριν σου απαντήσω, μην κοιτάξεις πάνω :Ρ

Χαχαχα,πέτυχα την αρχή μα έχασα το τέλος .
Του Κλεάνθη μου φαίνεται πιο πλήρης ο συλλογισμός .

 

[bovid19]

Okay take one:

Ο @bovid19, εγώ κι άλλα 8 άτομα καθόμαστε σε ένα κυκλικό τραπέζι. Με πόσους τρόπους μπορούμε να καθίσουμε στο τραπέζι δεδομένου ότι ανάμεσα σε μένα και τον @bovid19 πρέπει να παρεμβάλλεται ακριβώς ένα άτομο, για να μη τσακωθούμε πολιτικά;

Spoiler

Διακρίνουμε τα εξής βήματα: 1) Επιλέγεις θέση (10 τρόποι) (υποθέτω 10 θέσεις)
2) Επιλέγω θέση (2 τρόποι αν πρέπει να έχουμε 1 κενή θέση ανάμεσα μας)
3) Οι υπόλοιποι 8 επιλέγουν θέσεις (8!)

Σύνολο = 2*10*8! αλλά έχεις πει ότι είναι κυκλικό το τραπέζι άρα κάθε συνδυασμός έχει άλλους 9 (σύνολο 10) παρόμοιους μέσω περιστροφών. Άρα πρέπει να είναι 2*8! οι τρόποι που μπορούμε να καθίσουμε για να μην γίνει Τατσόπουλος-Σταυρίδης η φάση. Αν κάνω λάθος απλά πες το μονολεκτικά, όχι σπόιλερς.

 

[Guest 190013]

Ας είναι το λαμπάκι ένδειξη σωστού. Εντωμεταξύ το έγραψα χωρίς να έχω λύση αλλά το έλυσα και βγάζω the same so ok.

 

[Μάρκος Βασίλης]

Ήμουν ανάμεσα σε δύο για αρχή, θα βάλω το πιο γνωστό και κλασσικό - και αυτό για το οποίο είμαι σίγουρος για την απάντηση :Ρ

Παίζουμε το εξής παιχνίδι απέναντι στον Elon Musk - ένα πρακτικά άπειρα πλούσιο αντίπαλο:
1. Ο Elon στρίβει ένα νόμισμα το οποίο με πιθανότητα p φέρνει κορώνα - και με 1-p γράμματα. Ας υποθέσουμε ότι 0<p<1.
2. Αν έρθει κορώνα, κερδίζουμε από τον Elon ένα ευρώ.
3. Αν έρθει γράμματα, χάνουμε ένα ευρώ - το τσεπώνει ο Elon.
4. Επαναλαμβάνουμε τα παραπάνω μέχρι να χρεοκοπήσουμε.

Υποθέτουμε τώρα ότι έχουμε ένα αρχικό κεφάλαιο Κ ευρώ - Κ ακέραιος. Ποια είναι η πιθανότητα να τερματίσει το παραπάνω παιχνίδι - δηλαδή να χρεοκοπήσουμε;

Είναι πολύ πιο απλό από ό,τι φαίνεται...

 

[Samael]

Ήμουν ανάμεσα σε δύο για αρχή, θα βάλω το πιο γνωστό και κλασσικό - και αυτό για το οποίο είμαι σίγουρος για την απάντηση :Ρ

Παίζουμε το εξής παιχνίδι απέναντι στον Elon Musk - ένα πρακτικά άπειρα πλούσιο αντίπαλο:
1. Ο Elon στρίβει ένα νόμισμα το οποίο με πιθανότητα p φέρνει κορώνα - και με 1-p γράμματα. Ας υποθέσουμε ότι 0<p<1.
2. Αν έρθει κορώνα, κερδίζουμε από τον Elon ένα ευρώ.
3. Αν έρθει γράμματα, χάνουμε ένα ευρώ - το τσεπώνει ο Elon.
4. Επαναλαμβάνουμε τα παραπάνω μέχρι να χρεοκοπήσουμε.

Υποθέτουμε τώρα ότι έχουμε ένα αρχικό κεφάλαιο Κ ευρώ - Κ ακέραιος. Ποια είναι η πιθανότητα να τερματίσει το παραπάνω παιχνίδι - δηλαδή να χρεοκοπήσουμε;

Είναι πολύ πιο απλό από ό,τι φαίνεται...

Θα μαντέψω οτι εξαρτάται απο το ποιόν "ευνοεί" η πιθανότητα p.
Ας πούμε εαν 0.5<p<1 τότε δεν θα χρεοκοπήσουμε ποτέ.
Εαν όμως 0<p<0.5 τότε θα χρεοκοπήσουμε κάποια στιγμή όσο συνεχίζει το παιχνίδι.
Και εαν p = 0.5 τότε μάλλον το παιχνίδι δεν θα τερματίσει ποτέ.

Έτσι το βλέπω πρακτικά για ένα μεγάλο K.

Τώρα θεωρητικά η αλήθεια είναι οτι θα μπορούσε κάποιος να ήταν τόσο άτυχος που να ρίξει K φορές και να έρθει κορώνα απανωτά οπότε να χάσει . Λογικά όμως κάτι τέτοιο όσο το K μεγαλώνει δεν παίζει τόσο.Δώσε μας τα φώτα σου.

Σωστός ;

 

[bovid19]

Αν p=1/2 έχουμε τυχαίο περίπατο οπότε σίγουρα κάποια στιγμή θα χάσουμε. Για διαφορετικό p το ψάχνω ακόμη.

 

[Samael]

Θα προτείνω και κάτι ακόμα που η διαίσθηση μου μου λέει οτι είναι καλή μαντεψιά βάσει του τελευταίου μου προβληματισμού στην προηγούμενη μαντεψιά... Μήπως παίζει και το οτι είναι σίγουρο οτι κάποια στιγμή θα χρεοκοπήσουμε ανεξάρτητα του p όσο αυτό είναι 0<p<1 ;

 

[Guest 190013]

Spoiler

Αν p=1/2 έχουμε τυχαίο περίπατο οπότε σίγουρα κάποια στιγμή θα χάσουμε. Για διαφορετικό p το ψάχνω ακόμη.

Διαισθητικά, αφού ο Elon έχει άπειρο κεφάλαιο και ένα δίκαιο νόμισμα (p=1/2), μπορεί να παίξει μαζί μας όσο γουστάρει μέχρι να μας κάνει να χάσουμε. Ισχύει συνεπώς αυτό που λες. Και προφανώς θα ισχύει ακόμα περισσότερο αν p<1/2 οπότε και θα το κάνει γρηγορότερα. Το ερώτημα είναι τι γίνεται αν p>1/2. Εδώ υπάρχει μια μη τετριμμένη πιθανότητα να χάσουμε, νομίζω (1-p)/p. Δε παίρνω και όρκο αλλά διαισθητικά μου κάνει, πχ αν p=1 η πιθανότητα μηδενίζεται όπως πρέπει. Η απόδειξη λογικά βαραίνει από μαθηματική άποψη οπότε δε ξέρω αν ο @Μάρκος Βασίλης έχει άλλη προσέγγιση στο μυαλό του. Το ενδιαφέρον της υπόθεσης, που το είπα διαισθητικά αλλά προκύπτει και μαθηματικά, είναι ότι ενώ στον τυχαίο περίπατο χάνουμε σίγουρα, ο expected χρόνος για να συμβεί αυτό απειρίζεται.

 

[bovid19]

@Μάρκος Βασίλης Ρίχ'το. Δεν μου βγαίνει με τίποτα.

Spoiler

Spoiler

Διαισθητικά, αφού ο Elon έχει άπειρο κεφάλαιο και ένα δίκαιο νόμισμα (p=1/2), μπορεί να παίξει μαζί μας όσο γουστάρει μέχρι να μας κάνει να χάσουμε. Ισχύει συνεπώς αυτό που λες. Και προφανώς θα ισχύει ακόμα περισσότερο αν p<1/2 οπότε και θα το κάνει γρηγορότερα. Το ερώτημα είναι τι γίνεται αν p>1/2. Εδώ υπάρχει μια μη τετριμμένη πιθανότητα να χάσουμε, νομίζω (1-p)/p. Δε παίρνω και όρκο αλλά διαισθητικά μου κάνει, πχ αν p=1 η πιθανότητα μηδενίζεται όπως πρέπει. Η απόδειξη λογικά βαραίνει από μαθηματική άποψη οπότε δε ξέρω αν ο @Μάρκος Βασίλης έχει άλλη προσέγγιση στο μυαλό του. Το ενδιαφέρον της υπόθεσης, που το είπα διαισθητικά αλλά προκύπτει και μαθηματικά, είναι ότι ενώ στον τυχαίο περίπατο χάνουμε σίγουρα, ο expected χρόνος για να συμβεί αυτό απειρίζεται.

Το Γκουγκλ λέει ότι είναι (q/p)^K. Αλλά όντως δεν είναι καθόλου τετριμμένο.

 

[Μάρκος Βασίλης]

Λοιπόν, αρχικά, το πρόβλημα όντως μπορεί να μοντελοποιηθεί γενικά ως ένας τυχαίος περίπατος. Για την ακρίβεια, τελικά, η απάντηση είναι:
1. για p<=1/2 χρεοκοπούμε με πιθανότητα 1 - λογικό αυτό.
2. για p>1/2 χρεοκοπούμε με πιθανότητα ((1-p)/p)^K

Η αλήθεια είναι ότι υπάρχει μία κουραστική λύση με πολύ μέτρημα - που δεν τη θυμάμαι απ'έξω :Ρ - και μία πιο συμπαθητική λύση που βρίσκει αυτό που διατηρείται αναλλοίωτο στο πρόβλημά μας. Στη περίπτωσή μας, αυτό είναι η πιθανότητα τελικά να χάσουμε ένα ευρώ. Λέγοντας τελικά εννοούμε την πιθανότητα μετά από κάποιες κινήσεις να βρεθούμε, τελικά, με ένα ευρώ λιγότερο για πρώτη φορά. Αυτό τώρα μπορεί να γίνει π.χ. κερδίζοντας και χάνοντας εναλλάξ πέντε φορές και μετά χάνοντας άλλη μία ή χάνοντας απευθείας μία φορά κ.λπ. Ας πούμε r αυτήν την πιθανότητα.

Το να πτωχεύσουμε, λοιπόν, συνίσταται στο να χάσουμε Κ φορές από ένα ευρώ τελικά. Θεωρώντας με ασφάλεια ότι το r είναι ανεξάρτητο από το αρχικό μας κεφάλαιο μπορούμε να δούμε από το Θεώρημα Ολικής Πιθανότητας ότι:

Δηλαδή, η πιθανότητα να χάσουμε τα Κ ευρώ μας είναι η πιθανότητα να χάσουμε K+1 ευρώ δεδομένου ότι κερδίζουμε στην αρχή επί την πιθανότητα να κερδίσουμε τον πρώτο γύρο + την πιθανότητα να χάσουμε K-1 ευρώ δεδομένου ότι χάνουμε στην αρχή δεδομένου ότι χάνουμε τον πρώτο γύρο.

Τώρα από πάνω βγάζουμε τρεις τιμές για το r: 0, 1 και (1-p)/p.

Για p<=1/2 απορρίπτεται η τρίτη, ενώ οι άλλες δύο, όταν δεν μας χρειάζονται, μπορούν να απορριφθούν με νόμους των μεγάλων αριθμών -τώρα, η μία νομίζω ότι βγαίνει εκτός κι από Bore-Cantelli ή Markov ή κάποια άλλη διάσημη ανισότητα, αλλά δεν το βλέπω αυτή τη στιγμή. Επομένως, έχουμε τη ζητούμενη πιθανότητα r^K όπως παραπάνω.

 

[Guest 190013]

Follow up για όσους δεν έχουν δει το spoiler μου παραπάνω (ή και για όσους το έχουν δει, δείξτε το μαθηματικά): Στην περίπτωση p=1/2 που χάνουμε με πιθανότητα 1 βρείτε μεσοσταθμικά σε πόσους γύρους θα χάσουμε. Θα σας βοηθήσει το παραπάνω μήνυμα.

 

[bovid19]

Πώς το έκανες; Με την ίδια λογική του @Μάρκος Βασίλης έκανα όπου 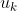οι αναμενόμενοι γύροι μέχρι να χάσουμε δεδομένου ότι έχουμε κεφάλαιο k. Το παραπάνω δίνει 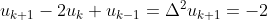που είναι μία δευτεροβάθμια εξίσωση διαφορών με διπλή ρίζα 1. Η γενική λύση βγαίνει 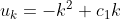και δεν έχω ιδέα τι να κάνω με αυτό. Ενώ για 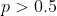η ίδια διαδικασία μου δίνει
όπου αν πάρω το όριο 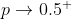βγαίνει 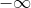και δεν ξέρω αν βγάζει νόημα αυτό. Αν βαριέσαι δώσε μια συνοπτική λύση χωρίς να δείχνεις τα ενδιάμεσα μαθηματικά.

 

[Guest 190013]

Καλά το πας γενικά. Για πιο εύκολα τσέκαρε πώς βγαίνει η αναδρομική στην βάση k=1.