Naki_Marina
Νεοφερμένο μέλος


"Αν έχει κίνηση, ο χρόνος οδήγησης μέχρι την εργασία του Κώστα είναι ομοιόμορφα κατανεμημένος στο [25, 50], ενώ όταν δεν έχει κίνηση, ο χρόνος οδήγησης είναι ομοιόμορφα κατανεμημένος στο [20, 30].
Η πιθανότητα κίνησης στην πόλη του Κώστα είναι 55%.
1) Προσδιορίστε τη συνάρτηση πυκνότητας πιθανότητας του χρόνου οδήγησης μίας τυχαίας μέρας
2) Ποια η πιθανότητα ο μέσος χρόνος οδήγησης προς την εταιρεία μας μετά από 50 μέρες να είναι μεγαλύτερος από 31 λεπτά;"
Λοιπόν, όσον αφορά το πρώτο ερώτημα, είμαι πολύ μπερδεμένη γιατί τα δύο σύμβολα έχουν κοινές τιμές. Στην αρχή, σκέφτηκα η συνάρτηση f(x) να έχει 4 περιπτώσεις (c1 για 30<χ<50, c2 για 20<χ<25, c3 για 25<χ< 30 και 0 για οποιαδήποτε άλλη τιμή) αλλά έχω σπάσει το κεφάλι μου για το c3... Πρέπει να το ενσωματώσω σε μία από τις άλλες, ή έχει εντελώς διαφορετική τιμή;
Και για το δεύτερο ερώτημα, βρήκα κάπου ότι πρέπει να το λύσω χρησιμοποιώντας μέσο, διακύμανση και κανονική κατανομή, αλλά δεν ξέρω πως ακριβώς πρέπει να εκφράσω το πέρας των 50 ημερών.
Γενικά αυτές είναι οι σκέψεις μου, θα ήθελα όμως να ακούσω πως θα το λύνατε και εσείς, και να μου τονίσετε αν έχω καταλάβει κάτι λάθος και για αυτό δεν βρίσκω κατάλληλες λύσεις

Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
eukleidhs1821
Διάσημο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Naki_Marina
Νεοφερμένο μέλος


Εντάξει, χαίρομαι που δεν είναι περίεργη η άσκηση μόνο σε μένα! Από τι έχω καταλάβει, είναι τα λεπτά που κάνει ο Κώστας για να φτάσει στη δουλειά τουκαταρχην ειναι οτι να ναι η εκφωνηση.τα κλειστα διαστηματα τι εκφραζουν?
Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
eukleidhs1821
Διάσημο μέλος


απλα πεταει ενα χρονος οδηγησης ετσι ξερα.γραψε τι ειναι αυτα??min,ωρες,μερες!!τεσπα λεπτομερειες αυτα αλλα ποσο της πλακας παιδεια εχουμε φαινεται και απο τις εκφωνησεις
Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Naki_Marina
Νεοφερμένο μέλος


Με αυτό τον τρόπο, το κοινό διάστημα, το [25,30], δεν το υπολογίζω δύο φορές? Φυσικά και εγώ δεν είμαι σίγουρη απλά μαρέσει το brainstorming!λοιπον κατι ψιλοκαταλαβα.Ουσιαστικα εχεις 2 περιπτωσεις.Αν εχει κινηση ο δρομος η πιθανοτητα ειναι 55% και ο χρονος καταναμεται ομοιομορφα στο [25,50] δηλαδη η πιθανοτητα ειναι (1/50-25)*0.55.Αν δεν εχει κινηση ο δρομος η πιθανοτητα προφανως ειναι 45% οποτε η πιθανοτητα να καταναμεται ομοιομορφα στο [20,30] ειναι (1/30-20)*0.45.Αρα η πυκνοτητα πιθανοτητας προκυπτει απο το αθροισμα αυτων των 2 πιθανοτητων.με επιφυλαξη φυσικα

Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
eukleidhs1821
Διάσημο μέλος


τι ειναι το brainstroming?οχι δεν ειναι αλληλοεπικαλυπτομενα αυτα τα διαστηματα γτ μιλας σε διαφορετικες περιπτωσεις.στη μια περιπτωση που δεν εχει μποτιλιαρισμα ο χρονος ειναι ταδε αν δεν εχει μποτιλιαρισμα ο χρονος ειναι ταδε.Διαφορετικα εντελως συνολα,για αυτο κανεις τον απλο προσθετικο νομο πιθανοτητων.!Με αυτό τον τρόπο, το κοινό διάστημα, το [25,30], δεν το υπολογίζω δύο φορές? Φυσικά και εγώ δεν είμαι σίγουρη απλά μαρέσει το brainstorming!
το δευτερο ερωτημα εφοσον βρηκες για κανονικη κατανομη εχει φουστιτσα οτι πρεπει να εφαρμοσεις κεντρικο οριακο θεωρμα διοτι σου λεει μετα απο 51 ημερες αρα να τεινει στο απειρο!!
Θυμισε μου λιγο τυπο μεσης τιμης ομοιομορφης και διασπορας ομοιομορφης!Ή βρες το στο google.Σκυλοβαριεμαι να κατσω να κανω το ολοκληρωμα για εναν ετοιμο τυπο θεωριας
Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Naki_Marina
Νεοφερμένο μέλος


Ααα τίποτα, είναι η ανταλλαγή ιδεών! Χμμ κατάλαβα... Δηλαδή θεωρείς ότι η συνάρτηση δεν πρέπει να είναι διακλάδωση, αλλά ένας αριθμός? Πίστευα ότι θα έμοιαζε πιο πολύ με ένα παράδειγμα που είχαμε κάνει, το οποίο έχει να κάνει με την πιθανότητα βροχής και έπρεπε να την λύσουμε έτσι την συνάρτηση:τι ειναι το brainstroming?οχι δεν ειναι αλληλοεπικαλυπτομενα αυτα τα διαστηματα γτ μιλας σε διαφορετικες περιπτωσεις.στη μια περιπτωση που δεν εχει μποτιλιαρισμα ο χρονος ειναι ταδε αν δεν εχει μποτιλιαρισμα ο χρονος ειναι ταδε.Διαφορετικα εντελως συνολα,για αυτο κανεις τον απλο προσθετικο νομο πιθανοτητων.!
Απλά εδώ πέρα δεν συμπίπτουν τα σύνολα!
Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
eukleidhs1821
Διάσημο μέλος


εδω ομως ειναι στο ιδιο συνολο δεδομενων!!στο παραδειγμα το διαχωριζει.Επισης τα c1,c2 στο παραδειγμα ειναι 1/5=0.2.Γτ τα γραφει ετσι?Ααα τίποτα, είναι η ανταλλαγή ιδεών! Χμμ κατάλαβα... Δηλαδή θεωρείς ότι η συνάρτηση δεν πρέπει να είναι διακλάδωση, αλλά ένας αριθμός? Πίστευα ότι θα έμοιαζε πιο πολύ με ένα παράδειγμα που είχαμε κάνει, το οποίο έχει να κάνει με την πιθανότητα βροχής και έπρεπε να την λύσουμε έτσι την συνάρτηση:
View attachment 69817
Απλά εδώ πέρα δεν συμπίπτουν τα σύνολα!
Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Naki_Marina
Νεοφερμένο μέλος


Όσα γνωρίζεις εσύ, τόσα γνωρίζω και εγώ! Αααα κατάλαβα κατάλαβα τι εννοείς! Απλά για κάποιο λόγο ήμουν πεπεισμένη ότι πρέπει να το λύσω με τον ίδιο τρόπο!εδω ομως ειναι στο ιδιο συνολο δεδομενων!!στο παραδειγμα το διαχωριζει.Επισης τα c1,c2 στο παραδειγμα ειναι 1/5=0.2.Γτ τα γραφει ετσι?
Οοοο ναι το είχα ξεχάσει εντελώς το ΚΟΘ! Η μέση τιμή της ομοιόμορφης είναι E[x]=(β+α)/2 και η διακύμανση Var(x)=(β-α)^2/12
Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Samael
Τιμώμενο Μέλος


f(x) =
9/200 , 20 < x < 25
67/1000 , 25 < x < 30
11/500 , 30 < x < 50
Το ΚΟΘ μπορεί να σου φανεί χρήσιμο στην β . Έστω Xi ο χρόνος του ταξιδιού την i μέρα , με το
i να τρέχει απο 1 εως 50 . Άρα ζητάς το P( E(xi) > 31 ) => P( Σxi/50 > 31) => P( S > 1550 )
Όπου S = Σxi ~ N(nμ, nσ²) , όπου μ & σ τα υπολογίζεις απο την f παραπάνω κτλπ. κτλπ.
Edit : Μετά την παράθεση του Μάρκου , κοίταξα πάλι την άσκηση ,και διαπίστωσα οτι είχα βάλει ανάποδα το 0.55 & 0.45 στην κορυφή
 . Ουσιαστικά η κεντρική ιδέα δεν αλλάζει κάνω τι ίδιο πράγμα και εγώ,απλά στις πιθανότητες με βοηθάει περισσότερο το σχήμα .
. Ουσιαστικά η κεντρική ιδέα δεν αλλάζει κάνω τι ίδιο πράγμα και εγώ,απλά στις πιθανότητες με βοηθάει περισσότερο το σχήμα .Τα 1/10 & 1/25 έχουν προκύψει απο τις δυο κατανομές που μας δίνονται απο την υπόθεση, ενώ οι τελικές τιμές της f βρίσκονται με πολλαπλασιασμούς των πιθανοτήτων των αντίστοιχων κλάδων και διαίρεση του τελικού αποτελέσματος δια το διάστημα της εκάστοτε κατανομής . Στην περίπτωση που 25 < x < 30 πρέπει να ληφθεί ως τελικό αποτέλεσμα το άθροισμα των τιμών που προέκυψαν απο διαδοχικό πολλαπλασιασμών των τιμών απο τον κάθε κλάδο .
Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Μάρκος Βασίλης
Πολύ δραστήριο μέλος


- Πρώτα στρίβεις ένα «άτιμο» νόμισμα που με πιθανότητα 0.55 φέρνει κορώνα (κίνηση) και με πιθανότητα 0,45 γράμματα (όχι κίνηση).
- Μετά, αν έφερες κορώνα ζημιώνεσαι με ένα ποσό Χ τυχαία (δηλ. ομοιόμορφα) επιλεγμένο από το διάστημα [25,50]. Αν όμως έφερες γράμματα, ζημιώνεσαι με ένα ποσό Χ τυχαία επιλεγμένο από το διάστημα [20,30].
Λοιπόν, για τη σ.π.π. το πιο εύκολο που έχεις να κάνεις είναι να βρεις τη συνάρτηση κατανομής πρώτα που έχει και μία απλή διαισθητική ερμηνεία - εκφράζει αθροιστική πιθανότητα. Θα συμβολίζουμε με Χ την τυχαία μεταβλητή που μετράει τη ζημιά μας γενικά (αγνοούμε το πρόσημο αφού είναι πάντα -) ενώ με Υ θα συμβολίζουμε την τυχαία μεταβλητή που μετράει τη ζημιά στην περίπτωση κορώνας και Ζ τη ζημιά μας στην περίπτωση γραμμάτων. Τότε, από το θεώρημα ολικής πιθανότητας έχουμε:
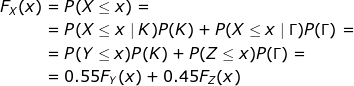
Τώρα, εδώ μπορείς να παραγωγίσεις και να βρεις τη συνάρτηση πυκνότητας. Πρόσεξε μόνο ότι εν γένει δεν παραγωγίζεται η συνάρτηση κατανομής στα tricky σημεία, δηλαδή στο 20, στο 25, στο 30 και στο 50 - εκ των υστέρων μπορεί να βγει παραγωγίσιμη σε κάποια από αυτά αλλά a priori δεν το ξέρουμε.
Οπότε έχουμε:
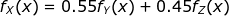
αφού η παράγωγος της κατανομής είναι η πυκνότητα (εκεί που υπάρχει). Τώρα, αν λάβεις υπ' όψιν και ότι
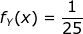
για χ στο [25,50] και μηδέν εκτός αυτού και ότι
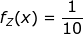
για x στο [20,30] παίρνεις:
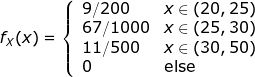
Τώρα, στα άκρα των διαστημάτων όρισέ την όπως θέλεις - δεν έχει σημασία, άλλωστε.
Τώρα, από όλα τα παραπάνω, σημασία έχει η διαίσθηση που κουβαλάει η σχέση:
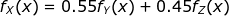
Τι σου λέει πρακτικά (δηλ. μπακάλικα και με μία μικρή αβλεψία) αυτό; Ότι η σχετική πιθανότητα (η σ.π.π. δε μετράει πιθανότητα αλλά σχετική πιθανότητα) να ζημιωθείς με ένα ποσό χ (κίνηση) είναι ένας σταθμισμένος μέσος όρος των πιθανοτήτων να ζημιωθείς με τον τρόπο που ζημιώνεσαι στη μία περίπτωση (Υ), επί την πιθανότητα να εμπίπτεις σε αυτήν την περίπτωση (0.55) συν την πιθανότητα να ζημιωθείς όπως στην άλλη περίπτωση (Ζ) επί την πιθανότητα να εμπίπτεις σε αυτήν την περίπτωση (0.45).
Με άλλα λόγια, είναι σαν να παίρνεις μία «μορφή» του Θεωρήματος Ολικής Πιθανότητας για τις σ.π.π. - παρόλο που δεν εκφράζουν πιθανότητες οι σ.π.π..
Τώρα, η μέση τιμή βγαίνει εύκολα αφού ξέρεις τη σ.π.π..
Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
eukleidhs1821
Διάσημο μέλος


γαμωτο κοντα επεσα την ακουμπησα την λυση αλλα στο τελος τα εκανα μανταρα στο σημειο που συναληθευουν!δηλαδη ενω το επιασα το νοημα με τη σχεση αυτη που εβαλες δεν μου εκοψε στο τελος να παρω ξεχωριστες περιπτωσεις για τα χ που συναληθευουν!!Δηλαδη στον κοινο χρονο 25-30 μπορει να ειναι με κινηση μπορει και οχι.Τεσπα πολυ ωραια η λυση σου.Σκέψου ότι παίζεις το εξής παιχνίδι:
Το ίδιο με άλλα λόγια - εμένα μου αρέσουν τα παιχνίδια περισσότερο, οπότε τα περισσότερα προβλήματα τα έγραφα έτσι. :Ρ
- Πρώτα στρίβεις ένα «άτιμο» νόμισμα που με πιθανότητα 0.55 φέρνει κορώνα (κίνηση) και με πιθανότητα 0,45 γράμματα (όχι κίνηση).
- Μετά, αν έφερες κορώνα ζημιώνεσαι με ένα ποσό Χ τυχαία (δηλ. ομοιόμορφα) επιλεγμένο από το διάστημα [25,50]. Αν όμως έφερες γράμματα, ζημιώνεσαι με ένα ποσό Χ τυχαία επιλεγμένο από το διάστημα [20,30].
Λοιπόν, για τη σ.π.π. το πιο εύκολο που έχεις να κάνεις είναι να βρεις τη συνάρτηση κατανομής πρώτα που έχει και μία απλή διαισθητική ερμηνεία - εκφράζει αθροιστική πιθανότητα. Θα συμβολίζουμε με Χ την τυχαία μεταβλητή που μετράει τη ζημιά μας γενικά (αγνοούμε το πρόσημο αφού είναι πάντα -) ενώ με Υ θα συμβολίζουμε την τυχαία μεταβλητή που μετράει τη ζημιά στην περίπτωση κορώνας και Ζ τη ζημιά μας στην περίπτωση γραμμάτων. Τότε, από το θεώρημα ολικής πιθανότητας έχουμε:
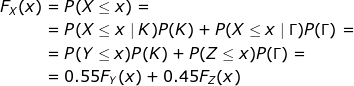
Τώρα, εδώ μπορείς να παραγωγίσεις και να βρεις τη συνάρτηση πυκνότητας. Πρόσεξε μόνο ότι εν γένει δεν παραγωγίζεται η συνάρτηση κατανομής στα tricky σημεία, δηλαδή στο 20, στο 25, στο 30 και στο 50 - εκ των υστέρων μπορεί να βγει παραγωγίσιμη σε κάποια από αυτά αλλά a priori δεν το ξέρουμε.
Οπότε έχουμε:
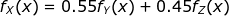
αφού η παράγωγος της κατανομής είναι η πυκνότητα (εκεί που υπάρχει). Τώρα, αν λάβεις υπ' όψιν και ότι
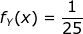
για χ στο [25,50] και μηδέν εκτός αυτού και ότι
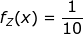
για x στο [20,30] παίρνεις:
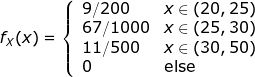
Τώρα, στα άκρα των διαστημάτων όρισέ την όπως θέλεις - δεν έχει σημασία, άλλωστε.
Τώρα, από όλα τα παραπάνω, σημασία έχει η διαίσθηση που κουβαλάει η σχέση:
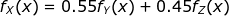
Τι σου λέει πρακτικά (δηλ. μπακάλικα και με μία μικρή αβλεψία) αυτό; Ότι η σχετική πιθανότητα (η σ.π.π. δε μετράει πιθανότητα αλλά σχετική πιθανότητα) να ζημιωθείς με ένα ποσό χ (κίνηση) είναι ένας σταθμισμένος μέσος όρος των πιθανοτήτων να ζημιωθείς με τον τρόπο που ζημιώνεσαι στη μία περίπτωση (Υ), επί την πιθανότητα να εμπίπτεις σε αυτήν την περίπτωση (0.55) συν την πιθανότητα να ζημιωθείς όπως στην άλλη περίπτωση (Ζ) επί την πιθανότητα να εμπίπτεις σε αυτήν την περίπτωση (0.45).
Με άλλα λόγια, είναι σαν να παίρνεις μία «μορφή» του Θεωρήματος Ολικής Πιθανότητας για τις σ.π.π. - παρόλο που δεν εκφράζουν πιθανότητες οι σ.π.π..
Τώρα, η μέση τιμή βγαίνει εύκολα αφού ξέρεις τη σ.π.π..
το οτι δεν ειναι στανταρ παραγωγισιμη στα ακρα πως το ξερεις?
Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Μάρκος Βασίλης
Πολύ δραστήριο μέλος


γαμωτο κοντα επεσα την ακουμπησα την λυση αλλα στο τελος τα εκανα μανταρα στο σημειο που συναληθευουν!δηλαδη ενω το επιασα το νοημα με τη σχεση αυτη που εβαλες δεν μου εκοψε στο τελος να παρω ξεχωριστες περιπτωσεις για τα χ που συναληθευουν!!Δηλαδη στον κοινο χρονο 25-30 μπορει να ειναι με κινηση μπορει και οχι.Τεσπα πολυ ωραια η λυση σου.
Αυτόματη ένωση συνεχόμενων μηνυμάτων:
το οτι δεν ειναι στανταρ παραγωγισιμη στα ακρα πως το ξερεις?
Για την παραγωγισιμότητα, άμα τη σχεδιάσεις φαίνεται. :Ρ Αλλά, πέρα από αυτό, αν η F (η κατανομή) ήταν παραγωγίσιμη τότε θα έπρεπε η παράγωγός της να ικανοποιεί την ιδιότητα της μέσης τιμής, και, επειδή η f (η σ.π.π.) είναι μη σταθερή, θα έπρεπε το σύνολο τιμών της να είναι διάστημα - και άρα (υπεραριθμήσιμα) άπειρο. Ωστόσο το σύνολο τιμών της f είναι πεπερασμένο.
Βασικά, το πιο απλό είναι να τη βάλεις στο geogebra. :Ρ
Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Naki_Marina
Νεοφερμένο μέλος


Ουαου, τώρα βγάζει απόλυτο νόημα! Θα προσπαθώ και εγώ να το μετατρέπω σε παιχνίδι στο μυαλό μου! Ευχαριστώ πααρα πολύ!Σκέψου ότι παίζεις το εξής παιχνίδι:
Το ίδιο με άλλα λόγια - εμένα μου αρέσουν τα παιχνίδια περισσότερο, οπότε τα περισσότερα προβλήματα τα έγραφα έτσι. :Ρ
- Πρώτα στρίβεις ένα «άτιμο» νόμισμα που με πιθανότητα 0.55 φέρνει κορώνα (κίνηση) και με πιθανότητα 0,45 γράμματα (όχι κίνηση).
- Μετά, αν έφερες κορώνα ζημιώνεσαι με ένα ποσό Χ τυχαία (δηλ. ομοιόμορφα) επιλεγμένο από το διάστημα [25,50]. Αν όμως έφερες γράμματα, ζημιώνεσαι με ένα ποσό Χ τυχαία επιλεγμένο από το διάστημα [20,30].
Λοιπόν, για τη σ.π.π. το πιο εύκολο που έχεις να κάνεις είναι να βρεις τη συνάρτηση κατανομής πρώτα που έχει και μία απλή διαισθητική ερμηνεία - εκφράζει αθροιστική πιθανότητα. Θα συμβολίζουμε με Χ την τυχαία μεταβλητή που μετράει τη ζημιά μας γενικά (αγνοούμε το πρόσημο αφού είναι πάντα -) ενώ με Υ θα συμβολίζουμε την τυχαία μεταβλητή που μετράει τη ζημιά στην περίπτωση κορώνας και Ζ τη ζημιά μας στην περίπτωση γραμμάτων. Τότε, από το θεώρημα ολικής πιθανότητας έχουμε:
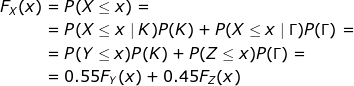
Τώρα, εδώ μπορείς να παραγωγίσεις και να βρεις τη συνάρτηση πυκνότητας. Πρόσεξε μόνο ότι εν γένει δεν παραγωγίζεται η συνάρτηση κατανομής στα tricky σημεία, δηλαδή στο 20, στο 25, στο 30 και στο 50 - εκ των υστέρων μπορεί να βγει παραγωγίσιμη σε κάποια από αυτά αλλά a priori δεν το ξέρουμε.
Οπότε έχουμε:
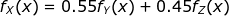
αφού η παράγωγος της κατανομής είναι η πυκνότητα (εκεί που υπάρχει). Τώρα, αν λάβεις υπ' όψιν και ότι
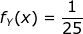
για χ στο [25,50] και μηδέν εκτός αυτού και ότι
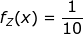
για x στο [20,30] παίρνεις:
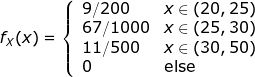
Τώρα, στα άκρα των διαστημάτων όρισέ την όπως θέλεις - δεν έχει σημασία, άλλωστε.
Τώρα, από όλα τα παραπάνω, σημασία έχει η διαίσθηση που κουβαλάει η σχέση:
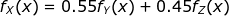
Τι σου λέει πρακτικά (δηλ. μπακάλικα και με μία μικρή αβλεψία) αυτό; Ότι η σχετική πιθανότητα (η σ.π.π. δε μετράει πιθανότητα αλλά σχετική πιθανότητα) να ζημιωθείς με ένα ποσό χ (κίνηση) είναι ένας σταθμισμένος μέσος όρος των πιθανοτήτων να ζημιωθείς με τον τρόπο που ζημιώνεσαι στη μία περίπτωση (Υ), επί την πιθανότητα να εμπίπτεις σε αυτήν την περίπτωση (0.55) συν την πιθανότητα να ζημιωθείς όπως στην άλλη περίπτωση (Ζ) επί την πιθανότητα να εμπίπτεις σε αυτήν την περίπτωση (0.45).
Με άλλα λόγια, είναι σαν να παίρνεις μία «μορφή» του Θεωρήματος Ολικής Πιθανότητας για τις σ.π.π. - παρόλο που δεν εκφράζουν πιθανότητες οι σ.π.π..
Τώρα, η μέση τιμή βγαίνει εύκολα αφού ξέρεις τη σ.π.π..

Χμμ ναι το κατάλαβα! Τώρα είναι η πρώτη μου φορά που μαθαίνω πιθανότητες γιαυτό είχα μπερδευτεί αρκετά! Ευχαριστώ πολύ, και μπορεί να ξαναχρειαστώ τα φώτα όλων εδώ στο κοντινό μέλλον!Για την συνάρτηση πυκνότητας πιθανότητας :
f(x) =
9/200 , 20 < x < 25
67/1000 , 25 < x < 30
11/500 , 30 < x < 50
Το ΚΟΘ μπορεί να σου φανεί χρήσιμο στην β . Έστω Xi ο χρόνος του ταξιδιού την i μέρα , με το
i να τρέχει απο 1 εως 50 . Άρα ζητάς το P( E(xi) > 31 ) => P( Σxi/50 > 31) => P( S > 1550 )
Όπου S = Σxi ~ N(nμ, nσ²) , όπου μ & σ τα υπολογίζεις απο την f παραπάνω κτλπ. κτλπ.
Edit : Μετά την παράθεση του Μάρκου , κοίταξα πάλι την άσκηση ,και διαπίστωσα οτι είχα βάλει ανάποδα το 0.55 & 0.45 στην κορυφή. Ουσιαστικά η κεντρική ιδέα δεν αλλάζει κάνω τι ίδιο πράγμα και εγώ,απλά στις πιθανότητες με βοηθάει περισσότερο το σχήμα .
Τα 1/10 & 1/25 έχουν προκύψει απο τις δυο κατανομές που μας δίνονται απο την υπόθεση, ενώ οι τελικές τιμές της f βρίσκονται με πολλαπλασιασμούς των πιθανοτήτων των αντίστοιχων κλάδων και διαίρεση του τελικού αποτελέσματος δια το διάστημα της εκάστοτε κατανομής . Στην περίπτωση που 25 < x < 30 πρέπει να ληφθεί ως τελικό αποτέλεσμα το άθροισμα των τιμών που προέκυψαν απο διαδοχικό πολλαπλασιασμών των τιμών απο τον κάθε κλάδο .
View attachment 69823

Επίσης, για να σιγουρευτώ, στον υπολογισμό των σ και μ, χρησιμοποιώ σαν άκρα (α και β) όλο το διάστημα που ισχύει η f, δηλαδή το [20,50], ή το διάστημα που [30,50], το οποίο είναι το διάστημα που ζητάει?
Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Μάρκος Βασίλης
Πολύ δραστήριο μέλος


Ουαου, τώρα βγάζει απόλυτο νόημα! Θα προσπαθώ και εγώ να το μετατρέπω σε παιχνίδι στο μυαλό μου! Ευχαριστώ πααρα πολύ!
Αυτόματη ένωση συνεχόμενων μηνυμάτων:
Χμμ ναι το κατάλαβα! Τώρα είναι η πρώτη μου φορά που μαθαίνω πιθανότητες γιαυτό είχα μπερδευτεί αρκετά! Ευχαριστώ πολύ, και μπορεί να ξαναχρειαστώ τα φώτα όλων εδώ στο κοντινό μέλλον!
Επίσης, για να σιγουρευτώ, στον υπολογισμό των σ και μ, χρησιμοποιώ σαν άκρα (α και β) όλο το διάστημα που ισχύει η f, δηλαδή το [20,50], ή το διάστημα που [30,50], το οποίο είναι το διάστημα που ζητάει?
Για το σ και το μ πας με τη συνάρτηση πιθανότητας f που βρήκες παραπάνω για την τ.μ. Χ. Και μετά κάνεις ένα κεντρικό οριακό θεώρημα κ.λπ.
Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Samael
Τιμώμενο Μέλος


Ουαου, τώρα βγάζει απόλυτο νόημα! Θα προσπαθώ και εγώ να το μετατρέπω σε παιχνίδι στο μυαλό μου! Ευχαριστώ πααρα πολύ!
Αυτόματη ένωση συνεχόμενων μηνυμάτων:
Χμμ ναι το κατάλαβα! Τώρα είναι η πρώτη μου φορά που μαθαίνω πιθανότητες γιαυτό είχα μπερδευτεί αρκετά! Ευχαριστώ πολύ, και μπορεί να ξαναχρειαστώ τα φώτα όλων εδώ στο κοντινό μέλλον!
Επίσης, για να σιγουρευτώ, στον υπολογισμό των σ και μ, χρησιμοποιώ σαν άκρα (α και β) όλο το διάστημα που ισχύει η f, δηλαδή το [20,50], ή το διάστημα που [30,50], το οποίο είναι το διάστημα που ζητάει?
Κανένα πρόβλημα
 .
.Για τον υπολογισμό των σ & μ όπως είπε και ο Μάρκος χρησιμοποιείς την f . Επειδή προέκυψε με ένα-δυο παραπάνω κόλπα στον τρόπο σκέψης δεν αλλάζει η ουσία του αποτελέσματος . Mια σ.π.π είναι όπως όλες οι άλλες, ορισμένη σε ένα διάστημα . Απο 20 εως 50 . Άρα σε αυτό θα υπολογίσεις(προφανώς σπαστά γιατί αλλάζει ο τύπος ενδιάμεσα) τα μ & σ .
Σε ποιο ερώτημα ζήταγε να κάνεις κάτι συγκεκριμένα στο διάστημα [20,50] ή [30,50] ;
Ξέχνα τις αρχικές κατανομές,δεν παίζουν κανένα ρόλο πλέον,πήρες οτι πληροφορία χρειαζόσουν απο αυτές .
Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 0 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 27 μέλη διάβασαν αυτό το θέμα:
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki

