ultraviolence
Τιμώμενο Μέλος


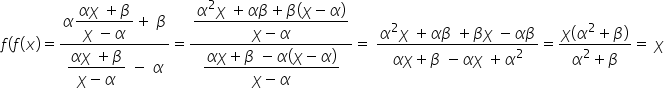
Στο β όταν κάνεις
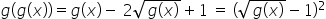
Ελπίζω να βοήθησα!
edit: Για να είναι ολόσωστο, πρέπει να βρεις και το πεδίο ορισμού της fof/gog.
Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Scandal
Διαχειριστής



Δεν το είδα καλά!
Εύκολη ασκησούλα, ευχαριστώ!! Ναι το ξέρω ότι πρέπει να βρίσκω και τα Df/ Dg.

Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
ougka pougka
Εκκολαπτόμενο μέλος



Υγ. Μην πει κανενας ολοκληρωμα τον εφαγα
Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Giorgos496
Νεοφερμένος


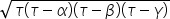
Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Samael
Τιμώμενο Μέλος


Εχω να υπολογισω επειγοντως ενα εμβαδο οξυγωνιου τριγωνου, αλλα δε γνωριζω ουτε τις γωνιες ουτε το υψος του. Μονο τα μηκη των πλευρων του. Καμια ιδεα?
Υγ. Μην πει κανενας ολοκληρωμα τον εφαγα
Εναλλακτικα μπορεις να υπολογισεις το εμβαδον και απο τον τυπο :
Eτριγ = |det(ΑΒ,ΑΓ)|/2
Οπου ΑΒ = (XΒ-ΧΑ , ΥΒ-ΥΑ) , ΑΓ = (ΧΓ-XΑ,ΥΓ-YA).
det(ΑΒ,ΑΓ) =
|XΒ-ΧΑ ΧΓ-XΑ| = (XΒ-ΧΑ)(ΥΓ-ΥΑ)-(ΧΓ-ΧΑ)(ΥΒ-ΥΑ)
|ΥΒ-ΥΑ ΥΓ-YA|
Δηλαδη Ετργ = |(XΒ-ΧΑ)(ΥΓ-ΥΑ)-(ΧΓ-ΧΑ)(ΥΒ-ΥΑ)|/2
Οπου ΧΒ-ΧΑ τετμημενη περατος του διανυσματος που ειναι παραλληλο στην ευθεια που ενωνει τα σημεια Α,Β και εχει μετρο ισο με το ευθυγραμμο τμημα ΑΒ. Αντιστοιχα για YΓ-YΑ που ειναι η τεταγμενη του περατος .
Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
ougka pougka
Εκκολαπτόμενο μέλος



Σαμαελ δεν εχω συντεταγμενες δυστυχως, μονο τα μηκη...
Νομιζω οτι βγαινει και με το νομο των συνημιτονων, τωρα που το σκεφτομαι. Αλλα ο τυπος του Ηρωνα σε γλιτωνει απο πολλες πραξεις
Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Samael
Τιμώμενο Μέλος


Ποιος θα το φανταζοταν οτι ο τυπος του Ηρωνα θα μου χρησιμευε καποτε...τι ηρωνεια
Σαμαελ δεν εχω συντεταγμενες δυστυχως, μονο τα μηκη...
Νομιζω οτι βγαινει και με το νομο των συνημιτονων, τωρα που το σκεφτομαι. Αλλα ο τυπος του Ηρωνα σε γλιτωνει απο πολλες πραξεις
Πραγματι εχεις δικιο,ειχα κανει και λαθος στην οριζουσα τωρα το ειδα και το διορθωσα
 .Προσεξε ομως οτι στον τελικο τυπο σε ενδιαφερουν οι διαφορες των συντεταγμενων,δηλαδη μηκη. Αρα εαν εχεις κλιμακα μπορεις να μετρησεις με τον χαρακα και να ματετρεψεις,δεν χρειαζεται δηλαδη να ξερεις συντεταγμενες
.Προσεξε ομως οτι στον τελικο τυπο σε ενδιαφερουν οι διαφορες των συντεταγμενων,δηλαδη μηκη. Αρα εαν εχεις κλιμακα μπορεις να μετρησεις με τον χαρακα και να ματετρεψεις,δεν χρειαζεται δηλαδη να ξερεις συντεταγμενες  .
.Παντως εαν δεν θυμασαι και απολυτως τιποτα μπορεις να χρησιμοποιησεις και το πυθαγορειο.Ειπες οτι ξερεις μηκη πλευρων οποτε ξερεις το μηκος της βασης και σου μενει να βρεις το υψος.Φερνεις λοιπον το υψος και σχηματιζονται 2 ορθογωνια τριγωνα τα οποια εχουν κοινη πλευρα το υψος εστω y και βασεις x και x-Α αντοιστοιχα οπου Α το μηκος της βασης. Εχεις δυο εξισωσεις και δυο αγνωστους(το υψος y και την μια βαση x). Απο το πυθαγορειο σχηματιζεις δυο εξισωσεις και απο εκει βρισκεις την βαση και το υψος οποτε υπολογιζεις απο τον τυπο E = (1/2)yx + (1/2)y(A-x).
Τα παραπανω τα λεω απλα για να υπαρχει ποικιλλια λυσεων στο προβλημα γιατι φετος υπηρχε μεγαλη απορια για το εμβαδον κυκλου οποτε σε γεωμετρικα προβληματα ειναι σημαντικο να παρουσιαζουμε αρκετες λυσεις.Γενικα δηλαδη εαν δεν θυμαται κανεις κατι ειναι καλο να αυτοσχεδιαζει.Στα μαθηματικα παντα υπαρχει τροπος να φτασεις στο ζητουμενο αρκει να θυμασαι κατι βασικο εστω και στοιχειωδες και απο εκει να δουλεψεις. Ο πιο ευκολος τροπος ειναι προφανεστατα ο τυπος του Ηρων.Θεωρω οτι οι παραπανω μεθοδοι ωστοσο ειναι χρησιμοι διοι θα ενισχυσουν την ευελιξια καποιου ή εαν δεν θελει να θυμαται τυπους η ξεχναει ευκολα
 .
.Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


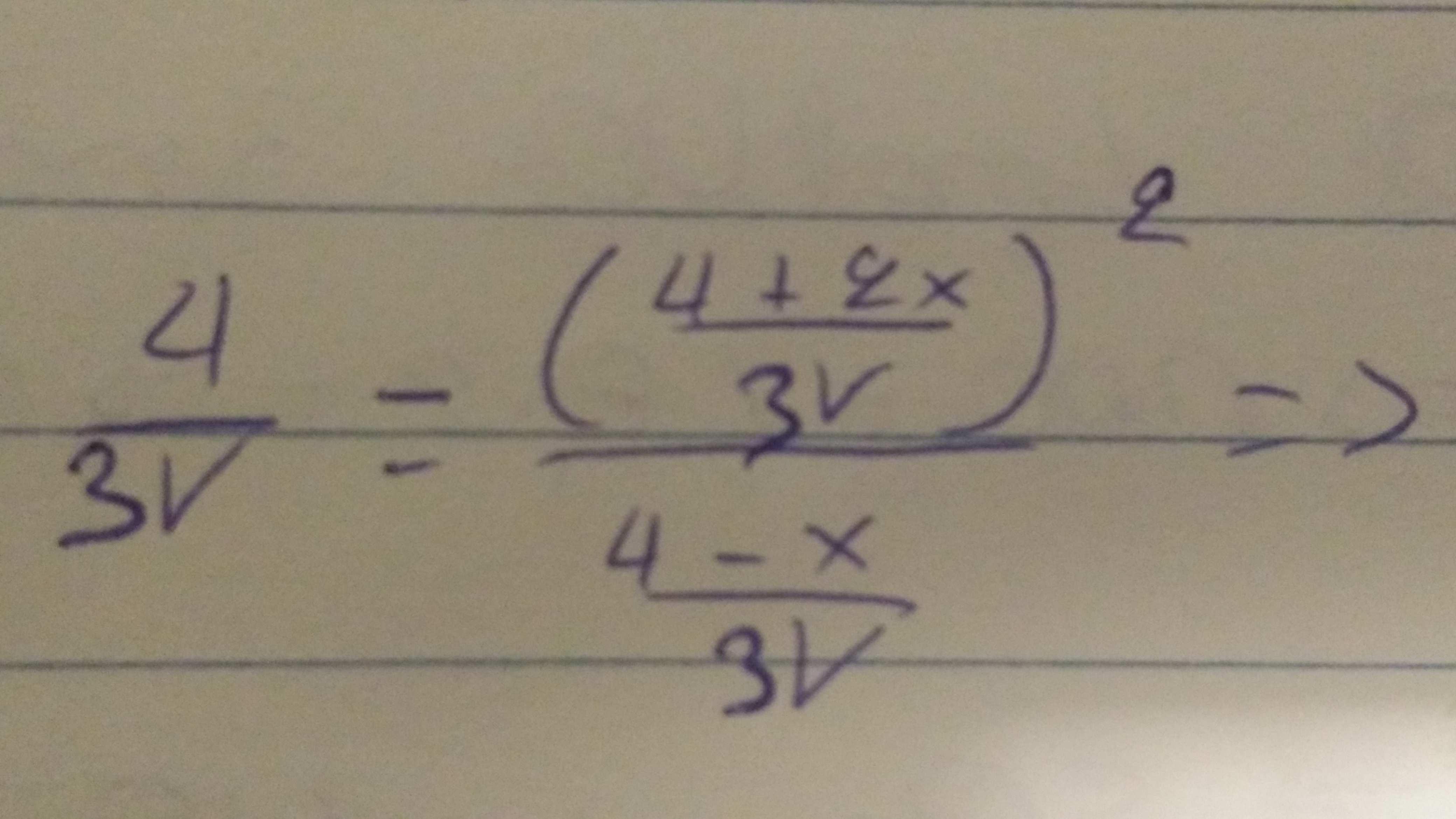
Έχω κολλήσει κι δεν μπορώ να το λύσω πως να το συνεχίσω;
Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Indiana Jones
Δραστήριο μέλος


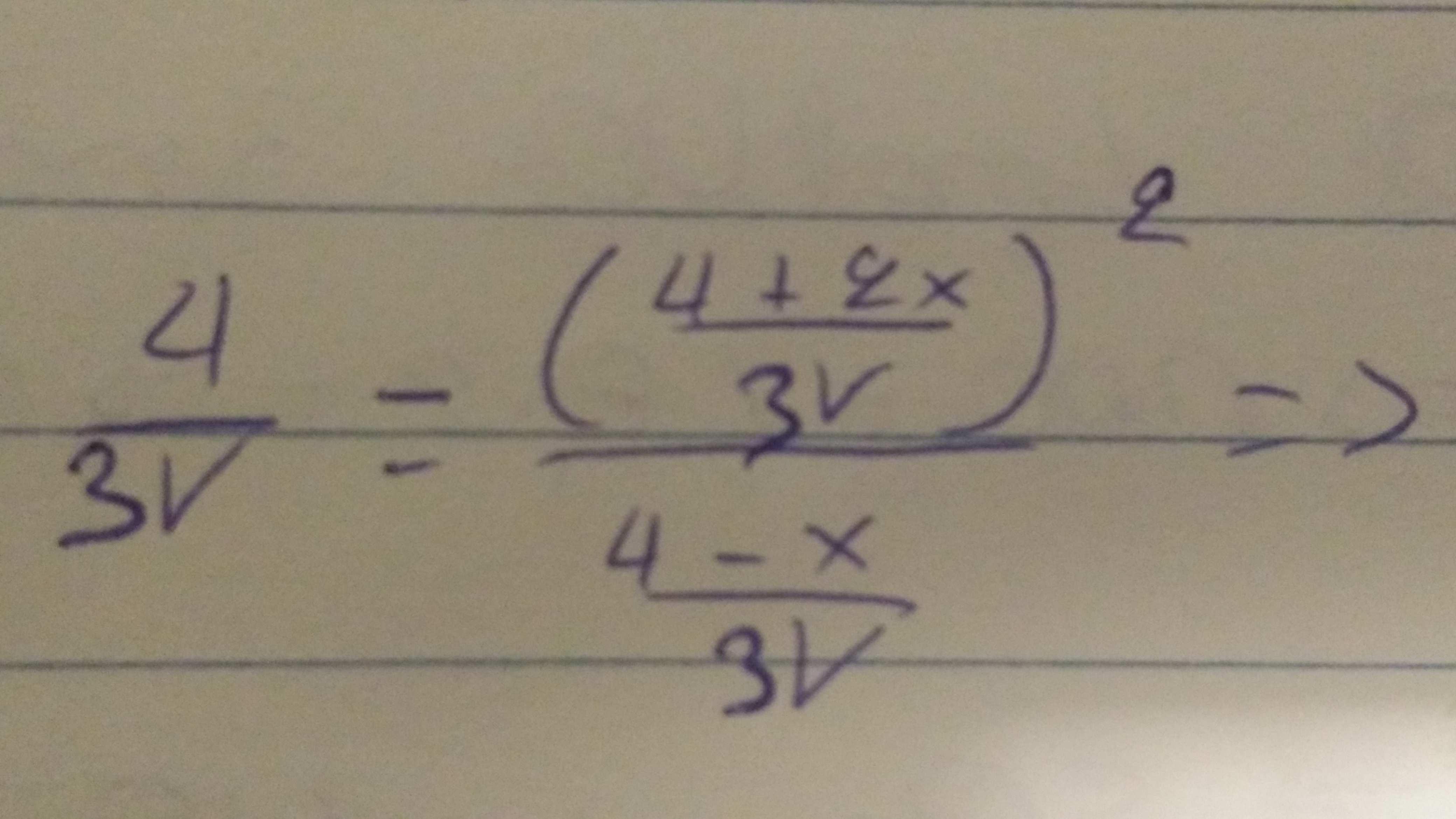
Έχω κολλήσει κι δεν μπορώ να το λύσω πως να το συνεχίσω;
Στο δεύτερο μέλος θα βάλεις το τετράγωνο μέσα κάνοντας πράξεις,άκρους-μέσους μετά,χιαστί και λύνεις ως προς ν.
Τουλάχιστον αυτό μου είπε ο αδερφός μου που είναι θετική και το κατάλαβα. Εγώ είμαι θεωρητική,μη σε πάρω και στο λαιμό μου.

Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Samael
Τιμώμενο Μέλος


Στο δεύτερο μέλος θα βάλεις το τετράγωνο μέσα κάνοντας πράξεις,άκρους-μέσους μετά,χιαστί και λύνεις ως προς ν.
Τουλάχιστον αυτό μου είπε ο αδερφός μου που είναι θετική και το κατάλαβα. Εγώ είμαι θεωρητική,μη σε πάρω και στο λαιμό μου.
Τα V φευγουν εαν το δεις μερικα βηματα πιο μπροστα,επειδη απλοποιουνται και λυνει το πολυωνυμο δευτερου βαθμου που προκυπτει . Αλλα για θεωρητικη ωραιος
 .
.Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Jim_Pap
Εκκολαπτόμενο μέλος


Γραψτο 4/3V=[(4-x)(4+2x)^2]/3V και αρα λυνεις την (4-χ)(4+2χ)^2=4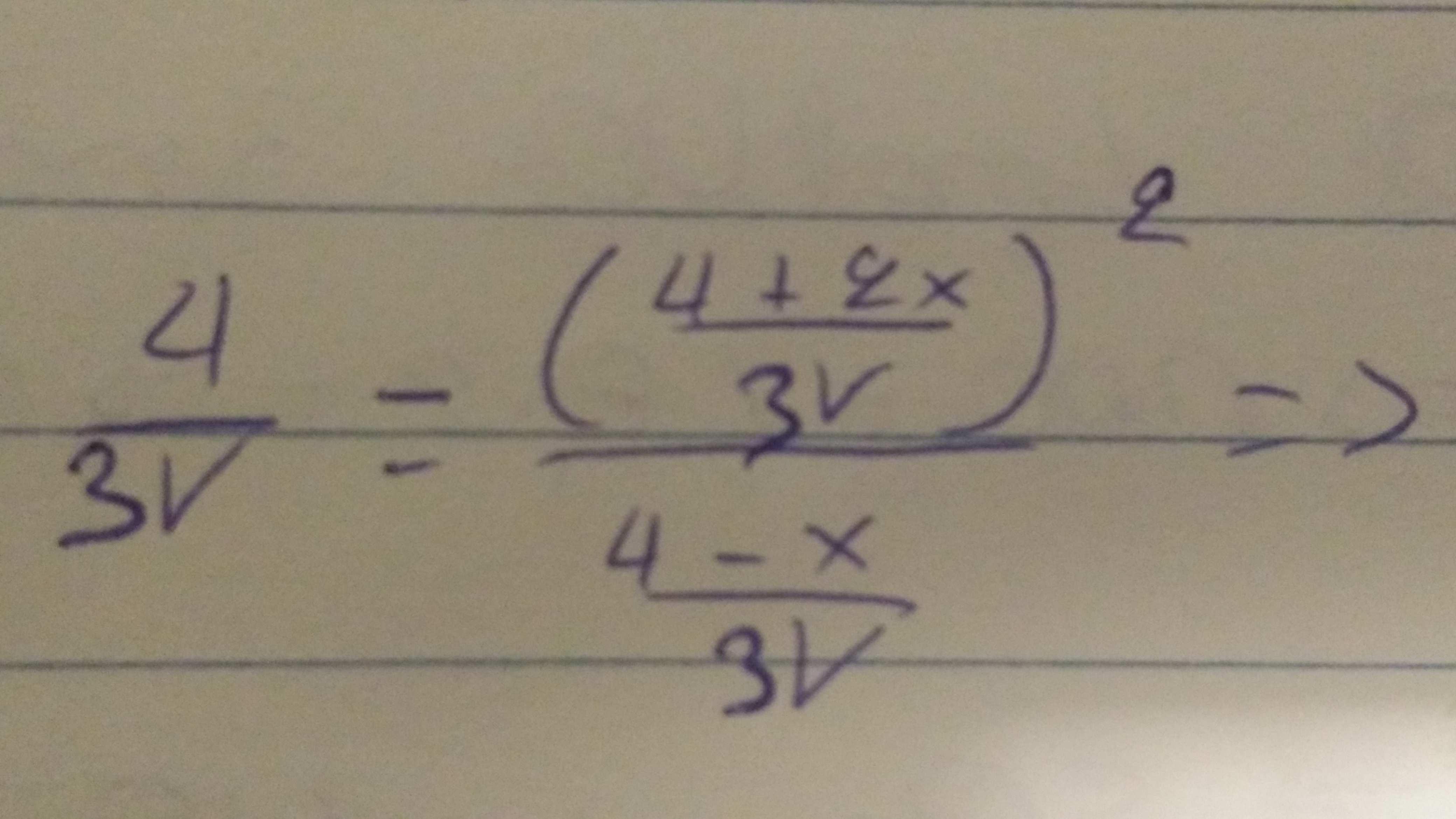
Έχω κολλήσει κι δεν μπορώ να το λύσω πως να το συνεχίσω;
Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Αγγελος Κοκ
Τιμώμενο Μέλος


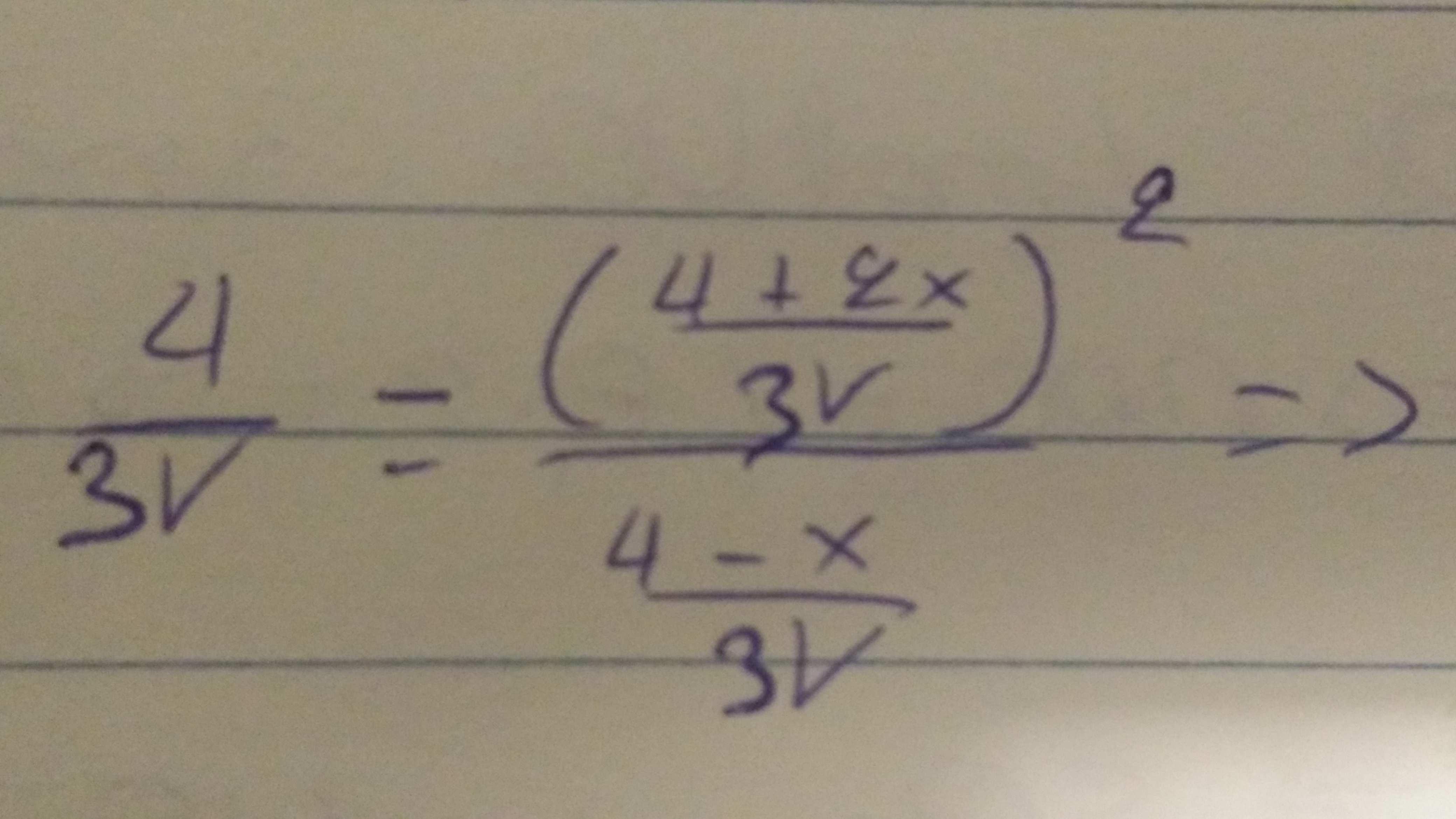
Έχω κολλήσει κι δεν μπορώ να το λύσω πως να το συνεχίσω;
Στο β μελος το 3v πηγαινει πανω.Αρα διαιρεις με 3v,κανεις χιαστη και εχεις:
4(4-x)/(3v)^2=(4+2x)^2/(3v)^2<=>16-4x=16+16x+4x^2<=>4x^2+20x=0<=>4x(x+5)=0<=>x=0 ή x=5,δεδομενου ότι v διαφορο του μηδενος
Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Samael
Τιμώμενο Μέλος


Καλησπέρα παιδιά.Μήπως γνωρίζει κάποιος να μου πει ποια είναι η απόδειξη του de l'hopital;;;
Στο πλαισιο της Γ λυκειου η αποδειξη του θεωρηματος του L'Hôpital δεν ζητειται.
Εαν ωστοσο σε ενδιαφερει γενικα να την δεις θα πρεπει να ψαξεις καποιο βιβλιο η βιντεο που κανει εισαγωγη στην πραγματικη αναλυση που σαφως συζητιουνται οι εννοιες του λογισμου αλλα με πολυ μεγαλυτερη αυστηροτητα στον ορισμο και εμφαση στις αποδειξεις.
 .
.Μπορω να κανω μια αποπειρα να σου δειξω γιατι ισχυει ομως στην περιπτωση του 0 προς 0 οριου,χωρις αυτη την αυστηροτητα,για να το καταλαβεις πιο πολυ διαισθητικα :
Εστω lim x->xo[f(x)/g(x)] = λ
Εστω οτι f(xo)=g(xo)=0 και f,g παραγωγισιμες στο πεδιο ορισμου τους.
Τοτε κοντα στο xo εχουμε :
lim x->xo[(f(x)-f(xo))/(x-xo)] = lim x->xo[f(x)/(x-xo)] = f'(xo)
Ομοιως lim x->xo[(g(x)-g(xo))/x-xo)] = lim x->xo[g(x)/(x-xo)] = g'(xo)
Απο τα παραπανω εχουμε :
λ = lim x->xo[f(x)/g(x)] = lim x->xo[(f(x)/x-xo)/(g(x)/x-xo] = f'(xo)/g'(xo)
Προσοχη ο κανονας λεει οτι εαν υπαρχει το κλασμα f'(xo)/g'(xo) τοτε η λυση του ειναι η ιδια και για το αρχικο οριο.Αλλα εαν δεν υπαρχει αυτο δεν σημαινει οτι και το αρχικο οριο δεν υπαρχει επισης.
Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Scandal
Διαχειριστής



Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Αλεξακις
Νεοφερμένος


Ευχαριστώ .

Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Guest 092312
Επισκέπτης


Άρα, στο [0,+00) είναι γνησίως φθίνουσα (0<4 και f(0)=4>f(4)=0) και αντίστοιχα στο (-οο,0) είναι γνησίως αύξουσα με lim_(x->-oo)=-oo
Συνεπώς παρουσιάζει μέγιστο στο 0 το 4, άρα f(Df)=(-oo,4]
2) Για να ορίζεται η f(f(x)) στο R πρέπει να έχει πεδίο ορισμού το R. Dfof=[x ανήκει Df| f(x) ανήκει Df]=...=R
Για τη μονοτονία χώρισε το [-4,4] σε 2 ίσα διαστήματα και κατασκεύασε (αφού ξέρεις τη μονοτονία της f, παίζεις "φορώντας" f)
3)f συνεχής στο R(άρα και στο 4) άρα lim_(x->4)=f(4)=0=lim_(x->4-) (1)f(x)>0 "κοντά" στο 4 από αριστερά (γν. φθίνουσα) (2)
(1),(2)=> lim_(x->4-) (1/(fx))=+oo
4) 1)Ξέρεις ότι f(0)=4 και f(4)=0Με απλές πράξεις g(0)+g(1)+g(2)+g(3)=f(1)-f(0)+1+f(2)-f(1)+1+f(3)-f(2)+1+f(4)-f(3)+1=-f(0)+f(4)+4=-4+0+4=0
2)f(μ+1)=f(μ)-1 <=> f(μ+1)-f(μ)+1=0 <=> g(μ)=0g συνεχής στο [0,3] (ως πράξεις συνεχών, f(x+1) συνεχής ως σύνθεση συνεχών...)g(0)g(3)<0...Bolzano…
Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Αλεξακις
Νεοφερμένος


1)Έχεις τα εξής στοιχεία: η f:R->R είναι άρτια (άρα f(-x)=f(x) για κάθε x εν R, δηλαδή συμμετρική ως προς τον άξονα yy'), συνεχής και γνησίως μονότονη στο [0,+oo). Λόγω συμμετρίας προκύπτει πως είναι γνησίως μονότονη και στο (-oo,0) (και μάλιστα αντίθετης μονοτονίας)
Άρα, στο [0,+00) είναι γνησίως φθίνουσα (0<4 και f(0)=4>f(4)=0) και αντίστοιχα στο (-οο,0) είναι γνησίως αύξουσα με lim_(x->-oo)=-oo
Συνεπώς παρουσιάζει μέγιστο στο 0 το 4, άρα f(Df)=(-oo,4]
2) Για να ορίζεται η f(f(x)) στο R πρέπει να έχει πεδίο ορισμού το R. Dfof=[x ανήκει Df| f(x) ανήκει Df]=...=R
Για τη μονοτονία χώρισε το [-4,4] σε 2 ίσα διαστήματα και κατασκεύασε (αφού ξέρεις τη μονοτονία της f, παίζεις "φορώντας" f)
3)f συνεχής στο R(άρα και στο 4) άρα lim_(x->4)=f(4)=0=lim_(x->4-) (1)f(x)>0 "κοντά" στο 4 από αριστερά (γν. φθίνουσα) (2)
(1),(2)=> lim_(x->4-) (1/(fx))=+oo
4) 1)Ξέρεις ότι f(0)=4 και f(4)=0Με απλές πράξεις g(0)+g(1)+g(2)+g(3)=f(1)-f(0)+1+f(2)-f(1)+1+f(3)-f(2)+1+f(4)-f(3)+1=-f(0)+f(4)+4=-4+0+4=0
2)f(μ+1)=f(μ)-1 <=> f(μ+1)-f(μ)+1=0 <=> g(μ)=0g συνεχής στο [0,3] (ως πράξεις συνεχών, f(x+1) συνεχής ως σύνθεση συνεχών...)g(0)g(3)<0...Bolzano…
Σε ευχαριστώ για την γρήγορη ανταπόκριση .
Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Guest 092312
Επισκέπτης


Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 1 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 270 μέλη διάβασαν αυτό το θέμα:
- Mariosm.
- thepigod762
- soulatso
- oteletampis
- phleidhs
- *
- Μαθητής του 15
- BlackPenBluePen
- AggelikiGr
- *
- sir ImPeCaBlE
- veiNqh
- Scandal
- alekos
- Debugging_Demon
- just some guy
- xristosgkm
- ismember
- Apocalypse
- arrow25
- *
- rempelos42
- *
- ggl
- *
- *
- GStef
- QWERTY23
- xrisamikol
- Σωτηρία
- nikoletaz57
- _Aggelos123
- Mariam38
- *
- SlimShady
- *
- strsismos88
- *
- Georgekk
- Lia 2006
- igeorgeoikonomo
- marian
- tsiobieman
- constansn
- Xristosdimitra
- Panagiotis849
- *
- ρενακι 13
- *
- Memetchi
- eukleidhs1821
- Nikkkpat
- Unboxholics
- korlef
- *
- kwstaseL
- Thanos_D
- *
- the purge
- T C
- Giii
- Papachrist
- liaiscool
- Αννα Τσιτα
- globglogabgalab
- Pharmacist01
- thanahss
- abcdefg12345
- nicole1982
- *
- *
- thecrazycretan
- kvstas92
- KingOfPop
- *
- nPb
- maria301
- papa2g
- stefan
- *
- Κλημεντίνη
- TonyMontanaEse
- Athens2002
- Alexecon1991
- Μάρκος Βασίλης
- *
- Cortes
- το κοριτσι του μαη
- calliope
- *
- *
- *
- *
- ale
- panagiotis G
- *
- Kleanth
- aggelosst9
- BioChemical
- spring day
- nucomer
- Georgia110
- LeoDel
- pink_panther
- Alexandros973
- marsenis
- den antexw allh apotyxia
- KaterinaL
- kiyoshi
- drosos
- Λαμπρινηη
- Bill22
- Chrysablac.
- giorgosp97
- *
- Βλα
- Monster Hunter
- jul25
- xxxtolis
- Stroka
- *
- nicks1999
- totiloz
- *
- Earendil
- mitsakos
- tasost
- lnesb
- ssalex
- Vasilina93
- alan09
- *
- Livaja10
- χημεια4λαιφ
- *
- *
- Viedo
- UncleJ
- Kostakis45
- Infrared
- Zgian
- pepatogourounaki
- hirasawayui
- GeoCommand
- Eleni54
- Volkswagen Fan
- EiriniS20
- Johny4Life
- ΘανάσοςG4
- *
- stamoul1s
- Αριάνα123
- uni77
- Libertus
- tasoss
- *
- PanosCh002
- Unseen skygge
- *
- Νικόλας Ραπ.
- *
- cel123
- The Limit Does Not Exist
- *
- don_vito
- suaimhneas
- Αλκης Κ.
- alexrami
- Baggelitsa36
- Νομικάριος13
- spinalgr1990
- d_th
- *
- Adolfo valencia
- Πα.Κ
- Vasilis25
- Johnman97
- Steffie88
- rekcoR
- *
- gwgw_5
- fockos
- Mariahj
- roud
- kostas83
- Cpt.Philips
- *
- Makis45
- *
- Χρησλου
- Panos_02
- Vold
- *
- *
- tymvorixos
- GiorgosAsi
- Neos167
- *
- *
- theodoraooo
- *
- George187
- Άρτεμις Α.
- Μαρία2222
- christos87
- Idontknoww
- jimis2001
- Metamorph
- Γατόπαρδος.
- Johnsk
- mitsos14
- johnsiak
- *
- Elel
- Dreamer_SW
- Γιαννης1987Θεσσ
- *
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Chat
Chat
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki

