Άσκηση στην ευθεία

[Cade]

Καλησπέρα, μπορεί να με βοηθήσει κάποιος στην επίλυση της παρακάτω άσκησης ; Θα ήθελα μόνο το Α.
Ευχαριστώ

 

[γιαννης_00]

Εχω βρει μια λυση με βαση τα εσωτερικα γινομενα την οποια θεωρω μακροσκελη ηλίθια και αναρμοστη για μια καλη ασκηση. Αν δεν βρεις κατι εξυπνοτερο να στην γραψω.

 

[Cade]

Εχω βρει μια λυση με βαση τα εσωτερικα γινομενα την οποια θεωρω μακροσκελη ηλίθια και αναρμοστη για μια καλη ασκηση. Αν δεν βρεις κατι εξυπνοτερο να στην γραψω.

Ναι μπορείς να την γράψεις. Προσπαθησα να συνδέσω τα λ1, λ2 με το α αλλά δεν μου εβγαινε αποτέλεσμα.

 

[γιαννης_00]

Ναι μπορείς να την γράψεις. Προσπαθησα να συνδέσω τα λ1, λ2 με το α αλλά δεν μου εβγαινε αποτέλεσμα.

Ωραια σχεδιαζω και γραφω, θα παρει λιγο χρνο.

 

[γιαννης_00]

Τελικα δεν ειναι τοσο ασχημη, εχει τοσες πραξεις ωστε να κανεις λαθος ή να καθυστερησεις.
Καλα εκει στο σχεδιο τα λ1 και λ2 δεν ειναι η γωνια αλλα η εφαπτομενη της γωνιας που δειχνουν.

 

[Samael]

Δοκίμασε την εξής λογική εαν θέλεις :

Έστω οι ευθείες ε1 και ε2 με συντελεστές λ1 και λ2 που τέμνονται απο την ευθεία y=α ,στο σημείο Α=(χ1,α) και Β=(χ2,α), αντίστοιχα.

Έστω τώρα ε1' η κάθετη στην ε1,που διέρχεται απο το Α, και ε2' η κάθετη στην ε2,που διέρχεται απο το Β . Η κάθετη στην ε1 θα έχει σ.δ. λ1' = -1/λ1 και η ε2 θα έχει σ.δ. λ2' = -1/λ2.

Άρα καταλήγουμε με εξισώσεις ευθειών :
ε1' : y = -(1/λ1)x+β (1)
ε2' : y = -(1/λ2)χ+γ (2)

Εφόσον οι ευθείες διέρχεται απο τα Α και Β,οι συντεταγμένες τους πρέπει να επαληθεύουν τις εξισώσεις των ευθειών. Έτσι για x = x1 στην (1) και x=x2 στην (2) θα έχουμε :

α = -(1/λ1)x1 + β
α = -(1/λ2)x2 + γ

Όμως x1 = α/λ1,απο την ε1 , και x2 = α/λ2 απο την ε2 . Τελικά οι παραπάνω γράφονται :

α = -(1/λ1)(α/λ1) + β
α = -(1/λ2)(α/λ2) + γ
=>
β = α + α/λ1²
γ = α + α/λ2²
=>
β = α(λ1²+1)/λ1²
γ = α(λ2²+1)/λ2²

Τελικά :
ε1' : y = -(1/λ1)x + α(λ1²+1)/λ1²
ε2' : y = -(1/λ2)x + α(λ2²+1)/λ2²

Για να βρούμε τις συντεταγμένες του σημείο Γ στο οποίο τέμνονται οι δυο κάθετες, λύνουμε το παραπάνω σύστημα που δημιουργούν οι παραπάνω δυο εξισώσεις :

-(1/λ1)x + α(λ1²+1)/λ1² = -(1/λ2)x + α(λ2²+1)/λ2² => *λ1²λ2²
-λ1λ2²x + αλ2²(λ1²+1) = -λ2λ1²x +αλ1²(λ2²+1) =>
(λ2λ1²-λ1λ2²)x = αλ1²(λ2²+1) - αλ2²(λ1²+1) =>

χ->χΓ
χΓ = [αλ1²(λ2²+1) - αλ2²(λ1²+1)] /λ1λ2(λ1-λ2) =>
χΓ = [αλ1²λ2²+αλ1² -αλ1²λ2²-αλ2²]/λ1λ2(λ1-λ2) =>
χΓ = α(λ1-λ2)(λ1+λ2)/λ1λ2(λ1-λ2) =>

Τελικά :
χΓ = α(λ1+λ2)/λ1λ2

Αντικαθιστώντας σε μια απο τις δυο το x που βρήκες, μπορείς να πάρεις και το yΓ . Εαν κάνεις τις πράξεις θα βγάλεις :

yΓ = α(1 - 1/λ1λ2 )

 

[Cade]

Ευχαριστώ πολύ, θα τις κοιτάξω και τις δυο.

 

[γιαννης_00]

Νικο αν ασχοληθηκες θα ειδες το λαθος στην αναπτυξη της παρακατω ταυτοτητας λογω κοπυ παστε.

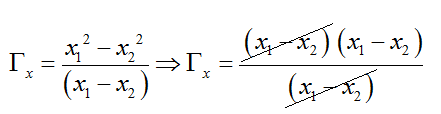
Οποτε εσυ δρας αναλογα, το τυπογραφικο λαθος αυτο επιφερει αλλαγη προσιμων και στις δυο συντεταγμενες.

 

[Cade]

Ναι δεν υπάρχει θέμα, εξάλλου πιο πολύ ήθελα την μεθοδολογία. Ευχαριστώ