Ασκήσεις Μαθηματικών

[Astrix]

Καλησπέρα σας θέλω να βρω μια παραγωγό
του F(x)=3ημ2x f'(x) = ;;;

Σημείωση: Το μήνυμα αυτό γράφτηκε 6 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

 

[Guest 039548]

Ξαναδιαβασε τους βασικους τυπους.
Για απλά παραδειγματα υπαρχουν και υπολογιστες online.

Σημείωση: Το μήνυμα αυτό γράφτηκε 6 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

 

[Samael]

Καλησπέρα σας θέλω να βρω μια παραγωγό
του F(x)=3ημ2x f'(x) = ;;;

Λύσε πολλές τέτοιες ασκήσεις για να μάθεις σωστά τους κανόνες . Που θα έπρεπε να ήσουν κανονικά στην ύλη γιατί έχω την αίσθηση οτι θα έπρεπε να είχατε ήδη κάνει παραγώγους .

f'(x) = (3ημ2x)'

1)Οι σταθερές μπορούν να βγούν εκτός παραγώγου.

f'(x) = 3(ημ2x)'

2) Η συνάρτηση εντός της παραγώγου( h(u) = ημu ) είναι μια σύνθετη συνάρτηση καθώς δεν είναι μια απο τις βασικές συναρτήσεις που ξέρουμε αφού u = 2x .

Άρα σύμφωνα με τον κανόνα της αλυσίδας dh/dx = (dh/du)*(du/dx) . Στην περίπτωση μας :

dh/du = (ημu)' = συνu
du/dx = (2x)' = 2

Άρα (ημ2x)' = 2συν(2x)

Τελικά f'(x) = 3*2*συν(2x) = 6συν(2x) .

Κανόνα πηλίκου,κανόνα γινομένου,κανόνα αλυσίδας,κανόνα σταθεράς,κανόνα πρόσθεσης παραγώγων και παραγώγιση πολυωνύμων,ριζών,λογαρίθμου,τριγωνομετρικών και εκθετικών με βάση το e ή άλλο νούμερο πρέπει να γνωρίζεις οπωσδήποτε ώστε να μπορείς να λύνεις τις ασκήσεις .

Πιθανότατα επίσης να χρησιμοποιείς τον συμβολισμό με τον τόνο ωστόσο εδώ ο συμβολισμός f'(x) και df/dx είναι εντελώς ισοδύναμοι . Προς το παρών δεν φαίνεται να κάνει μεγάλη διαφορά, αλλά επειδή είχα πολλές μεταβλητές , ο τόνος δεν δείχνει κάθε φορά ως προς τι παραγωγίζω . Αργότερα εαν με το καλό περάσεις σε τμήμα που έχεις μπόλικα μαθηματικά θα δεις οτι είναι σημαντική λεπτομέρεια,και καλό θα ήταν να συνηθίζεις απο τώρα τον συμβολισμό . Θεωρώ οτι είναι τόσο εκπαιδευτικά όσο και θεωρητικά πιο καλή ορολογία .

Σημείωση: Το μήνυμα αυτό γράφτηκε 6 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

 

[Astrix]

Ευχαριστώ πολύ Samael..

Σημείωση: Το μήνυμα αυτό γράφτηκε 6 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

 

[Astrix]

καλησπερα σας παιδια... θελω να βρω μια παραγωγο

g(x)= f(2x+1)-2e^2x+1

g'(x) = ;;

g(0) = 0 επειδη η ασκηση λεει f(1) = 2e

Σημείωση: Το μήνυμα αυτό γράφτηκε 6 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

 

[Scandal]

Ο @Samael ίσως μπορεί να βοηθήσει

Σημείωση: Το μήνυμα αυτό γράφτηκε 6 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

 

[Samael]

καλησπερα σας παιδια... θελω να βρω μια παραγωγο

g(x)= f(2x+1)-2e^2x+1

g'(x) = ;;

g(0) = 0 επειδη η ασκηση λεει f(1) = 2e

Οι αρχικές συνθήκες είναι γενικά αδιάφορες όταν θέλουμε να παραγωγήσουμε .
Επίσης εφόσον δεν έχουμε τον τύπο της f αναλυτική έκφραση για την παράγωγο της g δεν μπορεί να βρεθεί αλλά το εξής γίνεται :

g'(x) = [f(2x+1) - 2e^(2x+1)]'
g'(x) = [f(2x+1)]' -2[e^(2x+1)]'
g'(x) = f'(2x+1)(2x+1)' - 2(2x+1)'e^(2x+1)
g'(x) = 2f'(2x+1) -4e^(2x+1)

Σύμφωνα με τον κανόνα της αλυσίδας .

Εαν είναι δυνατό θα βόλευε πολύ να έχουμε την πλήρη εκφώνηση μήπως υπάρχει περίπτωση να βρεθεί τελικά αναλυτικά η παράγωγος της g . Χωρίς να σημαίνει βέβαια αυτό οτι το ερώτημα ζητάει κάτι τέτοιο . Απλά επειδή έδωσες αρχικές συνθήκες , κάτι το οποίο γενικά όπως είπα δεν χρειάζεται στην παραγώγιση .

Σημείωση: Το μήνυμα αυτό γράφτηκε 6 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

 

[aekarare]

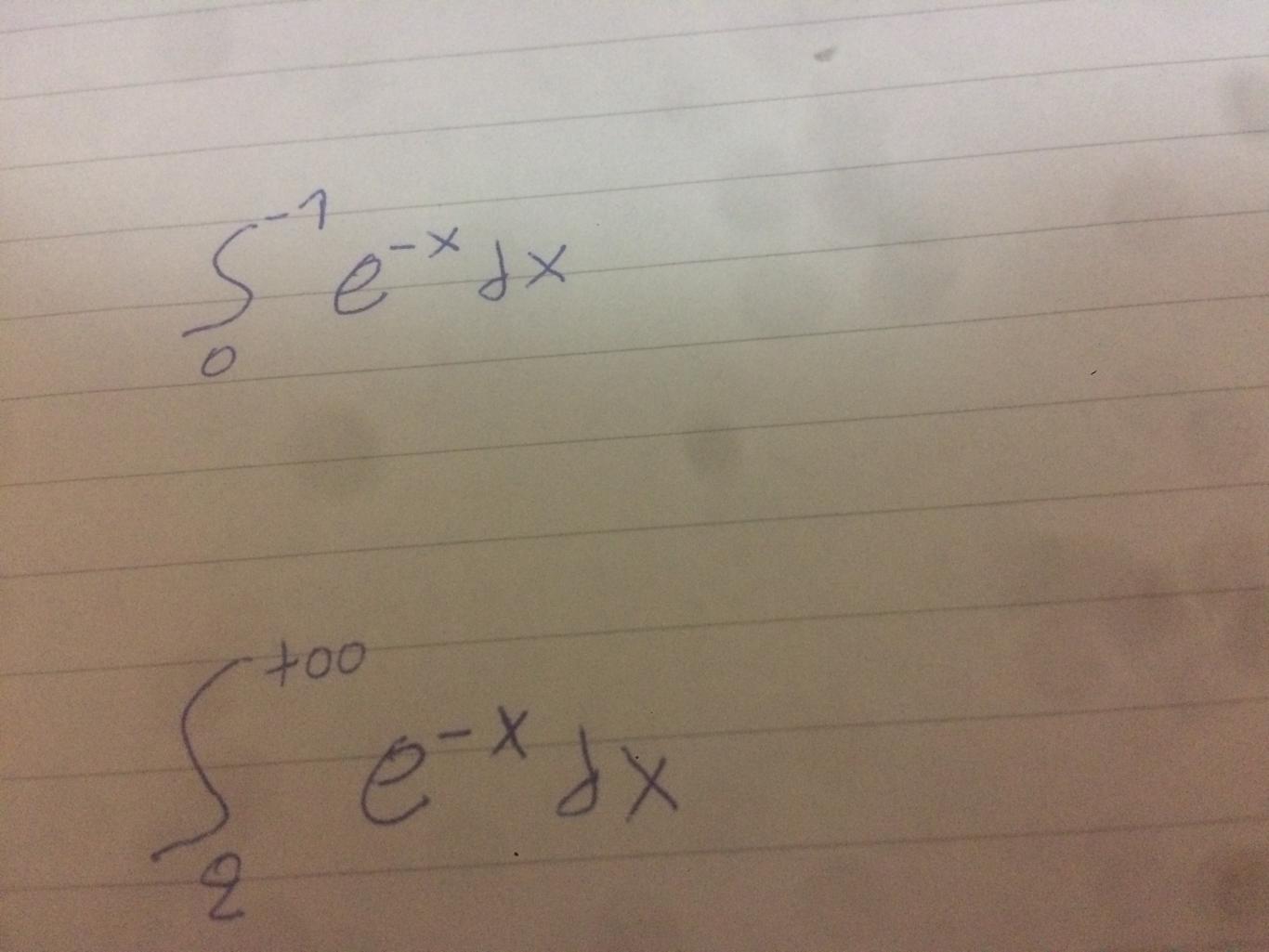
παιδια χρειαζομαι βοηθεια με τα παραπανω ολοκληρωματα..μπορει καποιος να μου γραψει αναλυτικα πως λυνονται??

Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

 

[Samael]

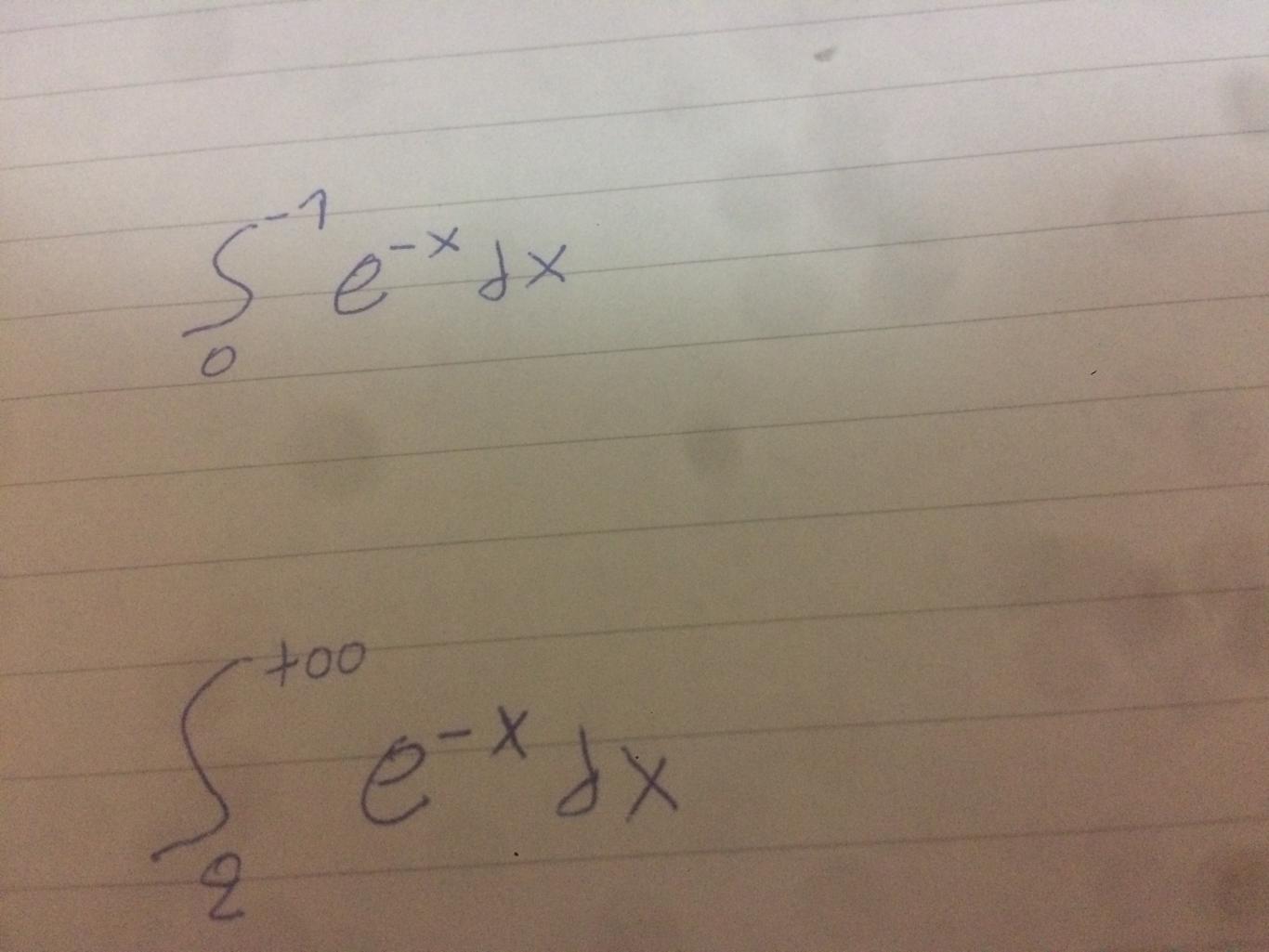
παιδια χρειαζομαι βοηθεια με τα παραπανω ολοκληρωματα..μπορει καποιος να μου γραψει αναλυτικα πως λυνονται??

Το πρώτο ολοκλήρωμα λύνεται όπως ξέρεις απο το λύκειο . Μπορείς να το λύσεις και έτσι,εαν δεν θυμάσαι όμως :

de^(-x)/dx = -e^(-x)

Αρα - de^(-x) = e^(-x) dx .
Παιρνόντας ολοκληρώματα απο 0 εως -1 αριστερά και δεξιά έχουμε :

( e^(-x) | για x = 0 και x = -1 ) = ( e^(-x) | για x = -1 και x = 1 )

Δεξιά προκύπτει η ζητούμενη παράσταση και αριστερά υπολογίζουμε αυτό που προέκυψε .

Ολοκλήρωμα του e^(-x) απο 0 εως -1 = e^(-0) - e^(-(-1)) = 1 - e .

Το δεύτερο ολοκλήρωμα τώρα . Αποτελεί γενικευμένο ολοκλήρωμα . Η αντιμετώπιση του δεν διαφέρει δραματικά . Απλά εδώ στα όρια παίρνεις 2 εως +οο και αριστερά υπολογίζεις :

e^(-2) - e^(-oo) = 1/e²

Άρα το ολοκλήρωμα απο το 2 εως το +οο του e^(-x) = 1/e² .

Φυσικά κάποια βήματα σε γενικές περιπτώσεις δεν μπορούν να εφαρμοστούν έτσι γιατί υπάρχει ο κίνδυνος η συνάρτηση να μην είναι συνεχής . Ωστόσο εδώ με γρήγορη εποπτεία μπορούμε να δούμε οτι αυτό δεν ήταν πρόβλημα . Και εννοείται οτι το ολοκλήρωμα μπορεί υπο άλλες περιπτώσεις να μην συγκλίνει . Ούτε αυτό συναντήσαμε όμως .

Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

 

[aekarare]

Το πρώτο ολοκλήρωμα λύνεται όπως ξέρεις απο το λύκειο . Μπορείς να το λύσεις και έτσι,εαν δεν θυμάσαι όμως :

de^(-x)/dx = -e^(-x)

Αρα - de^(-x) = e^(-x) dx .
Παιρνόντας ολοκληρώματα απο 0 εως -1 αριστερά και δεξιά έχουμε :

( e^(-x) | για x = 0 και x = -1 ) = ( e^(-x) | για x = -1 και x = 1 )

Δεξιά προκύπτει η ζητούμενη παράσταση και αριστερά υπολογίζουμε αυτό που προέκυψε .

Ολοκλήρωμα του e^(-x) απο 0 εως -1 = e^(-0) - e^(-(-1)) = 1 - e .

Το δεύτερο ολοκλήρωμα τώρα . Αποτελεί γενικευμένο ολοκλήρωμα . Η αντιμετώπιση του δεν διαφέρει δραματικά . Απλά εδώ στα όρια παίρνεις 2 εως +οο και αριστερά υπολογίζεις :

e^(-2) - e^(-oo) = 1/e²

Άρα το ολοκλήρωμα απο το 2 εως το +οο του e^(-x) = 1/e² .

Φυσικά κάποια βήματα σε γενικές περιπτώσεις δεν μπορούν να εφαρμοστούν έτσι γιατί υπάρχει ο κίνδυνος η συνάρτηση να μην είναι συνεχής . Ωστόσο εδώ με γρήγορη εποπτεία μπορούμε να δούμε οτι αυτό δεν ήταν πρόβλημα . Και εννοείται οτι το ολοκλήρωμα μπορεί υπο άλλες περιπτώσεις να μην συγκλίνει . Ούτε αυτό συναντήσαμε όμως .

Επειδη στο πανεπιστημιο τα καναμε αλλιως και δεν καταλαβαινω πως τα κανεις θα στειλω φωτο πως τα λυνω εγω και αν μπορεις πες μου που εχω λαθος

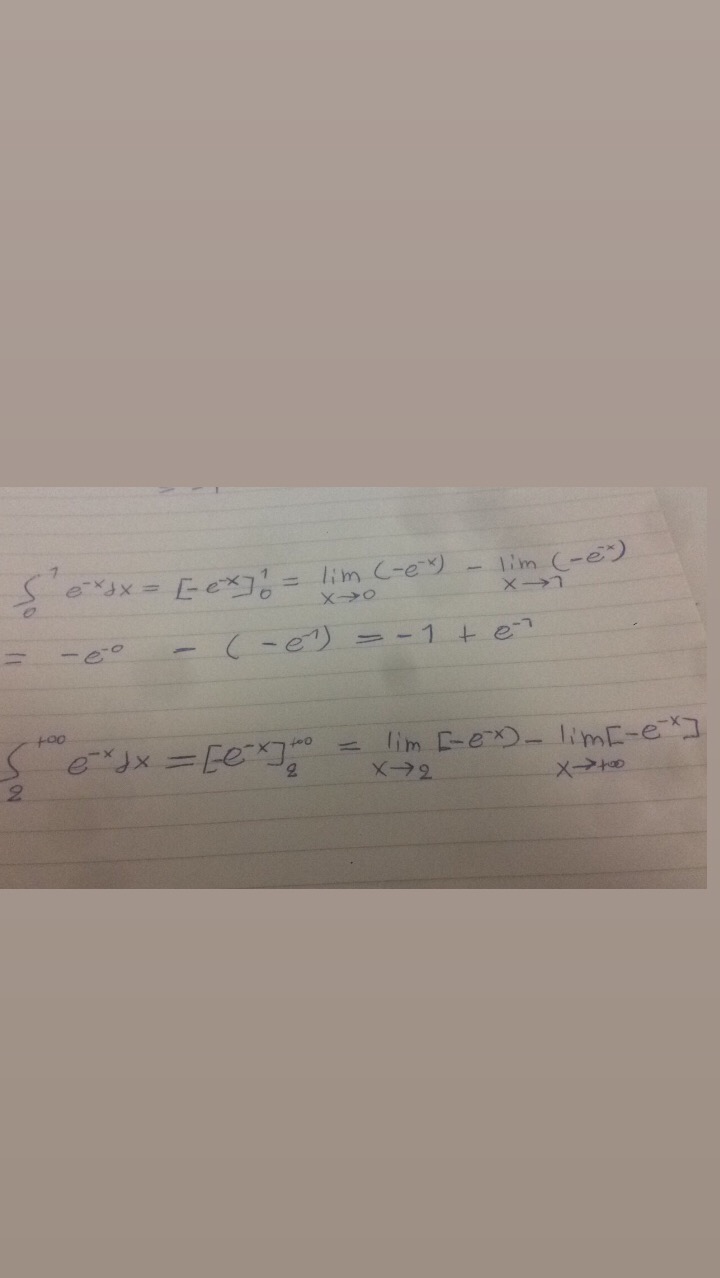
στο πρωτο σε τι εχω λαθος?..στο δευτερο ξερω να το παω μεχρι εκεινο το σημειο..ουσιαστικα κολλαω στο lim με το χ να τεινει στο + απειρο

νομιζω στο πρωτο βρηκα το λαθος μου..πρεπει απλα πρωτα να κανω το lim με το x τεινει στο 1 και μετα το lim με το x τεινει στο 0..τοτε βγαινει:-e^-1 +1 που ειναι και η σωστη απαντηση(επισης στην αρχη ειχα γραψει λαθος το πρωτο ολοκληρωμα ειναι 1 οχι -1)..τωρα απλα κολλαει στο δευτερο ολοκληρωμα γιατι δεν ξερω τι να κανω το lim με το + απειρο

Νομιζω βρηκα και την λυση του δευτερου..το e^-oo ισουται με 0;μαλλον εκει κολλουσα

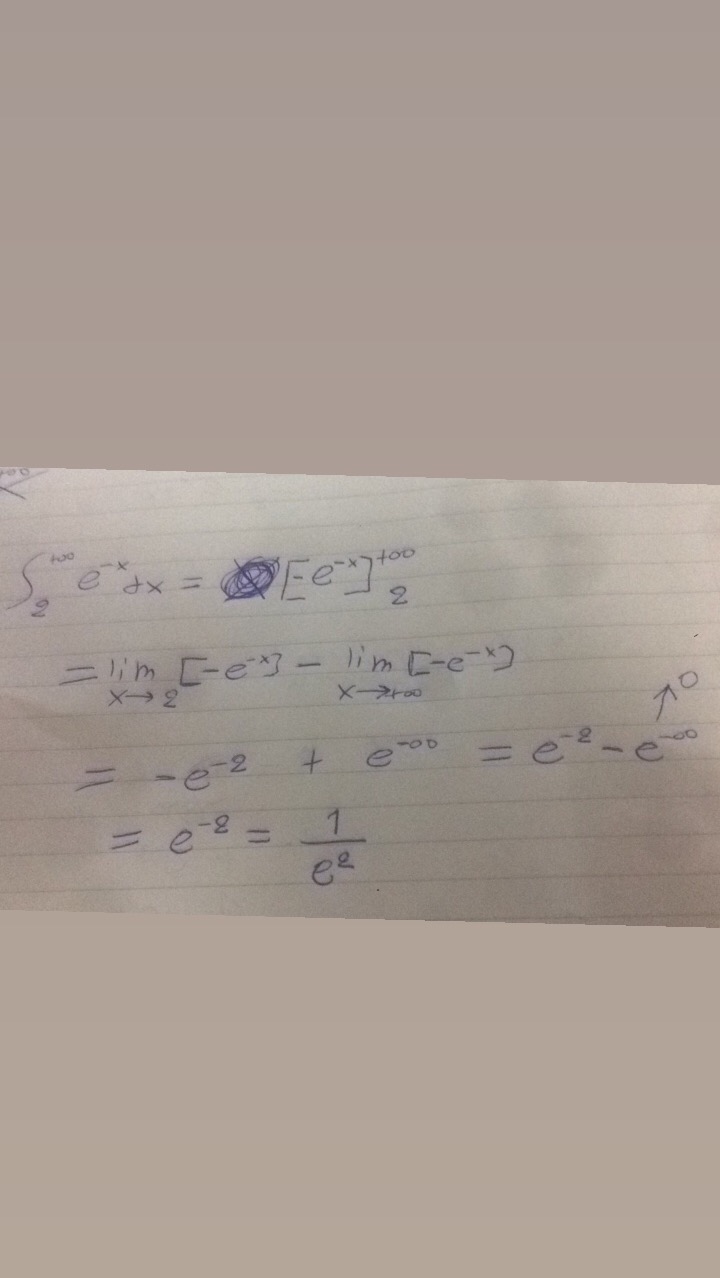
Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

 

[Samael]

νομιζω στο πρωτο βρηκα το λαθος μου..πρεπει απλα πρωτα να κανω το lim με το x τεινει στο 1 και μετα το lim με το x τεινει στο 0..τοτε βγαινει:-e^-1 +1 που ειναι και η σωστη απαντηση(επισης στην αρχη ειχα γραψει λαθος το πρωτο ολοκληρωμα ειναι 1 οχι -1)..τωρα απλα κολλαει στο δευτερο ολοκληρωμα γιατι δεν ξερω τι να κανω το lim με το + απειρο

Νομιζω βρηκα και την λυση του δευτερου..το e^-oo ισουται με 0;μαλλον εκει κολλουσα

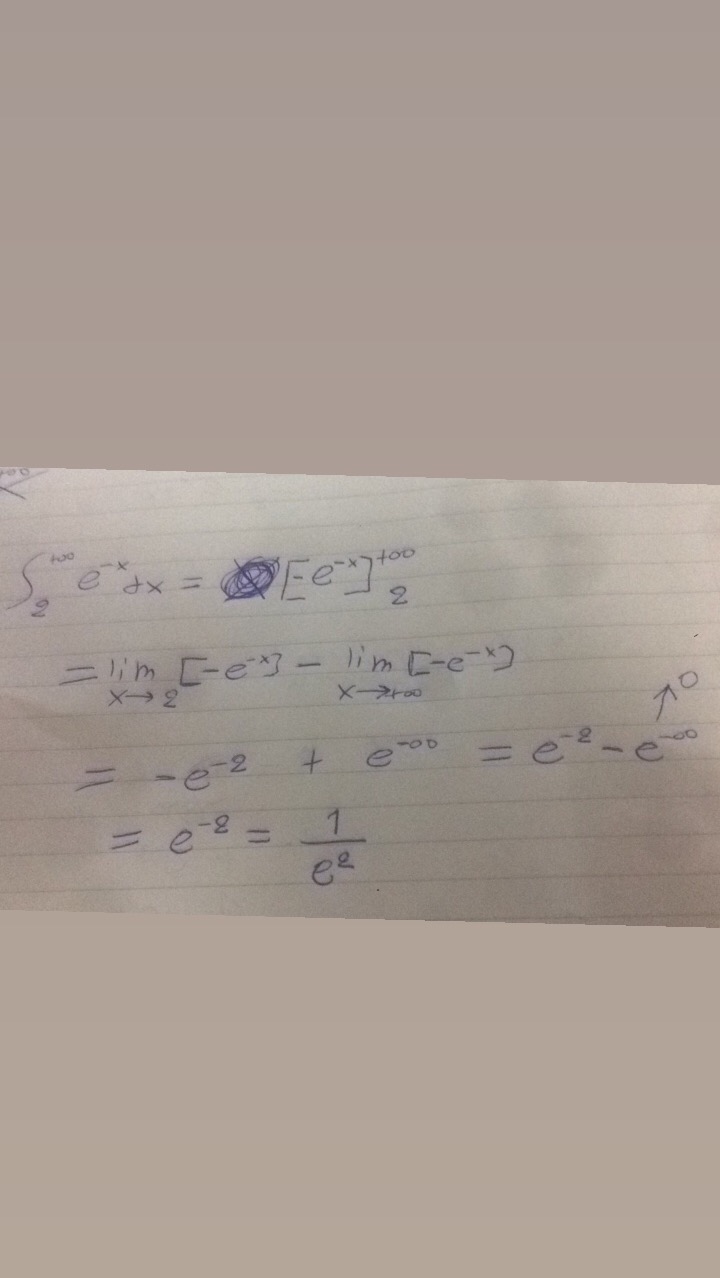
Είσαι σωστός τότε και στο πρώτο,εφόσον τελικά είναι 1 και όχι -1 και στο δεύτερο . Απλά στα γενικευμένα ολοκληρώματα δεν υπολογίζεις ακριβώς την συνάρτηση στο άπειρο ,αλλά παίρνεις το όριο της .Λογικά αυτό θα σε μπέρδευε . Όπως και εαν επιλέξεις να το δεις πάντως είσαι σωστός .

Ο τρόπος που το έλυσα αρχικά απαιτεί πολύ καλή εξοικείωση με τα διαφορικά . Γενικά δεν είναι απαραίτητο όμως για να κάνεις τις πράξεις . Εαν τυχόν κάποια στιγμή κάνεις ή το απαιτεί το πτυχίο σου, προχωρημένη μηχανική θα καταλάβεις όμως πόσο βοηθάει .

Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

 

[aekarare]

Είσαι σωστός τότε και στο πρώτο,εφόσον τελικά είναι 1 και όχι -1 και στο δεύτερο . Απλά στα γενικευμένα ολοκληρώματα δεν υπολογίζεις ακριβώς την συνάρτηση στο άπειρο ,αλλά παίρνεις το όριο της .Λογικά αυτό θα σε μπέρδευε . Όπως και εαν επιλέξεις να το δεις πάντως είσαι σωστός .

Ο τρόπος που το έλυσα αρχικά απαιτεί πολύ καλή εξοικείωση με τα διαφορικά . Γενικά δεν είναι απαραίτητο όμως για να κάνεις τις πράξεις . Εαν τυχόν κάποια στιγμή κάνεις ή το απαιτεί το πτυχίο σου, προχωρημένη μηχανική θα καταλάβεις όμως πόσο βοηθάει .

ειμουν απο βιολογια και αυτα τα λιγα ολοκληρωματα θα μου χρειαστουν στις πιθανοτητες..το αλλο εξαμηνο θα κανω ολοκληρωματα στα μαθηματικα..οποτε για αυτο εχω μια δυσκολια..ευχαριστω πολυ

Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

 

[Samael]

ειμουν απο βιολογια και αυτα τα λιγα ολοκληρωματα θα μου χρειαστουν στις πιθανοτητες..το αλλο εξαμηνο θα κανω ολοκληρωματα στα μαθηματικα..οποτε για αυτο εχω μια δυσκολια..ευχαριστω πολυ

Κατάλαβα ,λογικό τότε !
Διάβασε και δεν θα έχεις πρόβλημα . Να ξέρεις πάντως οτι ο διαφορικός και ολοκληρωτικός λογισμός είναι όψεις του ίδιου νομίσματος . Μάθε και τα δύο κεφάλαια πολύ καλά .

Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

 

[aekarare]

Είναι η εξίσωση 3x+5/x^2+ax+9 και λέει να βρεθούν οι τιμές του α για τις οποίες η εξίσωση έχει πεδίο ορισμού όλο το R..Πως δουλεύουμε σε μια τέτοια άσκηση?

Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

 

[Guest 749981]

Εννοείς μήπως (3χ + 5)/(χ^2+αχ+9);
Αν ναι, τότε το τριώνυμο δεν πρέπει να μηδενίζεται,
άρα Δ < 0
<=> α^2 - 4*1*9 < 0
<=> -6 < α < 6.

Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

 

[aekarare]

γιατί έτσι όμως; αφού άμα λύσουμε το a^2-36<0..Θα είναι a^26..a<+-6

Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

 

[Guest 749981]

γιατί έτσι όμως; αφού άμα λύσουμε το a^2-36<0..Θα είναι a^2< 36..a<+-6

Είναι δευτεροβάθμια ανίσωση και δε λύνεται τόσο άμεσα όσο η εξίσωση. Το α<±6 δεν υφίσταται. Αφού βρεις τις ρίζες της αντίστοιχης εξίσωσης κάνεις τον πίνακα προσήμου.

Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

 

[aekarare]

Καλημέρα παιδιά..ειναι μια άσκηση που δίνει την εξίσωση x^2-3x+2 και λεει να γίνει η μελέτη της..παιρνω την πρώτη παραγωγό(f(x)=2x-3) και βρίσκω μονοτονία και ακροοτατα..Πάω μετά να βρω κυρτοτητα από την 2η παραγωγο..Αλλά η δεύτερη παραγωγός είναι f"(x)=2..Πρέπει απλά να γράψω στην άσκηση ότι αφού η παραγωγός είναι θετική παντού τότε τα κοιλα είναι παντού προς τα πάνω;(για να απαντησω για την κυρτοτητα)

Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

 

[Μάρκος Βασίλης]

Καλημέρα παιδιά..ειναι μια άσκηση που δίνει την εξίσωση x^2-3x+2 και λεει να γίνει η μελέτη της..παιρνω την πρώτη παραγωγό(f(x)=2x-3) και βρίσκω μονοτονία και ακροοτατα..Πάω μετά να βρω κυρτοτητα από την 2η παραγωγο..Αλλά η δεύτερη παραγωγός είναι f"(x)=2..Πρέπει απλά να γράψω στην άσκηση ότι αφού η παραγωγός είναι θετική παντού τότε τα κοιλα είναι παντού προς τα πάνω;(για να απαντησω για την κυρτοτητα)

Ναι, αυτό εννοεί, αλλά:

1. Δε δίνεται μία «εξίσωση», αλλά μία «συνάρτηση»/ένα «τριώνυμο» κ.λπ.. Προσοχή με την ορολογία!
2. Δε χρειάζεται να πάρουμε τόσο βαρβάτα εργαλεία για να μελετήσουμε ένα τριώνυμο. Από την Α' λυκείου, γνωρίζουμε πού παρουσιάζει ένα τριώνυμο ακρότατα, ποιες είναι οι ρίζες του, ποια είναι η μονοτονία του και πότε στρέφει τα κοίλα άνω/κάτω. Μπορείς να τα ξαναθυμηθείς από εδώ.

Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

 

[Guest 749981]

Μου θύμισε το θέμα που ρώτησε ο φίλος τις προάλλες. Νομίζω εύκολη και γρήγορη άσκηση, αλλά η παγίδα που έκρυβε κόστισε.

Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.