FROM SPACE
Νεοφερμένος


Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Άρα η εξίσωση της εφαπτομένης είναι
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
*Serena*
Τιμώμενο Μέλος


1) Δινεται η εξισωση χ^2 +ψ^2 + ριζα 4-λ^2*χ +λψ=0 με απολυτο λ μικροτερο η ισο του 2.
- δειξτε οτι η εξισωση παριστανει κυκλο για καθε λ που διερχεται απο την αρχη των αξονων
- βρειτε συναρτησει του λ τις συντεταγμενες του κεντρου του κυκλου
- βρειτε το γεωμετρικο τοπο των κεντρων των κυκλων αυτων οταν το λ μεταβαλλεται
- αν Α,Β ειναι η τομη του αρχικου κυκλου με την ευθεια ψ=χ-2 υπολογιστε το λ ωστε να ισχυει ΟΑ*ΟΒ=0
- να βρειτε τισ εξισωσεις των εφαπτομενων του κυκλου που διερχονται απο το Μ.
- αν Α,Β ειναι τα σημεια επαφης των παραπανω εφαπτομενων με τον κυκλο, να βρειτε το εμβαδονξ του τριγωνου ΜΑΒ.

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
vimaproto
Πολύ δραστήριο μέλος


Πολλή δουλειάΜηπως μπορει καποιος να με βοηθησει σε δυο ασκησεις:
1) Δινεται η εξισωση χ^2 +ψ^2 + ριζα 4-λ^2*χ +λψ=0 με απολυτο λ μικροτερο η ισο του 2.
2) Δινεται η εξισωση χ^2 +ψ^2-4χ+2ψ+3=0 και το σημειο Μ(2,1) με κεντρο το Κ(2,-1) και ακτινα ριζα 2.
- δειξτε οτι η εξισωση παριστανει κυκλο για καθε λ που διερχεται απο την αρχη των αξονων
- βρειτε συναρτησει του λ τις συντεταγμενες του κεντρου του κυκλου
- βρειτε το γεωμετρικο τοπο των κεντρων των κυκλων αυτων οταν το λ μεταβαλλεται
- αν Α,Β ειναι η τομη του αρχικου κυκλου με την ευθεια ψ=χ-2 υπολογιστε το λ ωστε να ισχυει ΟΑ*ΟΒ=0
- να βρειτε τισ εξισωσεις των εφαπτομενων του κυκλου που διερχονται απο το Μ.
- αν Α,Β ειναι τα σημεια επαφης των παραπανω εφαπτομενων με τον κυκλο, να βρειτε το εμβαδονξ του τριγωνου ΜΑΒ.

Ασκηση 2
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Συνημμένα
vimaproto
Πολύ δραστήριο μέλος
paladin_k20
Εκκολαπτόμενο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
vimaproto
Πολύ δραστήριο μέλος


Αν ζητάς τη λύση:Nα υπολογιστει το ολοκληρωμα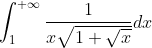
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Συνημμένα
paladin_k20
Εκκολαπτόμενο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
akis95
Δραστήριο μέλος


Βρειτε τον γτ των σημειων Μ απο τα οποια διερχεται μια μονο ευθεια που οριζεται απο την (1)
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
vimaproto
Πολύ δραστήριο μέλος


Δεν ξέρω αν ο συλλογισμός μου είναι σωστός, αλλά νομίζω πως αυτό ισχύει για μία μόνο τιμή του λ. Γράφω την παράσταση σαν τριώνυμο του λ που έχει (πρέπει) διακρίνουσα =0 Άρα χλ²-χ+2yλ+2=0 ===> χλ²+2yλ-χ+2=0 και 4y²-4χ(-χ+2)=0 ===. χ²-2χ+1+y²=1 ==> (χ-1)²+y²=1 Ο Γ.Τ. είναι κύκλος με κέντρο το σημείο (1,0) και ακτίνα ρ=1εστω (λ²-1)χ+2λy+2=0(1) για καθε λ ανηκει στο R
Βρειτε τον γτ των σημειων Μ απο τα οποια διερχεται μια μονο ευθεια που οριζεται απο την (1)
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
loukas(^_^)
Νεοφερμένος


Να βρεθει ο γεωμετρικος τοπος των σημειων Μ(χ,y) του επιπεδου για τα οποια ισχυει : x(στη τριτη) + y(στην τριτη) + x(τετραγωνο)*y + x*y(τετραγωνο) =x+y
*=(επι)
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
tebelis13
Πολύ δραστήριο μέλος


μπορει να με βοηθησει κανενας??
Να βρεθει ο γεωμετρικος τοπος των σημειων Μ(χ,y) του επιπεδου για τα οποια ισχυει : x(στη τριτη) + y(στην τριτη) + x(τετραγωνο)*y + x*y(τετραγωνο) =x+y
*=(επι)
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
loukas(^_^)
Νεοφερμένος


Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
dimitra..roxy
Νεοφερμένος



1) Σε ενα τριγωνο τριπλασιαζουμε τη βαση και διπλασιαζουμε το υψος. πως θα μεταβληθει το εμβαδον?
2) Το γινομενο δυο πλευρων τριγωνου ειναι διπλασιο του εμβαδου. να βρεθει η περιεχομενη γωνια των πλευρων.
οποιος μπορει ας με βοηθησει με τις παραπανω ασκησεις

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


ii) Απλή εφαρμογή του τύπου
Προσπάθησέ το κι αν δεν μπορείς ξαναστείλε
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
maria98125
Νεοφερμένος


Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
vimaproto
Πολύ δραστήριο μέλος


Κάτω δεξιά [Περισσότερες επιλογές μορφοποίησης] και μετά κάτω αριστερά [Σύνταξη κώδικα Latex]Πώς χρησιμοποιούμε κώδικα latex?
Στον πίνακα που εμφανίζεται , αφού γράψεις αυτά που θέλεις, πατάς "προεπισκόπηση" αν έχεις κάνει κάποια λάθη τα διορθώνεις και όταν το δεις σωστό το κάνεις copy. Γυρίζεις στο κείμενό σου και το κάνεις paste. Ομοίως για νέα εργασία.
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
maria98125
Νεοφερμένος


Και δεν μπορώ να πατήσω εκεί που λέει αντιγραφή στο πρόχειρο...
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
paladin_k20
Εκκολαπτόμενο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
- Status
- Το θέμα δεν είναι ανοιχτό για νέες απαντήσεις.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 2 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 23 μέλη διάβασαν αυτό το θέμα:
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Chat
Chat
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki




